纹理特征
纹理是指存在于图像中某一范围内的形状很小的、半周期性或有规律地排列的图案。在图像判读中使用纹理表示图像的均匀、细致、粗糙等现象。纹理是图像处理和模式识别的主要特征之一。纹理特征是指图像灰度等级的变化,这种变化是与空间统计相关的。图像的纹理特征反应了图像本身的属性,有助于图像的区分。一般的图片都具有丰富、稳定的纹理特征,且利用统计方法方法提取图像的纹理特征具有计算量小的特点。
a.统计法
a)灰度共生矩阵
假定,在一幅图像中规定了一个方向(水平的、垂直的等)和一个距离(一个象素,两个象素等)。那么该物体的共生矩阵P的第(i,j)个元素值等于灰度级i和j在物体内沿该方向相距该指定距离的两个像素上同时出现的次数,除以M,其中M是对P有贡献的像素对的总数。矩阵P是N×N的,其中N为灰度阴影级的划分数目。
各个共生矩阵可以通过对距离和方向的各个组合来定义。对矩阵有贡献的像素对的总数M,比物体内部像素的个数少,而且这个数目随着距离的增加逐渐减少。因此,小物体的矩阵会相当稀疏。由于这个原因,灰度级划分N常常被减少,例如从256级到8级,以便于共生矩阵的计算。
在水平方向上的共生矩阵,如果考虑当前像素的左右方向上的像素,则称为对称共生矩阵,如果只考虑当前像素的右或左方向上的像素,则称为非对称共生矩阵。
例如,设一幅图像的大小为M×N,灰度级为L,G={0,1,2……., L-1},f(x,y)是坐标(x,y)处像素的灰度级,一幅图像的一个共生矩阵是一个L×L矩阵 ,T中的元素是图像灰度的空间关系,以及按特定方式表示的两灰度间变化的次数。
,T中的元素是图像灰度的空间关系,以及按特定方式表示的两灰度间变化的次数。
我们只考虑水平方向的共生矩阵,则对称共生矩阵的定义如下:
 (3-2)
(3-2)
式中

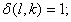 (3-3)
(3-3)
否则 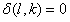 (3-4)
(3-4)
当只考虑水平方向的右边的像素,则非对称共生矩阵的定义如下:
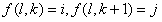
 (3-5)
(3-5)
否则  (3-6)
(3-6)
我们得到从灰度级i到j变化的概率如下:
 (3-7)
(3-7)
b) Tamura
Tamura以人类的主观心理度量作为标准,提出了六个基本的纹理特征,这些特征包括:粗糙度(coarseness),对比度(contrast),方向度(directionality),线像度(linelikeness),规整度(regularity)和粗略度(roughness),这些特征中最重要的主要是纹理的粗糙度,对比度和方向度。这些纹理特征很好的对应了人类视觉感知,在许多图像检索系统中得到应用。这里主要介绍一下粗糙度,对比度和方向度的计算。
l 粗糙度
1)计算移动平均数(moving average),对于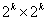 的窗口,移动平均数为:
的窗口,移动平均数为:
 (3-8)
(3-8)
2)计算水平和垂直向的偏差

 (3-9)
(3-9)
3)确定窗口大小
 (3-10)
(3-10)
4)计算平均窗口大小
 (3-11)
(3-11)
l 对比度
对比度描述图像的明亮程度,它受黑白色或者不同的灰度阴影的影响,使用下面的等式来计算对比度:
 (3-12)
(3-12)
黑白色的偏差为:
 (3-13)
(3-13)
l 方向度
方向性是指图像里灰度值的方向。计算方向性需要以下四步:
1)计算每个像素的梯度g。梯度指此像素点周围灰度值增加最快的方向。水平梯度△h等于左边像素的三个灰度值与右边像素的三个灰度值之间的偏差,而垂直梯度△v则是上下像素的三个灰度值偏差。

 (3-14)
(3-14)
2)计算梯度向量的极坐标
 (3-15)
(3-15)
3)计算倾斜向量角度的直方图
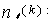 表示满足
表示满足 和
和  条件的像素点的比例。
条件的像素点的比例。
4)得到直方图以后,计算波峰(波谷到波谷)周围的值的变化总和
方向性 = 波谷到波谷之间变化的总合
本文用粗糙度和对比度作为Tamura特征对SAR图像提取特征。
3.1.3 滤波器
频谱方法的典型是对图像进行傅立叶变换,从傅立叶频谱成分的分布中来求得纹理特征。频谱分析技术是用于区域自相关函数或傅立叶变化域的能量分布来检测纹理的周期,包括计算峰值处的面积、峰值处的相位、峰值与原点的距离平方、两个峰值之间的相角差等手段。
应用频谱法提取图像的纹理特征,实际上是将纹理基元(texton)及其在图像区域中的不同形式出现的“副本”用在不同尺度和方向上的子波能量分布表示出来。本文采用Gabor滤波器[6]为基础的多分辨率分析进行纹理图像特征提取,使用这种纹理特征是基于一下考虑:
(1). 在信号处理技术领域中,Gabor是被公认信号表示尤其是图像辨识的最好方法之一。
(2). 从心理学的角度,人类辨识同类纹理是同时依赖于形状相似性(即空间属性)和组织结构相似性(即频域属性)的,这就要求在一种能同时对空域和频域进行有效的描述方法。Gabor变换已被证明是在二维测不准情况下,对信号空间域和频率域的最佳描述。
(3). 生物学领域的研究也发现,二维Gabor滤波器能很好的描述哺乳动物大脑初级视觉皮层部分的简单细胞可接收信息域的分布,两者在空间域均有相似的局部特点,这与人类视觉系统也是一致的。
(4). Gabor滤波器可以被视为方向和尺度均可以变化的边缘和直线(条纹)的检测器,并且,对于一个给定区域中的这些微观特征的统计,可以用来表示基本的纹理信息。
(5). 大量的实验结果表明,在各种小波变换形式中,Gabor小波变换的检索效果最好。
a)Gabor小波函数
由于局域化的频率描述需要一个在空间域中固定宽度的“窗”,则频域带宽也就被固定在一个定长的尺度上。所以局域化的频率描述还不能够完全适合于特征描述。为了优化能检测不同尺度下的局部特征,就需要不同尺度的滤波器,而不是一个固定大小的滤波器。
因此,采用基小波为Gabor函数的小波变换来提取纹理特征。二维Gaobr函数gabor可以表示为:
 (3-16)
(3-16)
其中,W是高斯函数复调制频率。Gabor函数的实部和虚部如图2


(a)实部 (b)虚部
图2 Gabor函数的实部和虚部
则g(x,y)的Fourier变换G(u,v)为:
 (3-17)
(3-17)
其中, ,
,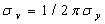 。
。
使用g(x,y)作为母函数,通过对g(x,y)进行适度尺度扩张和旋转变换,可以得到一组自相似的滤波器,即为Gabor小波:
 (3-18)
(3-18)
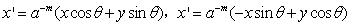 (3-19)
(3-19)
式中,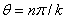 ,且k是方向的数目,m和n分别表示相应的尺度和方向
,且k是方向的数目,m和n分别表示相应的尺度和方向 ,式子(3-20)中的尺度因子
,式子(3-20)中的尺度因子  保证能量大小与m无关。根据傅立叶变换的线性特性,有
保证能量大小与m无关。根据傅立叶变换的线性特性,有
 (3-21)
(3-21)
通过改变m和n的值,就可以得到一组尺度和方向都不相同的滤波器。
b)Gabor滤波器组
由于Gabor小波集的非正交性,使得滤波后的图像中会有冗余信息。为剔除这些冗余信息,让 和
和 分别表示所研究频域中最低和最高的频率值,比如最粗糙尺度滤波和最佳尺度滤波的中心频率,
分别表示所研究频域中最低和最高的频率值,比如最粗糙尺度滤波和最佳尺度滤波的中心频率, 为多分辨率分解的尺度数,滤波器的基本设计策略是保证Gabor滤波器组的响应在频率的上半峰幅值可以相互接触但又不相互重叠,如图3所示,方向数和尺度数9和4。
为多分辨率分解的尺度数,滤波器的基本设计策略是保证Gabor滤波器组的响应在频率的上半峰幅值可以相互接触但又不相互重叠,如图3所示,方向数和尺度数9和4。

图3 Gabor滤波器中相应的半峰幅值的周期
由于滤波器的尺度间隔是指数级的,可得 ,则尺度参数为:
,则尺度参数为:
 (3-22)
(3-22)
滤波器参数 和
和 (即
(即 和
和 )的计算如下:
)的计算如下:
一方面,如图t表示最小滤波的半幅宽度,则可得到:
 (3-23)
(3-23)
因为标准方差为 的高斯半幅值为
的高斯半幅值为 ,那么这里最大滤波的半幅值应该为
,那么这里最大滤波的半幅值应该为 。
。
由上面的式(3-22)和(3-23)可得:
 (3-24)
(3-24)
另一方面,两相邻椭圆切线角度为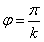 ,k是方向数,可得:
,k是方向数,可得:
 (3-25)
(3-25)
设 ,则有
,则有
 (3-26)
(3-26)
对于式(3-26)这个以u为变量的二次方程,其有实数解的实例的条件为:
 (3-27)
(3-27)
综合式子(3-27)和(3-24)可得:
 (3-28)
(3-28)
为了消除亮度值大小的影响,可以给二维Gabor滤波器的实部加上一个常量,使得它的均值为零(即设式(3-17)中G(0,0)=0)。
本文选取Uh=0.4和Ul=0.1,3个尺度,每个尺度分别为8、8、4,对每幅图像滤波后开4*4个窗口,计算每个窗口的均值,做为最后的gabor特征矢量。
纹理特征提取中最重要的部分是滤波器或滤波器组的选择,以下是各类滤波器方案。
l 启发式设计滤波器组
对大多数滤波方法的基本假设就是,频域的能量分布可以确定一种纹理。因此,如果将纹理图像的频谱分解为足够多数量的子带,不同纹理的谱能量信号就不相同。利用这个提出了一些滤波器组方法与方案。
Law Filter 掩模
纹理识别滤波的第一个方法由Laws提出,建议使用一组可分离的滤波器组,每一维5个,总共25个。推荐的滤波器掩模是
环形和楔形滤波器
假定纹理可以被空间频率和方向区分开。为提取特征使用七个双向环形滤波器和四个楔形方向滤波器。滤波器设计在二维空间频域内。
双向Gabor滤波器组
双向Gabor滤波器组是高斯形状的带通滤波器,双向覆盖半径空间频率范围和多个方向。这个方法是根据早期哺乳动物的视觉模型推出的,滤波器在时域和频域有最佳清晰度。
方向为0°的基本偶对称Gabor滤波器是带通滤波器,单位冲击响应为:
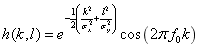 (3-29)
(3-29)
 表示半径中心频率。其他方向可以通过旋转相关坐标系(k,l)来获得。此滤波器有无限单位冲激响应,但实际实验中近似为有限长度滤波器。
表示半径中心频率。其他方向可以通过旋转相关坐标系(k,l)来获得。此滤波器有无限单位冲激响应,但实际实验中近似为有限长度滤波器。
对256*256大小的图像,提供五个半径频率和四个方向。这里所做的测试中不考虑输入图像的大小,使用的是相同数目的滤波器。离散半径中心频率为 方向为0°45°90°135°。
方向为0°45°90°135°。
Wavelet transform, Packets and Frames
像离散小波变换这样的变换对应于特殊滤波参数和子带分解的临界采样滤波器组。因此小波变换方法就是滤波器组方法。离散小波变换和离散小波信息包变换都是临界采样多抽样率滤波器组。但是临界采样滤波器组暗含着不精确的纹理边缘。超完备小波表达的使用,即小波框架可以用来减轻这个问题。
离散余弦变换(DCT)
图像变换等价于临界采样滤波器组。以上方法在滤波器组中进行测试,但是不进行临界采样。由于一维的滤波掩模为 ,滤波器组是可分离的。
,滤波器组是可分离的。
正交镜像滤波器(QMF)
使用QMF做纹理分析。这就像小波滤波器类,是非常宽泛的一个滤波器的种类,它将无限冲击响应(IIR)和有限冲击响应(FIR)滤波器合并起来。
l 最优滤波器和滤波器组
启发式设计滤波器组在很多的实例中获得成功。但是,大部分的启发式设计滤波器组都暗含了大量的特征。因此,在特征提取和分类中的计算复杂度非常大。最优化滤波器或滤波器组可以产生低的特征维度,最大的特征分离以及一些情况下更简单的分类器。
一些最优化的方法会受限于两种纹理的问题,而其他的可适用于多种纹理问题。此外,一些方法只产生一个滤波器,其他的产生滤波器组。但是对所有方法都适用的是滤波器是根据一些纹理分类任务的相关标准进行优化的。
特征滤波器
使用纹理自相关函数衍生出的特征滤波器。对每一个纹理
 (3-30)
(3-30)
这里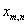 是图像,
是图像, 是求期望,计算特征向量和特征值。每个9*1的特征向量都对应于一个3*3的滤波器掩模。因此图像被对应于主特征向量的3*3滤波器所滤波。一组滤波器作用于一个纹理,所有的滤波器应用于合成图像。
是求期望,计算特征向量和特征值。每个9*1的特征向量都对应于一个3*3的滤波器掩模。因此图像被对应于主特征向量的3*3滤波器所滤波。一组滤波器作用于一个纹理,所有的滤波器应用于合成图像。
在原始的方法中,选取的是对应于加起来和达到至少总的特征值和的99%的特征值的滤波器。这就导致滤波器数量的庞大,每个纹理对应了5到9个的数量,在特征提取和分类系统中也就造成很大的计算复杂度。因此,滤波器的总数被限制为每种纹理最大为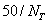 ,
,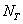 是纹理的数量。那么任何图像的滤波器最大数量也就是50。
是纹理的数量。那么任何图像的滤波器最大数量也就是50。
预测误差滤波器
这种滤波器给出每种纹理的最小二乘预测方差,因此滤波器的数量和纹理的数量相同。图像处理中的线性预测器是如下形式的方程 ,通过使用系数
,通过使用系数 ,根据领域N中的邻近像素来预测像素值。滤波器是通过使
,根据领域N中的邻近像素来预测像素值。滤波器是通过使 最小来完成优化的。纹理的最小二乘误差(LSE)预测器将会产生在二乘误差意义上的纹理和预测器输出之间的最大相似度。
最小来完成优化的。纹理的最小二乘误差(LSE)预测器将会产生在二乘误差意义上的纹理和预测器输出之间的最大相似度。
一般说来,不同纹理的LSE预测器也不相同。因此,对任何纹理,产生最小均值误差能量的预测器就是对应此纹理的预测器。由于产生最小局部预测误差能量的预测器对应于当下的纹理,这可以应用于分类。
最优表达的Gabor滤波器组
为了使得滤波器和当前纹理的特性相一致,使用窄带滤波器。滤波器的中心频率调到纹理的谱极点处。也就是说,对每一种纹理,相应的Gabor滤波器的中心频率选定为这种纹理的主要谱极点对应频率。建议使用手动程序来决定谱极点。不过,这个程序应该很容易扩展为全自动程序,手动程序对每个纹理选择两个滤波器来执行。平滑滤波器通过选定的滤波器的中心频率来确定。
由于这个方法也是关于图像表达的优化,因此不保证能很好分离特征。
最优两类Gabor滤波器
这个方案用来解决包含两种纹理的分类问题。Gabor滤波器中心频率给出产生最小模板分类错误的特征。评估大范围的中心频率(使用傅立叶变换)之后选取最佳来确定最优中心频率。用户需要选取滤波器带宽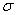 。评估
。评估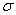 为2,4,8和16的Gabor滤波器,这些
为2,4,8和16的Gabor滤波器,这些 值是由Weldon et al.[15]提出的。平滑高斯滤波器空间宽度
值是由Weldon et al.[15]提出的。平滑高斯滤波器空间宽度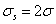 。
。
这个滤波设计方法是基于阈值分类器对特征图像进行分类的。这样简单的分类器设计和使用起来都不复杂。此外,大量的参数更多的训练数据向量,因此阈值分类器只有一个参数,对训练数据的需求量也相对较低。
最优多类Gabor滤波器组
之前的优化滤波器设计方法只局限于一个滤波器两种纹理的问题。滤波器的带宽也是启发式决定的。此种Gabor滤波器组设计来解决包含任意数量纹理的问题。用户只需要选择用到的滤波器数量。Dunn and Higgins提出了基于特征提取模型的算法。但是使用了一个改进的准则函数,结合了滤波器尺寸和边缘准确性的影响。这个方法允许了多于两种纹理和多于一个滤波器。
评估许多的滤波器尺寸,选定最佳的来决定滤波器尺寸。在滤波器组中不同的滤波器有不同的尺寸。这些实验中用到的 。
。
最优两种纹理FIR滤波器
Gabor滤波器是高斯带通滤波器。这种滤波器唯一需要确定的参数就是半中心频率,方向和带宽。如果允许更多不定参数,就可以使滤波器更好的适应当前的纹理。最优两种纹理FIR滤波器产生在提取特征均值中具有最大比例的FIR滤波器。即最大化 标准来设计滤波器,
标准来设计滤波器, 是纹理i的特征均值。
是纹理i的特征均值。
Randen and Husoy认为这个标准对一些纹理对来说还不足够,发展了一个允许其他标准函数的更优方案。标准优化为
 以及
以及  (3-31)
(3-31)
 是特征方差。
是特征方差。
滤波器掩模的大小对结果也很重要。在精确边缘定位时,所支持的对称区域直观优先。为了得到支持的对称区域,需要奇数数量的掩模。初步的实验表明,对给定的分辨率,5*5或更大的掩模就足够了。一些纹理对需要比5*5更大尺寸的掩模。
最优FIR滤波器组
相关于标准函数 和
和 的FIR两种纹理的优化被扩展为多种纹理多个滤波器的解决方案。这个解决方案是基于一个滤波器分离不同组的纹理,然后的滤波器启发式分离一组中的纹理。
的FIR两种纹理的优化被扩展为多种纹理多个滤波器的解决方案。这个解决方案是基于一个滤波器分离不同组的纹理,然后的滤波器启发式分离一组中的纹理。
l 旋转不变滤波器
LM滤波器组
Leung-Malik(LM)集: 包含48个滤波器, 在6个方向,3个尺度和2个相位的高斯二次导组成了36个滤波器; 8个 高斯拉普拉斯滤波器; 4个高斯. 滤波器的尺度范围为: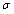 =1到
=1到 =10.
=10.

图4 LM滤波器组
S滤波器组
Schmid(S)集: 包含13个旋转不变形式:
 (3-32)
(3-32)
F0是为了获得一个0DC成分.其中( )取值为(2,1),(4,1),(4,2),(6,1),(6,2),(6,3),(8,1),(8,2),(8,3),(10,1),(10,2),(10,3),(10,4).所有的滤波器都具有旋转对称性.
)取值为(2,1),(4,1),(4,2),(6,1),(6,2),(6,3),(8,1),(8,2),(8,3),(10,1),(10,2),(10,3),(10,4).所有的滤波器都具有旋转对称性.

图5 S滤波器组
MR滤波器组
MR8滤波器组包含38个滤波器但是只有8种滤波器响应. 在所有的方向上记录最大响应保证旋转不变性. oriented edge和bar filtes在3个尺度上.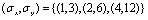 .
.
MR4是MR8的子集, oriented edge和bar filter 只取单个固定的尺度.
引入这些MR滤波器组的动机有两方面.第一是克服传统旋转不变滤波器不同提供较好的各向异性纹理的好特征的局限.另外,MR组还记录了最大响应的角度信息.使得我们可以计算相位间高阶相关统计信息.第二是滤波器响应空间的低维性.

图6 MR滤波器组



