实现三维模型的网格简化算法研究

0  引言

随着科学技术的进步，在计算机图形学、虚拟现实、地理信息系统、医学图像系统等领域所构造和使用的模型越来越精细、越来越复杂。这些复杂的模型不但对计算机的存储容量、处理速度提出了很高的要求、而且成为实时绘制、网络传输的瓶颈。因此模型简化成为非常重要的研究课题。模型简化是指在保持原模型几何形状基本不变的前提下，采用适当的算法减少该模型的面片数、顶点数和边数。

在图形学应用中，有很多产生网格的途径，比如从点云、CSG模型、体数据等进行生成。随着计算机技术的不断发展，这些方法生成的网格越来越大，有些甚至超出了普通PC机内存的装载能力。它们中间比较著名的有斯坦福[1]和IBM实验室[2]对米开朗基罗的雕塑进行扫描与重建所得到的模型。这些模型能够提供非常精细的细节，但普通PC机内存无法装载和渲染，因此需要对这些模型进行简化。本文针对以上问题，提出了三种不同应用场景下的简化算法。

大规模网格分片简化是针对通过不同途径生成的超过了内存装载能力的网格，使用基于外存的技术进行简化的方法。大规模网格对简化算法本身提出了很大的挑战，因为常规的内存简化算法无法直接应用于大规模网格。为了解决这个问题，有不同的技术被提出，试图平衡大数据外存文件的访问效率和网格的简化质量。

大规模等值面的即时简化是针对三维模型数据生成的等值面过大、甚至超过了内存的装载能力、难以处理，而提出的生成一部分就进行简化的方法。它不需要生成全部等值面，因此避免了耗时的基于外存的等值面生成和out-of-core简化。

近年来，出现了很多有代表性的模型简化算法，其中Galand的基于二次误差度量的边收缩算法是目前最常采用且有效的算法。其基本思想是以顶点到相关三角形平面的距离的平方和为误差度量，通过重复的边收缩操作对模型进行简化。

1  算法分析与设计

1.1基本概念：

定义1  三角网格是由三位空间中的三角形通过边和顶点连接而成的分段线性曲面。三角网格M可由顶点集V={v1,v2...vm}和三角集合F={f1.f2...fn} 组成的二元组M=(V,F)来表示

定义2 对M种任一顶点vi，与顶点vi相关的三角形集合记作Planes(i)，与边(vi,vj)关联的三角形集合记作Planes(i,j)，所有与vi关联的边构成的集合Edge(i)。

1.2 基于二次误差度量的边收缩算法

基于二次误差度量的边收缩算法是通过不断选择模型中的一条边进行收缩，达到对模型的简化。每收缩一条非边界边，模型减少2个三角形、1个顶点、三条边；收缩一条边界边，模型减少1个三角形、1个顶点、俩条边。

1.2.1 误差度量

简化模型必须与原网格尽量相似，这取决于边收缩的顺序和边收缩后生成的新点的位置。如何选择合适的边进行收缩及如何生成新的顶点，有一个选择误差度量标准的问题。Garland算法以点到平面的距离为误差度量标准。

设对边(vi,vj)进行收缩，则与(vi,vj)边相关联的三角形集合Planes(i,j)构成了原模型上的一个区域，设边收缩后生成的新位置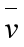为[x,y,z,1]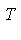，定义这次边收缩带来的新误差

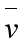△()为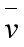到三角形集合Planes(i,j)中每个三角形所在面的距离的平方和，表示三角形集合Planes(i,j)中的每个三角形所在面的平面方程ax+by+cz+d=0，且有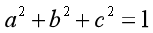。在根据点到平面ax+by+cz+d=0的距离公式为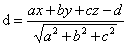以及等式运算 ,就有△(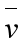)=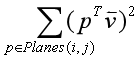其中：p=(a,b,c,d)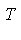该式可变换如下：

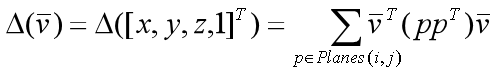
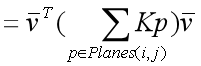
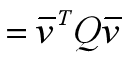
其中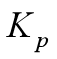：为4*4的对称矩阵，称为三角形的误差矩阵，它的定义如下

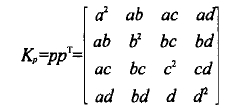
Q称为该次收缩的误差矩阵，定义如下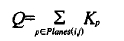

1.3 本小组关于Garland算法的一种实现。

为了简化算法实现的效率问题,使用本组关于Galand算法的一种实现:

1、取边收缩的误差矩阵Q为边的俩顶点收缩的误差矩阵Qi和Qj之和，即(Q=Qi+Qj)。

2、取新顶点位置为收缩边(i,j)中的一个，误差由公式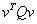计算得到，具体的选择由i收缩到j的所产生的误差和由j收缩到i所产生的误差值做比较得到的较小值决定。

3、实际边收缩带来的结果是 删除一个点，删除一条边，删除俩个与边关联的三角形，增加新边、三角形。

具体算法步骤如下：

步骤1  根据给定的模型数据，计算出所有顶点的顶点误差矩阵Qi：为各平面对应的a、b、c关联矩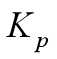阵的和:计算过程涉及求面的a、b、c(注意满足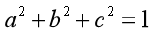)，即为面的单位法向量,单位法向量的求法可根据平面俩点的叉乘在单位化即可。

步骤2  设计一关于结构体的优先队列来简化堆的操作，存放i，j，及其收缩带来的误差，代表从i折叠到j的误差,并设计一哈希表用于判定是否新边。

步骤3  计算边折叠误差：根据步骤2，取边折叠从i到j和从j到i的教小者作为该边的误差入队并进入哈希散列。

步骤4  选择队列中的队头元素q出队(即代表从q.i折叠到q.j)。

步骤5  判断i，j同时相关的三角形的个数：如果个数大于1，那么删除与i，j同时关联的三角形，删除点i，进行边收缩(将剩余三角形中与i相关的三角形全部转移到与j相关),并往队列中增加由于折叠带来的新边(做与步骤3相同的操作)，否则转步骤4。

步骤6  如果边收缩达到给定的收缩哦边的个数，则结束收缩，否则转步骤4。

2、实验分析

2.1.1

原始牛模型 : 5804个三角片

2.1.2 简化后，三角片2804   简化时间2578ms

2.1.3进一步简化后，三角片1404  简化时间3235ms,

2.1.4更进一步简化，三角片704   简化时间3500ms

2.2..1

原始兔子模型 19859个三角片

2.2.2简化后 三角片 3859 简化时间  40375ms

2.2.2 进一步简化 三角片1859  简化时间41359ms

2.2.3 更进一步简化 三角片 1159  简化时间 41219ms

3、结束语

本次简化，在简化达到一定程度后，并不能确保保持具体信息，与Galand算法同样，存在着简化后的模型局部极大或极小的情况.

参考文献

[1] Levoy M, Pulli K, Curless B. The digital Michelangelo project: 3D scanning of large statues. Proceedings of the 27th annual conference on Computer graphics and interactive techniques, 2000: 131-144.

[2] Bernardini F, Rushmeier H, Martin I M. Building a digital model of Michelangelo's Florentine Pieta. Computer Graphics and Applications, IEEE, 2002, 22(1):59-67.

[3] Rossignac J R, Borrell P. Multi-resolution 3D approximations for rendering complex scenes. Geometric Modeling in Computer Graphics, 455–465. Springer, Berlin (1993).

[4] Low K-L, Tan T-S. Model simplification using vertex-clustering. Proceedings of the 1997 symposium on Interactive 3D graphics, 1997: 75-81.

[5] Luebke D, Erikson C. View-dependent simplification of arbitrary polygonal environments. Proceedings of the 24th annual conference on Computer graphics and interactive techniques, 1997: 199-208.

[6] Hinker P, Hansen C. Geometric optimization. Proceedings of the 4th conference on Visualization'93, 1993: 189-195.

[7] Kalvin A D, Taylor R H. Superfaces: Polygonal mesh simplification with bounded error. Computer Graphics and Applications, IEEE, 1996, 16(3):64-77.

[8] De Fioriani L, Magillo P, Puppo E. Building and traversing a surface at variable resolution. Visualization'97. Proceedings, 1997: 103-110.

[9] De Floriani L, Magillo P, Puppo E. Efficient implementation of multi-triangulations. Visualization'98. Proceedings, 1998: 43-50.

[10] Hamann B. A data reduction scheme for triangulated surfaces. Computer Aided Geometric Design, 1994, 11(2):197-214.