贪心搜索下的俄罗斯方块

1. 算法介绍

贪婪局部搜索算法每次从当前解的临近解空间中选择一个最优解作为当前解，直到达到一个局部最优解。该实   现很简单，其主要缺点是会陷入局部最优解，而不一定能搜索到全局最优解。

2. 项目问题介绍

2.1. 俄罗斯方块问题

2.1.1 原问题

由小方块组成的不同形状的板块陆续从屏幕上方落下来，玩家通过调整板块的位置和方向，使它们在屏幕底部拼出完整的一条或几条。这些完整的横条会随即消失，给新落下来的板块腾出空间，与此同时，玩家得到分数奖励。   没有被消除掉的方块不断堆积起来，一旦堆到屏幕顶端，玩家便告输，游戏结束，本游戏得分越高越好。

2.1.2 改编问题

在原问题的基础上我增加了俄罗斯方块的目标状态—指定目标状态需要达到的分数，达到时即为贪心搜索成功。如果未达到目标状态就违反了俄罗斯方块的规则，就认为贪心搜索失败。同时搜索成功或失败时，输出整个搜   索路径中随机产生的俄罗斯方块形状、方块放置的状态和其中心被放置的位置，这个作为本次贪心搜索的搜索路径。

2.2. 俄罗斯方块规则

2.2.1 游戏窗口

一个用于摆放小型正方形的平面虚拟场地，其标准大小：行宽为 10，列高为 20，以每个小正方形为单位。

2.2.2 游戏规则

一组由 4 个小型正方形组成的规则图形，英文称为 Tetromino，中文通称为方块。共有 7 种，分别以 S、Z、L、J、I、O、T 这 7 个字母的形状来命名。

I：一次最多消除四层J（左右）：最多消除三层，或消除二层 L：最多消除三层，或消除二层    O：消除一至二层S（左右）：最多二层，容易造成孔洞

Z （左右）：最多二层，容易造成孔洞

T：最多二层 主要规则如下：

（1）玩家可以做的操作有：以 90 度为单位旋转方块，以格子为单位左右移动方块，让方块加速落下。

（2）方块移到区域最下方或是着地到其他方块上无法移动时，就会固定在该处，而新的方块出现在区域上方开   始落下。

（3）随着玩的时间越来越长，方块下落的速度也越来越快，难度越来越高。

（4）当固定的方块堆到区域最上方而无法消除层数时，则游戏结束。

（5）当区域中某一列横向格子全部由方块填满，则该列会消失并成为玩家的得分。计分规则：如果一个方块消   除了 n 行，则本次消除得分为 n*(n-1)+1 分，即一次消除行数越多，得分越高。

（6）一般来说，游戏还会提示下一个要落下的方块，熟练的玩家会计算到下一个方块，评估要如何进行。

2.2.3 总结

通过设计者预先设置的随机发生器不断地输出单个方块到场地顶部，以一定的规则进行移动、旋转、下落和摆放，锁定并填充到场地中。每次摆放如果将场地的一行或多行完全填满，则组成这些行的所有小正方形将被消除， 并且以此来换取一定的积分或者其他形式的奖励。而未被消除的方块会一直累积，并对后来的方块摆放造成各种影响。

3. 项目问题分析

对于改编的俄罗斯方块问题，可以把每放一个方块的窗口界面状况和得分情况看做一个状态，只有当前的窗口   界面状况较好才能在未来获得较高的分数，状态转化的目的就是使得获得的分数可以达到目标状态的分数值，并且   状态转化的每一步都对未来状态有影响，同时只有保证自己能够存活下去才可能获取足够高的分数，因此综合考虑，我决定选择在保证界面状态较好的情况下，使得每一次获取的分数值尽可能大这样的贪心搜索算法，只有每一   个状态最优，才能较快地搜索到目标状态。

俄罗斯方块问题由于下落方块具有随机性，并且当前仅提供两个方块的信息，无法获得未来 2 步以上的方块信息，因此由于信息的局限性，本问题无法求出全局最优解，但通过构造代价评估函数，可以确保每步可以选择最   优的状态，进而在整体上能够实现较好的性能。但当最终将要抵达目标状态时，要判断此时每一次的得分情况，放   置分数超过目标状态。

3.1. 问题的表示

对于问题的表示有以下的的元组表示法

p = (I, G, O, C) (1)

而对于本问题中 I 为游戏的开始阶段，即 10 列 20 行的空白游戏窗口，0 分的初始分数，G 为目标状态，即达到了预定的分数和目标窗口（主要以是否达到目标分数来评判是否达到目标状态）。而对于 O 的选择则包括游戏规则和贪心搜索方法，C : O × S → R+

3.1.1 O 中的游戏规则

游戏规则如 2.2 所诉，这是贪心搜索算法索要遵循的规则。

3.1.2 O 中贪心搜索

对于俄罗斯方块每次产生一个方块，遍历整个游戏窗口，找到方块可以放置的所有位置，放置过方块后改变的   游戏窗口均对应了一个状态，相当于在图中找到了当前结点的相邻点，然后通过构造出的代价评估函数，比较这些相邻状态中，哪个状态的函数值最大（这个构造出的代价函数函数值越大，表示状态越优），当有多个状态的函数值相等时，则比较其最优先函数值，值小的优先被选。以下算法将以构造代价评估函数为中心进行叙述。

3.2. 基本共识

3.2.1 经验共识

构造问题的评估函数，要以一定的基本共识作为基础，该共识是人们的经验总结和分析的结果。

• 共识一：尽可能地消除行，不要累积高度。

• 共识二：一次尽可能地多消除行，以便利用加分规则，多加分。

• 共识三：出现板块复杂的局面，要尽量避免“气泡”的数量，让空的格子较少。  总结以上共识可以得出以下五个参数 [2]。

3.2.2 参数设置

• 当一块板块摆放之后，与这个板块接触的小方块的数量是一个需要考虑的参数。很显然，与值接触的小方块   越多，说明这个板块摆放再改位置后产生的“空洞”的数量越少，如果一个“棋盘”局面中空的小方块或者“空洞”数量少则说明这个局面对玩家有利。

• 当一个板块摆放在某个位置之后，这个板块的最高点的高度是一个需要考虑的参数。这个高度会影响整体的   高度，当有两个位置可选择摆放位置时，应该优先放置再板块最高点的高度比较低的位置上。

• 当一个板块摆放在某个位置之后能消除的行数是一个重要参数。毫无疑问，消除的行越多越好。

• 游戏区域中已经被下落板块填充的区域中空的小方格的数量也是评价游戏局面的一个重要参数。很显然，每   一行中空的小方格数量越多，局面对玩家越不利。

• 游戏区域中已经下落板块填充的区域中“空洞”的数量也是一个重要参数。如果一个空的小方格上方被其他板块的小方格挡住，则这个小方格就形成了“空洞”，“空洞”是俄罗斯方块游戏中最难处理的情况，必须等上层的小方块都消除之后才有可能填充“空洞”，很显然，这是一个能恶化局面的参数。

所以摆放策略是板块放置的位置越靠下越好，方块之间越紧密越好，自身对消除行的方块贡献数量越多越好。因此，要在追求消除行数最大化的同时，又要保证产生的“气泡”最少。

通过阅读论文 [1]得知，以上策略可以通过六个属性来抽象。

3.2.3 属性抽象

• landingHeight: 指当前板块放置之后，板块重心距离游戏区域底部的距离。（也就是小方块的海拔高度）

• erodedPieceCellsMetric: 这是消除参数的体现，他代表的是消除的行数与当前摆放的板块中被消除的小方块的格数的成绩。

• boardRowTransitions: 对于每一行小方格，从左往右看，从无小方格到有小方格是一种“变换”，从有小方格到无小方格也是一种“变换”，这个属性是各行中“变换”之和

• boardColTransitions: 这是每一列的变换次数之和

• boardBuriedHoles: 各列中的“空洞的小方格数之和”

• boardWells: 各列中“井”的深度的连加和（“井”的定义是，两边（包括边界）都有方块填充的空列）

3.3. 构造代价评估函数

value = − landingHeight + erodedP ieceCellsM etric − boardRowT ransitions−

boardColT ransitions − (4xboardBuriedHoles) − boardW ells

通过论文 [1]得知，经过遗传算法实验。根据各指标的权重的经验值修改评估函数为

value = − 45×landingHeight + 34×erodedP ieceCellsM etric − 32×boardRowT ransitions

− 93×boardColT ransitions − (79×boardBuriedHoles) − 34×boardW ells

该评估函数越小越好。

当多个状态 value 值相等时，定义其优先函数若板块摆放在游戏的左侧（1-5 列）

(2)

(3)

priority = 100 × 板块需要水平移动移动的次数 + 板块需要选择的次数 + 10 (4)

若板块摆放在游戏的右侧（6-10 列）

priority = 100 × 板块需要水平移动移动的次数 + 板块需要选择的次数 (5)

该优先函数越小越好。因为本游戏是 10 列，且方块初始下降在第 5 列，所以当方块摆在游戏的左侧时，要加上 10。

3.4. 中止条件

由于每次消除行数最多消除 4 行，即最多得 13 分。因此需要在目前得分与目标得分相差 13 分之内添加限制条件，防止得分超过目标状态，使得搜索失败。我的解决办法是超前计算出每个位置放置后的得分，如果得分超过   目标状态与当前状态之间的差值，则舍弃此位置，在满足条件的位置处选择评估值最高的位置。一旦达到目标状态   则立即停止程序并打印出搜索路径。

4. 项目实施

4.1. 编程环境

pycharm2017.2.3 + python3.7.0

4.2. 程序类图

本项目的程序类图 (包括类的作用和关系）如下：

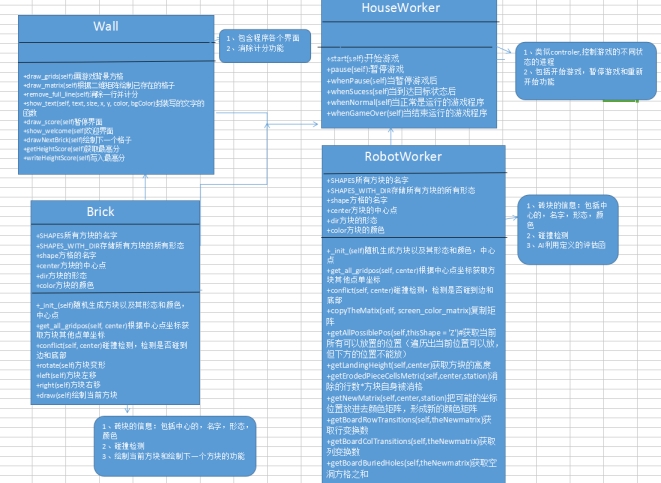
图 1. 程序类图

其中矩形代表一个类，圆角图形代表对类作用的解释。

4.3. 程序运行界面设置

程序界面分为两个部分，左边是游戏界面，右边为信息界面。游戏界面是俄罗斯方块的图形游戏界面，而信息界面则是包括得分栏（目前得分、当前等级、目标分数），信息框（一些操作时的信息提示：成功提示、失败提示、开始提示等），操作栏（各个操作的切换快捷键设置）和作者信息。具体界面见 4.4 程序运行效果。

4.4. 程序运行效果

4.4.1 运行效果图

以下为项目运行的界面，包括开始界面、两个运行时界面、成功界面和暂停界面。

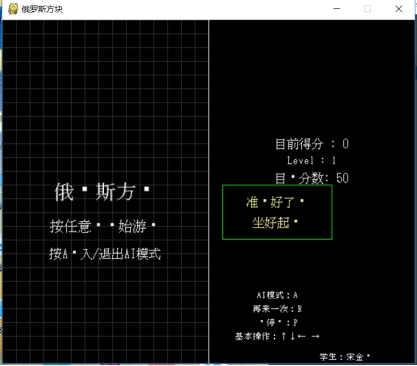
图 2. 游戏开始界面

图 3. 游戏进行界面 1

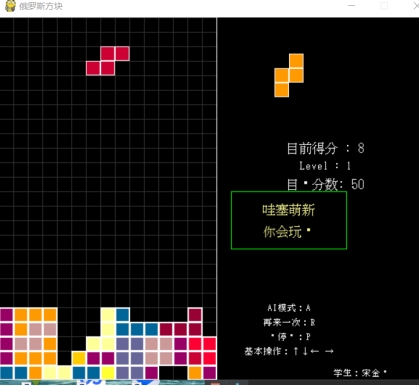
图 4. 游戏进行界面 2

图 5. 成功界面

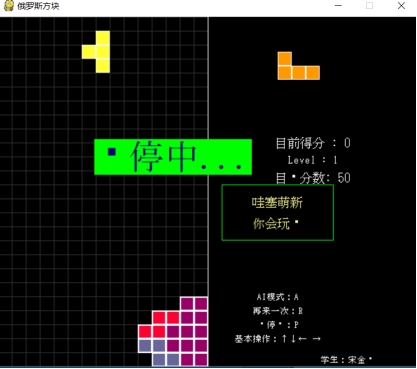
图 6. 暂停界面

4.4.2 运行结果

项目的运行效果包括找到目标状态后的图形效果和储存的搜索路径（每个路径点包括方块放置的中心点，放置   的方向，方块的形状）对于目标状态 50 分以下为运行结果图

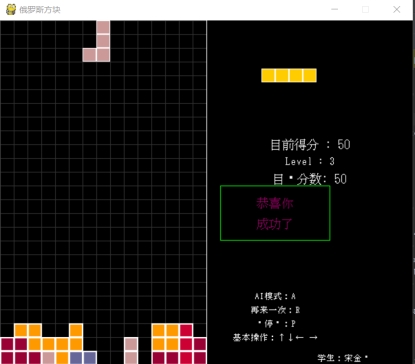
图 7. 成功界面

以下为保存的路径：对于 [’center’: [22, 14], ’station’: 2, ’L’] 来说，’center’: [22, 14] 为放置方块的中心点，

’station’: 2 为其方块放置的方向，’L’ 为其形状。这个路径存为一个列表：

[[’center’: [22, 14], ’station’: 2, ’L’], [’center’: [23, 12], ’station’: 1, ’T’], [’center’: [21, 14], ’station’: 3, ’L’],

[’center’:  [22, 11], ’station’:  1, ’I’], [’center’:  [19, 14], ’station’:  1, ’Z’], [’center’:  [17, 13], ’station’: 1, ’T’], [’center’:

[15, 13], ’station’: 0, ’S’], [’center’: [20, 12], ’station’: 0, ’J’], [’center’: [17, 11], ’station’: 2, ’J’], [’center’: [22, 10],

’station’:  2, ’L’], [’center’:  [19, 10], ’station’:  1, ’I’], [’center’:  [16, 10], ’station’:  1, ’L’], [’center’:  [23, 7], ’station’:

1, ’L’], [’center’:  [21, 8], ’station’:  1, ’T’], [’center’:  [19, 9], ’station’:  3, ’T’], [’center’:  [23, 5], ’station’:  0, ’O’],

[’center’:  [23, 3], ’station’:  0, ’S’], [’center’:  [21, 4], ’station’:  0, ’Z’], [’center’:  [21, 5], ’station’:  0, ’S’],  [’center’:

[19, 3], ’station’: 0, ’O’], [’center’: [18, 4], ’station’: 0, ’S’], [’center’: [20, 6], ’station’: 0, ’S’], [’center’: [22, 2],

’station’: 1, ’I’], [’center’: [18, 8], ’station’: 1, ’Z’], [’center’: [18, 2], ’station’: 2, ’J’], [’center’: [15, 9], ’station’:

2, ’J’], [’center’:  [17, 6], ’station’:  2, ’T’], [’center’:  [15, 12], ’station’:  0, ’J’], [’center’:  [16, 6], ’station’:  0, ’I’],

[’center’:  [17, 2], ’station’:  0, ’L’], [’center’:  [13, 14], ’station’:  3, ’T’], [’center’:  [15, 4], ’station’:  1, ’S’], [’center’:

[14, 2], ’station’:  0, ’S’], [’center’:  [15, 8], ’station’:  3, ’L’], [’center’:  [14, 5], ’station’:  0, ’I’], [’center’:  [13, 4],

’station’: 0, ’I’], [’center’: [22, 1], ’station’: 1, ’I’], [’center’: [14, 11], ’station’: 3, ’L’], [’center’: [12, 10], ’station’: 1,

’S’], [’center’: [20, 0], ’station’: 2, ’J’], [’center’: [14, 4], ’station’: 0, ’I’], [’center’: [13, 4], ’station’: 0, ’I’], [’center’:

[21, 0], ’station’: 0, ’L’], [’center’: [15, 7], ’station’: 0, ’O’], [’center’: [14, 12], ’station’: 0, ’O’], [’center’: [19, 1],

’station’: 3, ’T’], [’center’: [18, 0], ’station’: 1, ’I’], [’center’: [18, 1], ’station’: 2, ’J’], [’center’: [19, 8], ’station’:

0, ’S’], [’center’: [19, 10], ’station’: 0, ’Z’], [’center’: [19, 7], ’station’: 3, ’J’], [’center’: [18, 11], ’station’: 0, ’O’],

[’center’:  [18, 3], ’station’:  0, ’O’], [’center’:  [19, 13], ’station’:  0, ’S’], [’center’:  [18, 8], ’station’:  0, ’I’], [’center’:

[17, 14], ’station’: 3, ’J’], [’center’: [20, 1], ’station’: 2, ’T’], [’center’: [19, 10], ’station’: 0, ’T’], [’center’: [21, 1],