主成分分析

问题来源：

真实的样本往往维数很高，但是复杂的唯独下可能信息量不高，一些维度之间的相关性很高，对这些数据直接进行监督或非监督学习往往效率较低。在决策树一章里，给定了若干维特征，我们用这若干维特征去剪枝构造决策树时会选取一部分特征，剔除一部分特征，选择特征时按照信息增益（互信息）多少来选择，因此剪枝地构造决策树是一种降低维度的手段。 下面探讨一种称作主成分分析（PCA）的方法来解决部分上述问题。PCA的思想是将n维特征映射到k维上（k<n），这k维是全新的正交特征。这k维特征称为主元，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n-k维特征。

实验原理：

刘老师上课时从最大方差的角度推出了pca算法。

我们认为，经过聚类之后的最好的k维特征是将n维样本点转换为k维后，每一维上的样本方差都很大。

比如下图有5个样本点：

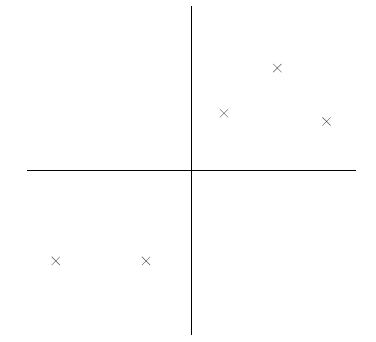
下面将样本投影到某一维上，这里用一条过原点的直线表示

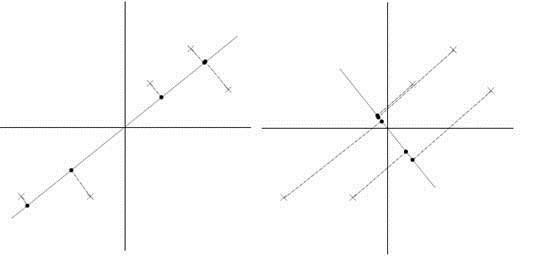
假设我们选择两条不同的直线做投影，问题的关键在于那么左右两条中哪个好。根据我们之前的方差最大化理论，左边的好，因为投影后的样本点之间方差最大。投影之后保留的信息量更大。

设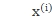为样本的对应的向量表示，u为要投影方向的单位向量。

由于这些样本点（样例）的每一维特征均值都为0(这一点在样本处理时很容易做到，也是下文中样本处理的第一步)，因此投影到u上的样本点（只有一个到原点的距离值）的均值仍然是0。

所以投影后的方差为

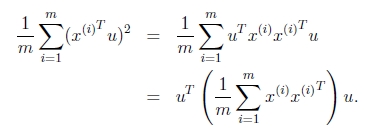
Σ=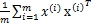，即为协方差矩阵，

令λ=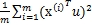（优化目标）

有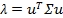             （1）

又因为μ为单位向量，所以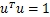

对（1）式左乘μ，得到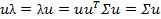

所以λ为原协方差矩阵的特征值，μ为相对应的特征向量。

最佳的投影直线是特征值最大时对应的特征向量，其次是第二大对应的特征向量，依次类推。

实验步骤：

样本的来源，随机生成一个矩阵，行代表了样例，列代表特征，在这里我随机生成一个10行8列的样本矩阵，即有10个样本，每个样本8个特征。

第一步：分别求每个特征的平均值，然后对于所有的样例的每一维特征，都减去对应的均值。pca算法推导的条件所需。

第二步，对特征做方差归一化，求每个特征的标准差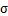，然后对每个样例在该特征下的数据除以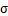。每一维特征方差可能差别较大。

第三步：求协方差矩阵，协方差矩阵对角线上的数为每维特征的方差，非对角线上的数为协方差。协方差大于0，说明两个特征之间正相关，协方差小于0，说明特征之间负相关。

第四步，求协方差矩阵的特征值和特征向量。

第五步，将特征值按照从小到大的顺序排序，选择最大的K个，然后将对应的K个特征向量（列向量）最为特征向量矩阵。在本实验中，我们选K=5.

第六步，将样本点投影到选取的特征向量上。样例数为10，特征数为8，减去均值以及用标准差做归一化后的样本矩阵为stded (10*8)，协方差矩阵是8*8，选取的k个特征向量组成的矩阵为seleEigVects (8,5) 。那么投影后的数据lowDDataMat（10，5）为

lowDDataMat=stded*seleEigVects

实验结果分析：

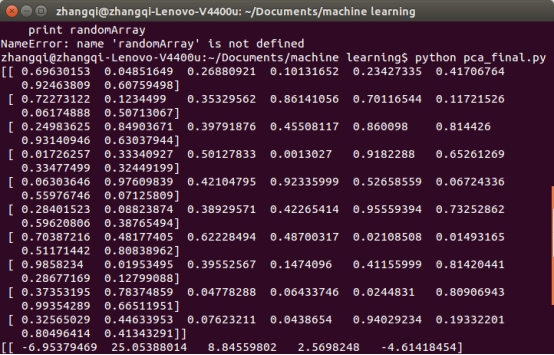
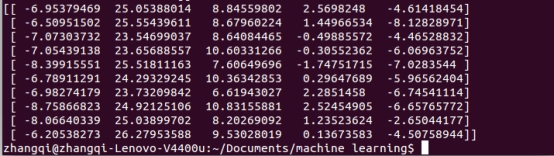
得到的结果即是这10个样本（每个样本的维数为8），每个样本的维数降到5以后的样本矩阵。将这10个样本投影到5维空间（基即为特征值，在该维度的方差即为对应的特征值）。

降维的本质并不是直接去掉一些维度，而是用低维度的基来表示高维度的数据。如果原来的样本在这些维度的信息量很大，则降维并没有损失大量的信息。

而得到的降维后的样本矩阵对应的是每个样本在投影向量上的权重。

重建（后来老师提出的一个概念），相当于pca的一个逆过程，将降维后的数据重新映射到高纬度，并加上一个平移。（可能是因为在降维过程的第一步减去了一个均值，使所有维度的均值为0了）

附录：实现代码

from numpy import *

#coding: utf-8

def pca(dataMat, K=5):

meanVals = mean_value(dataMat)

meanRemoved = dataMat - meanVals

stded = meanRemoved / std(dataMat,axis=0)

covMat = cov(stded, axis=0)

eigVals, eigVects = linalg.eig(mat(covMat))

eigValInd = argsort(eigVals)

eigValInd = eigValInd[-K:]

seleEigVects = eigVects[:, eigValInd]

lowDDataMat = stded * seleEigVects

return lowDDataMat

def mean_value(MAT):

mean_va=random.random(size=(1,8))

for j in range(MAT.shape[1]):

sum0=0

for i in range(MAT.shape[0]):

sum0=sum0+MAT[i][j]

mean_va[0,j]=sum0

return mean_va

randArray = random.random(size=(10,8))

a=pca(randArray)

reconMat = (a * seleEigVects.T) * std(dataMat) + meanVals  #重建

print a