摘 要
实验一：非线性方程求根
------二分法+牛顿法+牛顿下山法+弦截法
实验二：线性方程组的直接解法
------改进的Cholesky方法
实验三：线性方程组的迭代解法
------雅可比+SOR+共轭梯度法
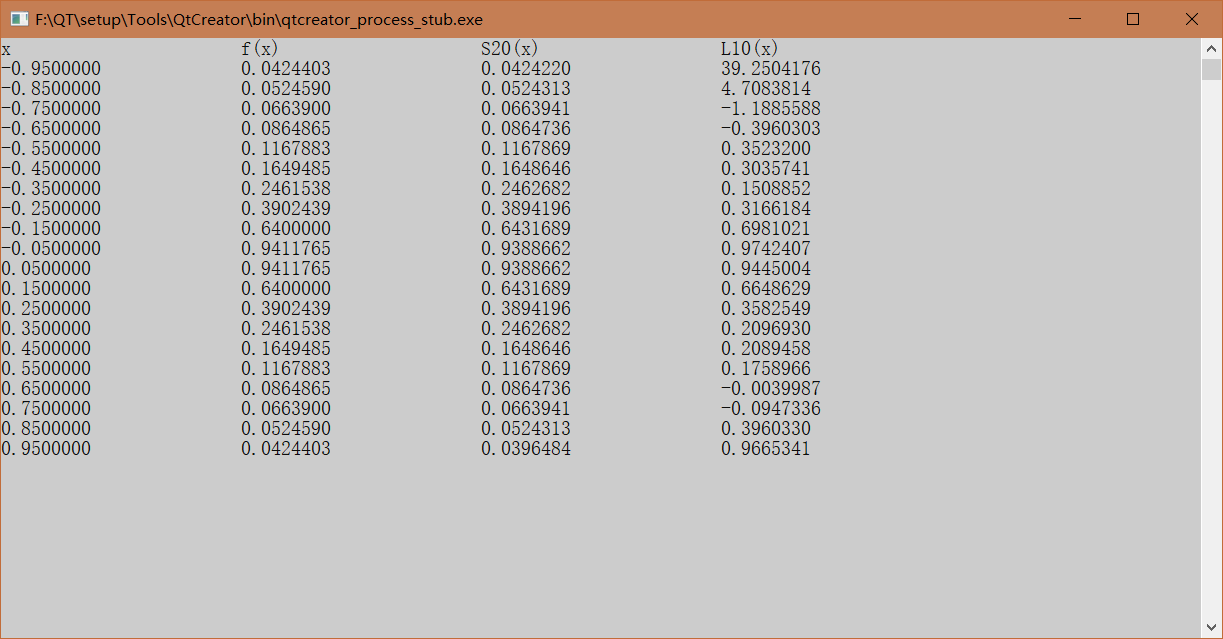
实验四：函数插值
------三次样条插值+拉格朗日插值法
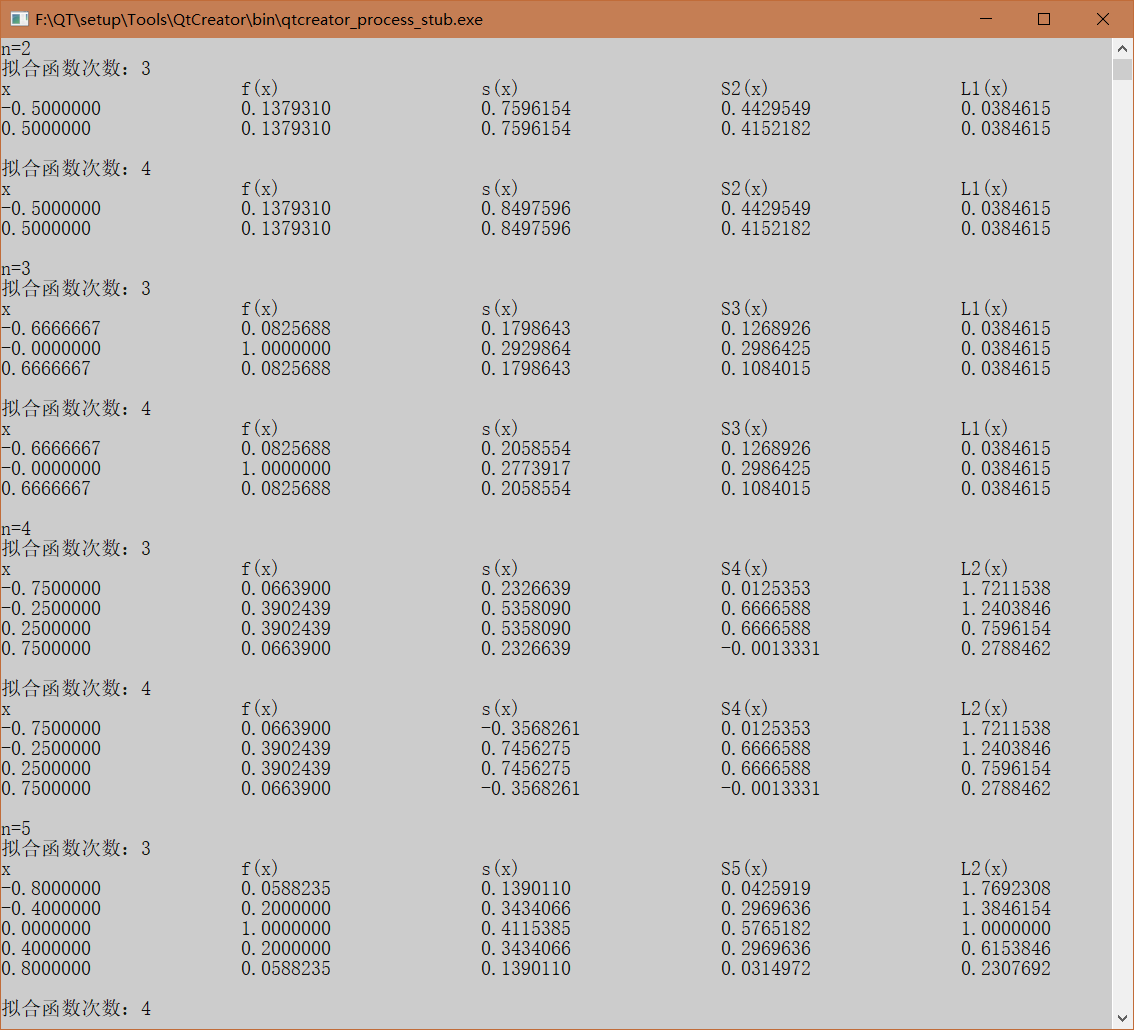
实验五：最小二乘数拟合
------最小二乘法+共轭梯度法+三次样条插值+拉格朗日插值法
实验六：数值积分
------龙格公式
关键词：二分法、牛顿法、牛顿下山法、共轭梯度法、改进的Cholesky方法、雅可比、SOR、共轭梯度法、三次样条插值、拉格朗日插值、龙格公式
目 录
实验一、非线性方程求根
一、实验内容：
二、算法基本思想及复杂度分析：
三、源程序及注释：
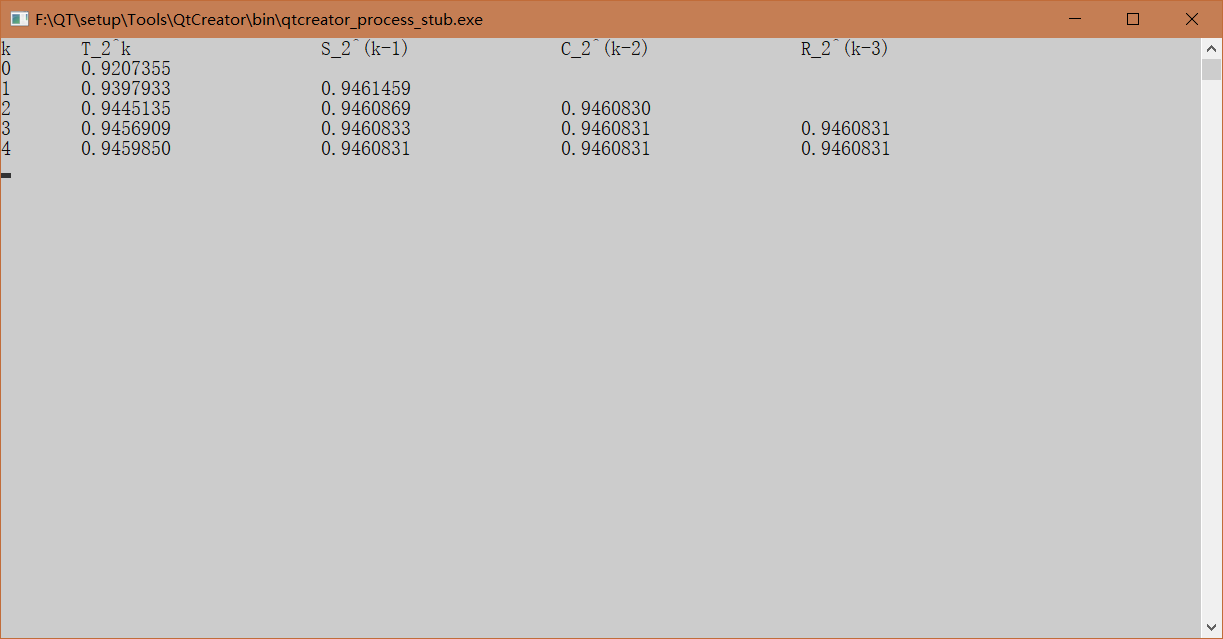
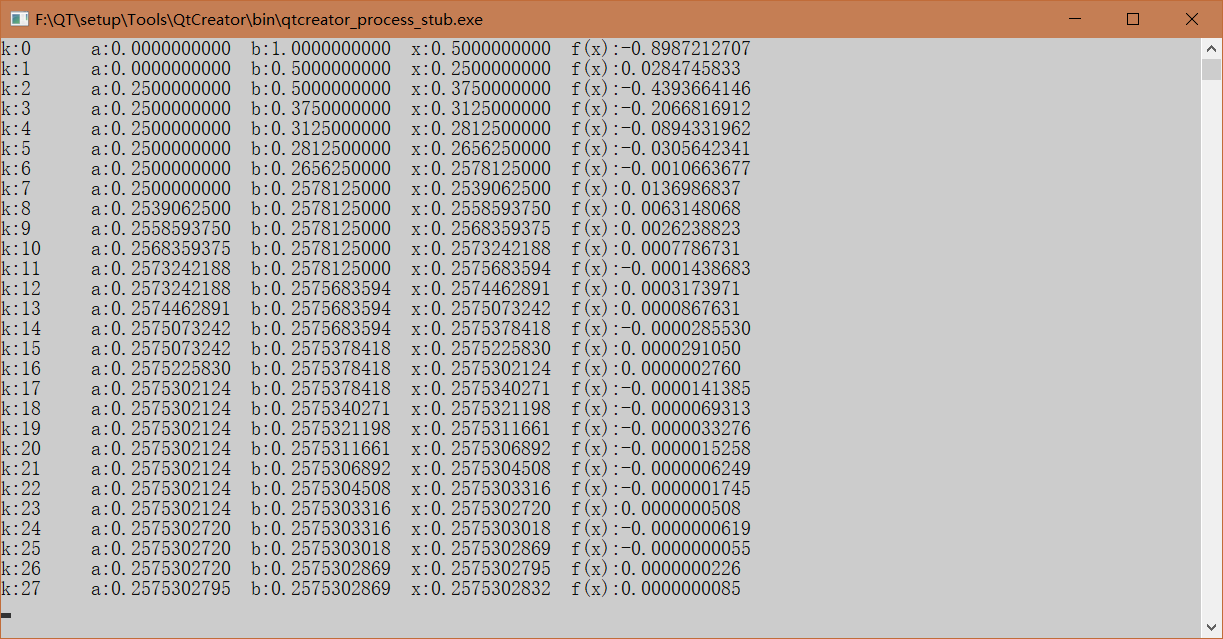
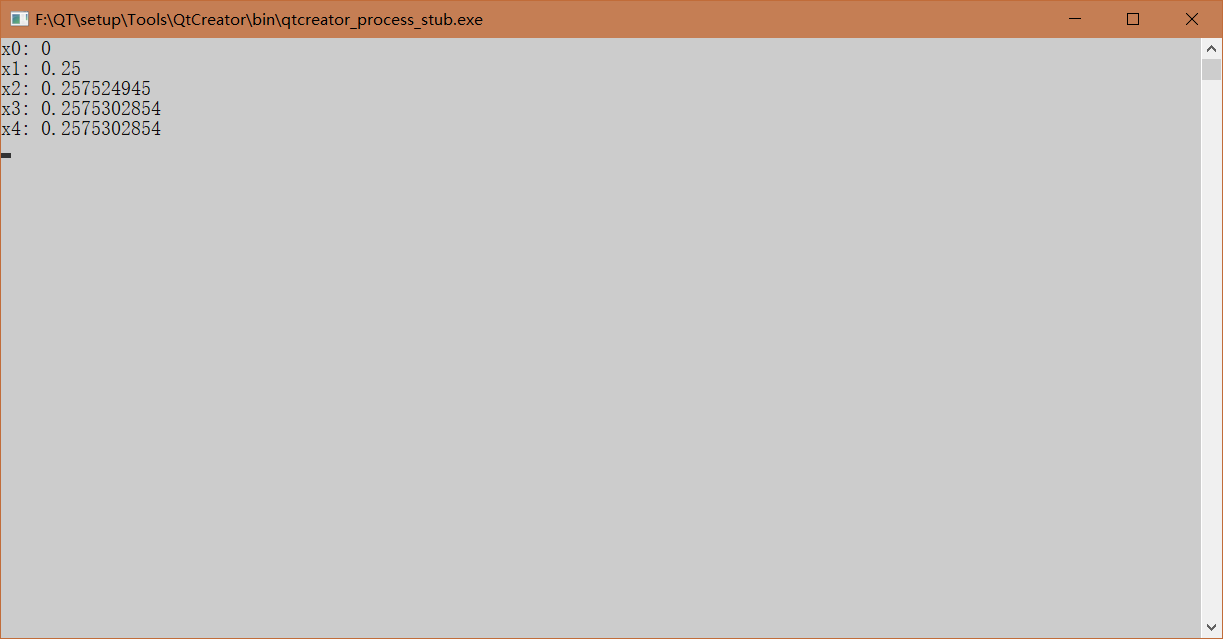
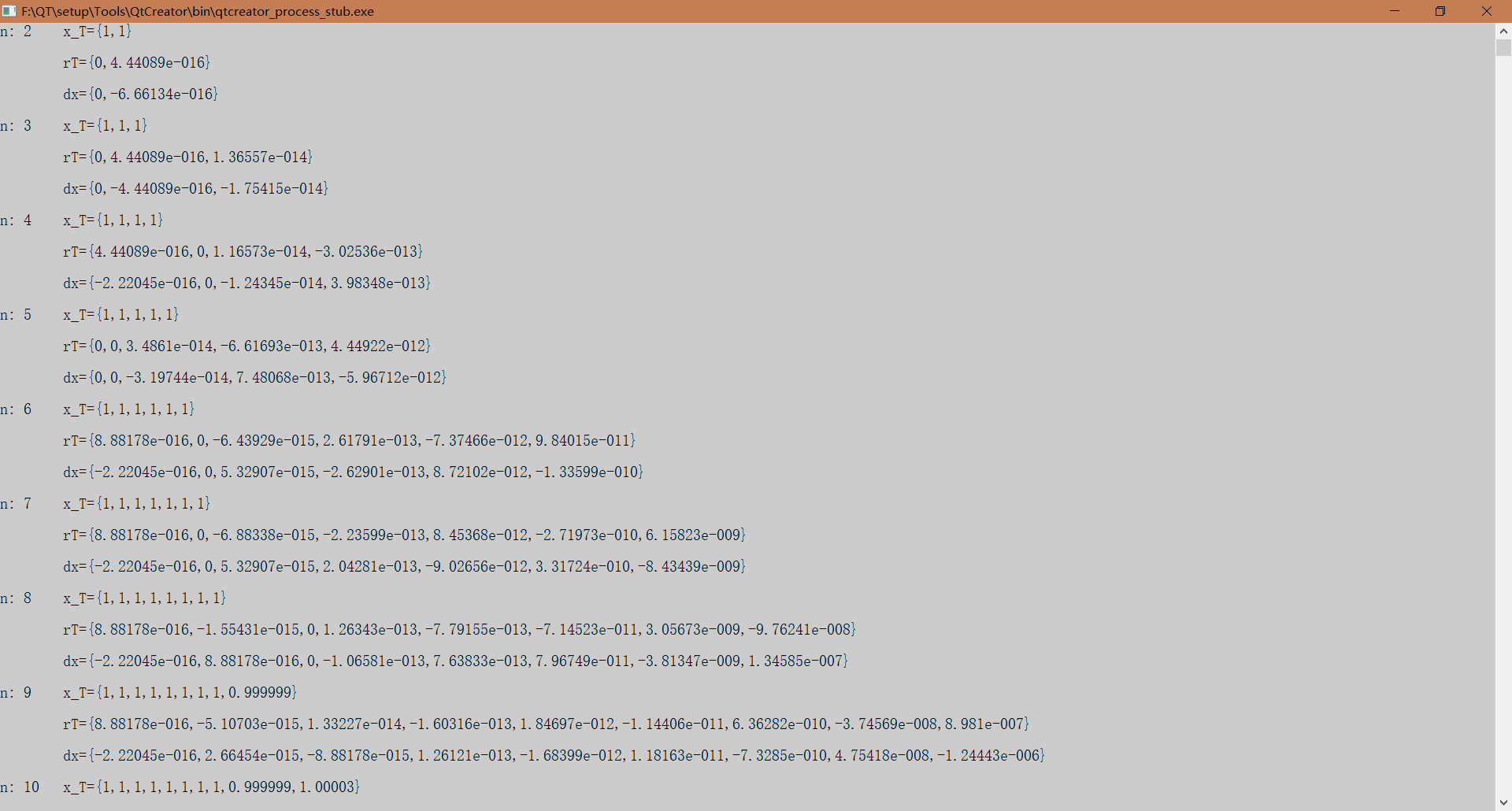
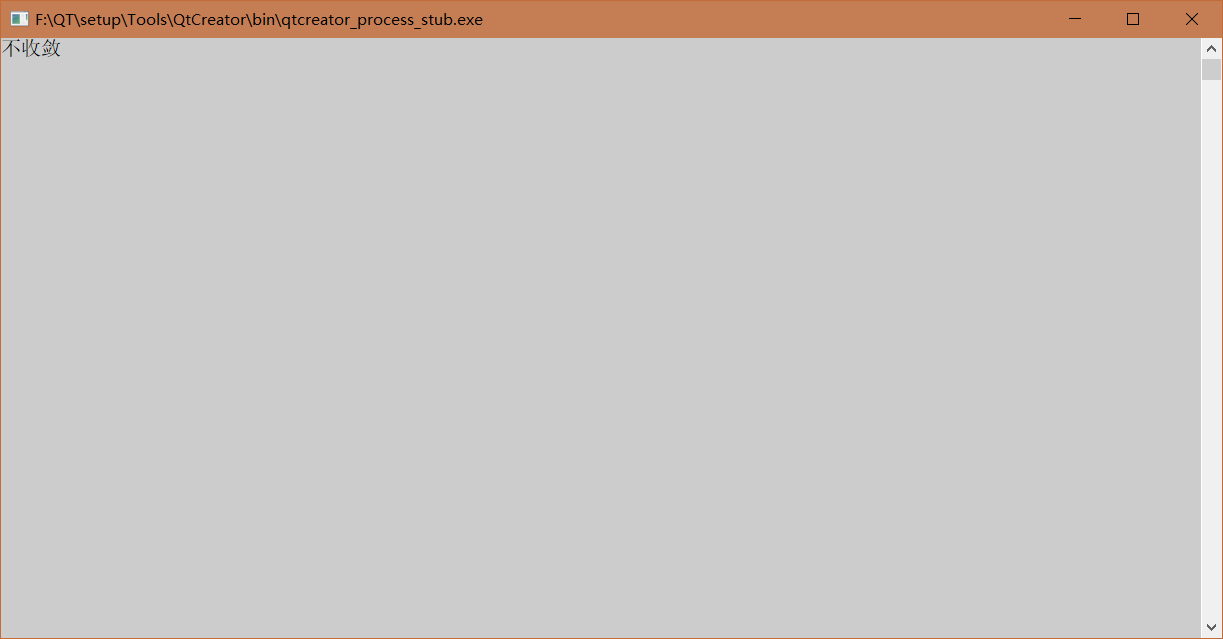
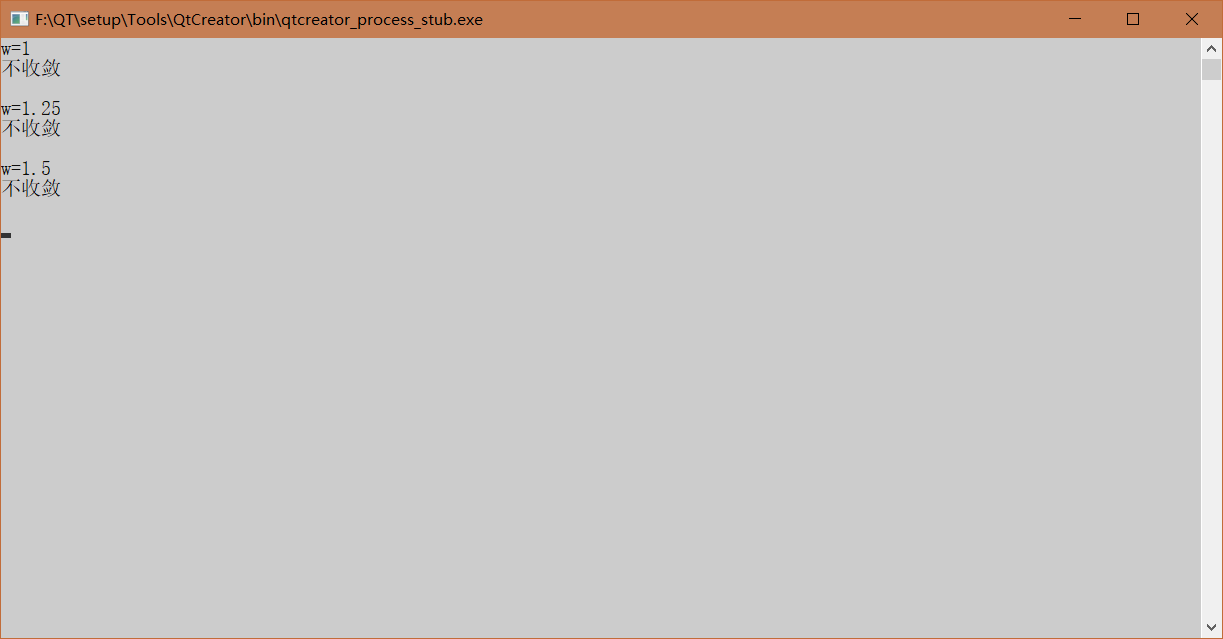
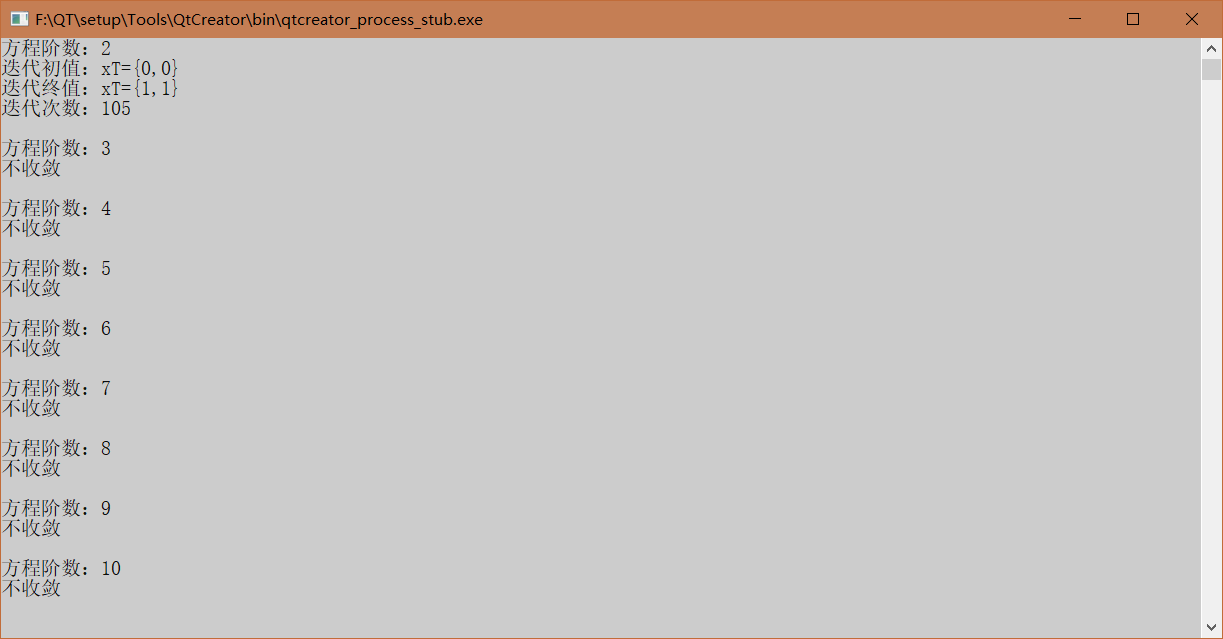
四、运行输出结果：
五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训：
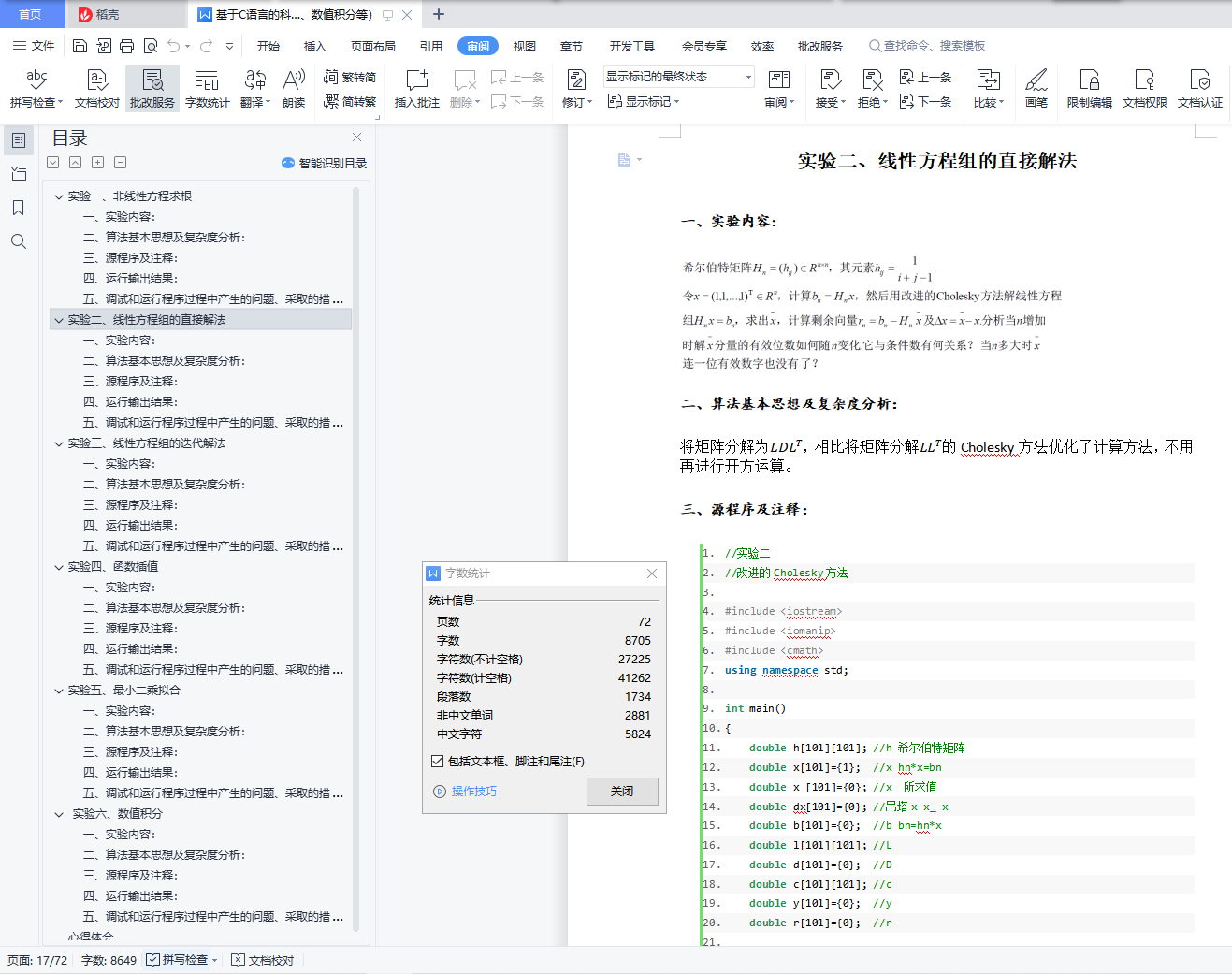
实验二、线性方程组的直接解法
一、实验内容：
二、算法基本思想及复杂度分析：
三、源程序及注释：
四、运行输出结果：
五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训：
实验三、线性方程组的迭代解法
一、实验内容：
二、算法基本思想及复杂度分析：
三、源程序及注释：
四、运行输出结果：
五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训：
实验四、函数插值
一、实验内容：
二、算法基本思想及复杂度分析：
三、源程序及注释：
四、运行输出结果：
五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训：
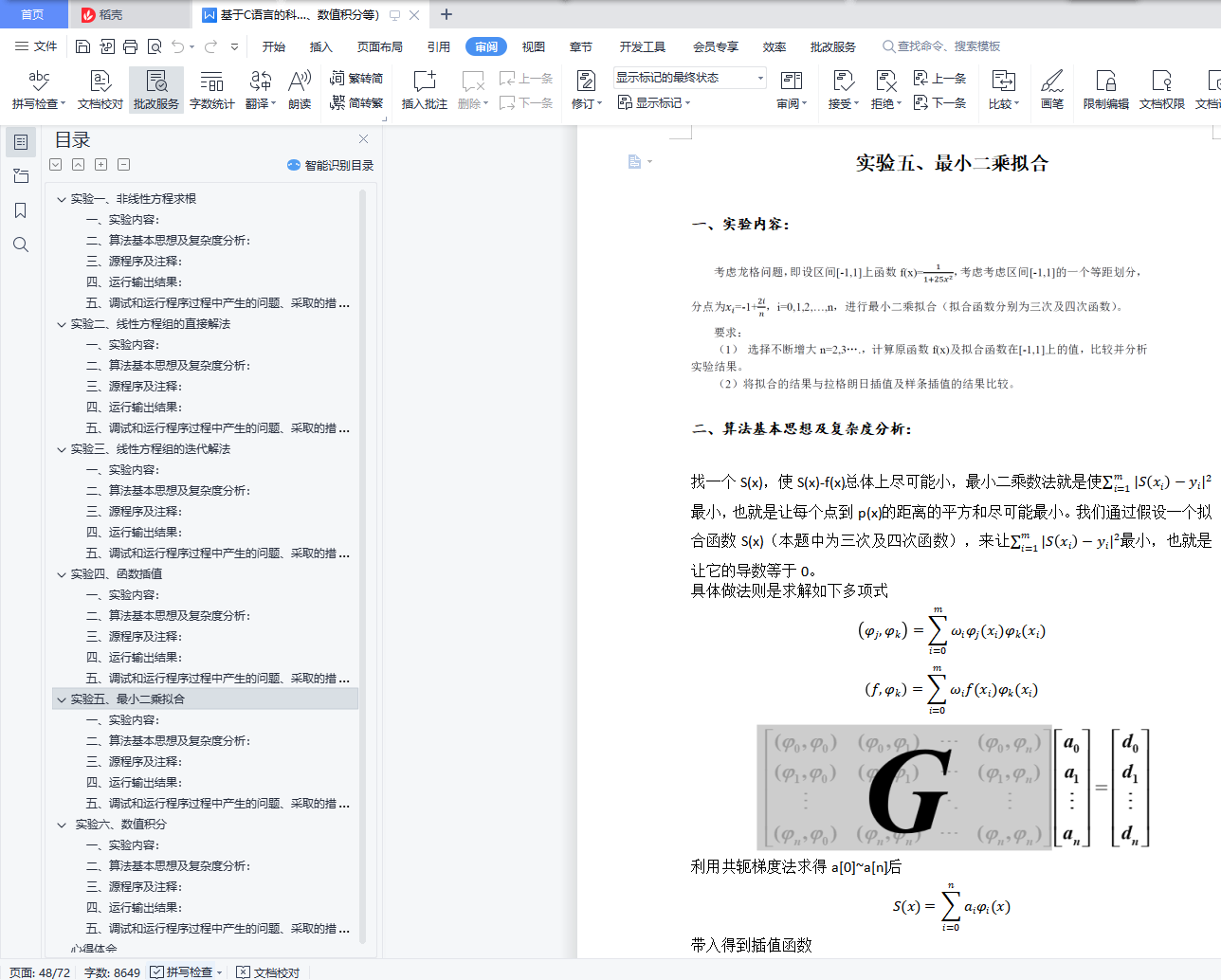
实验五、最小二乘拟合
一、实验内容：
二、算法基本思想及复杂度分析：
三、源程序及注释：
四、运行输出结果：
五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训：
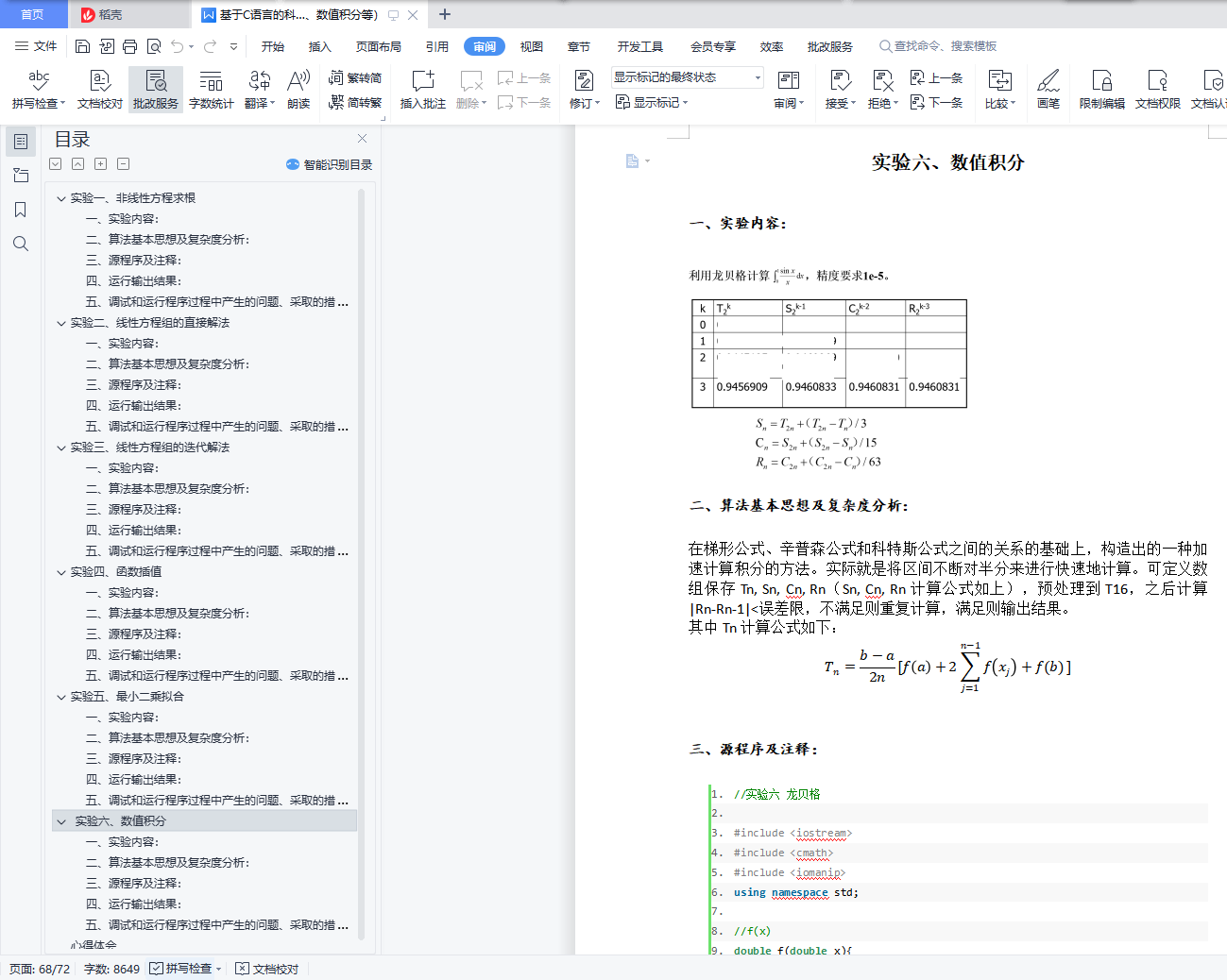
实验六、数值积分
一、实验内容：
二、算法基本思想及复杂度分析：
三、源程序及注释：
四、运行输出结果：
五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训：
心得体会
实验一、非线性方程求根
一、实验内容：
二、算法基本思想及复杂度分析：
（一）二分法
将有根区间对分，并找出根所在的小区间，然后再对该小区间对分，依次类推，直到有根区间的长度足够小为止。
（二）牛顿法
牛顿法是一种线性化方法，其基本思想是将非线性方程f(x)=0逐步归结为某种线性方程来求解。
（三）牛顿下山法
要求每一步迭代满足下降条件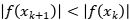
（保证全局有效）。也就是由于牛顿法的复杂度依赖于x0的选取，所以在牛顿法中加入了下山因子，且逐次减半。
（四）弦截法
当f(x)比较复杂的时候，f’(x)会比较难算，该方法就是用差商来取代牛顿法中的
f’(x)。
三、源程序及注释：
（一）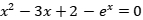
1. 二分法
1. //实验一（一）二分法
2. //f(x)=x^2-3x+2-e^x
3. //f(0)=1>0
4. //f(1)=-e<0
5. //由此 有根区间(a,b)确定为(0,1)
6.
7. #include <iostream>
8. #include <iomanip>
9. #include <cmath>
10. using namespace std;
11.
12. //f(x)=x^2-3x+2-e^x
13. double f(double x){
14. return x*x-3*x+2-exp(x);
15. }
16.
17. int main(){
18. double a=0; //(a,b)赋初值为(0,1)
19. double b=1;
20. double x=0.5; //x=(a+b)/2
21. double xt=0; //xt用来存储上一个x
22. int k=0; //k用来计数
23. while(fabs(f(x)-f(xt))>=1e-8){ //设置精度
24. cout<<"k:"<<k<<"\t"<<fixed<<setprecision(10)
25. <<" a:"<<a<<"\t b:"<<b<<"\t x:"<<x<<"\t f(x):"<<f(x)
26. <<endl;
27. xt=x;
28. if(f(x)<0){
29. b=x;
30. x=(a+x)/2;
31. }
32. else if(f(x)>0){
33. a=x;
34. x=(b+x)/2;
35. }
36. k++;
37. }
38. return 0;
39. }
