《算法设计与分析-大作业》实验报告
目录
《算法设计与分析-大作业》实验报告
一、实验内容:
二、所用算法的基本思想及复杂度分析:
三、源程序及注释:
四、运行输出结果:
五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训:
六、对授课的建议(如助教是大四的同学较好,还是大三的同级ACM同学较好;及其他)
一、实验内容:
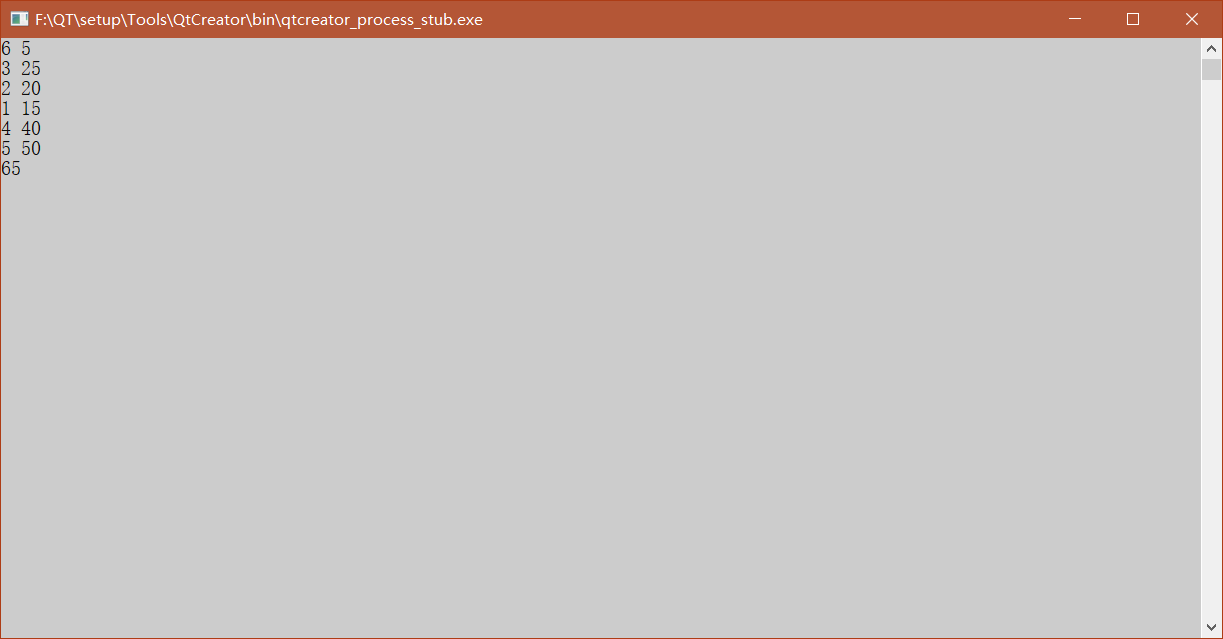
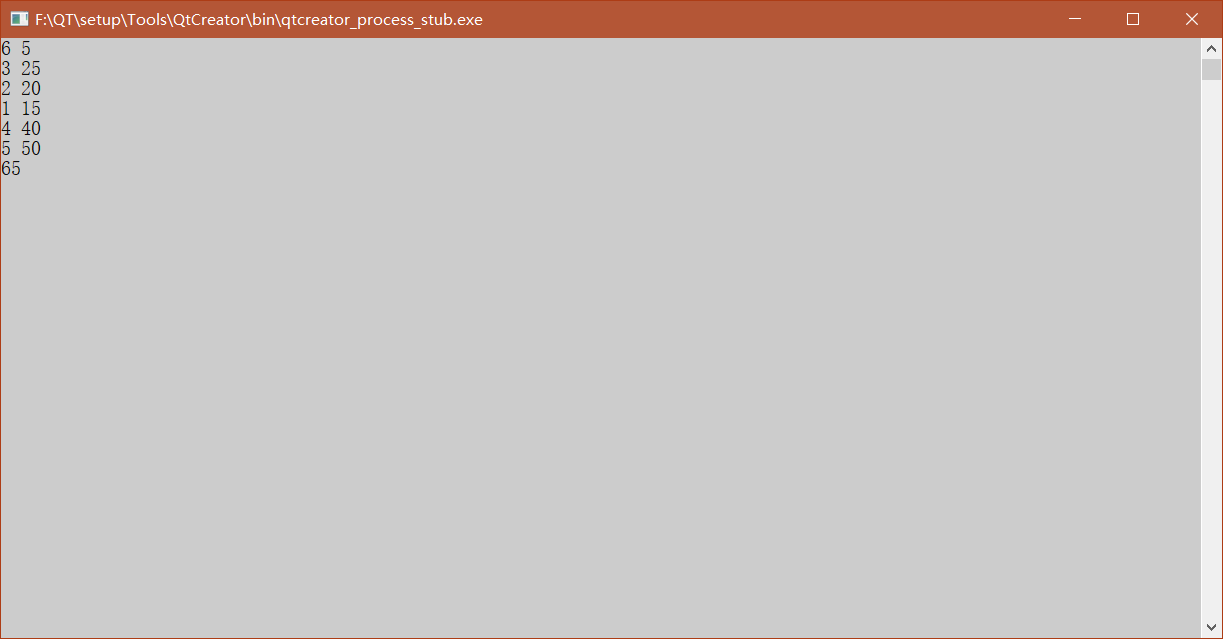
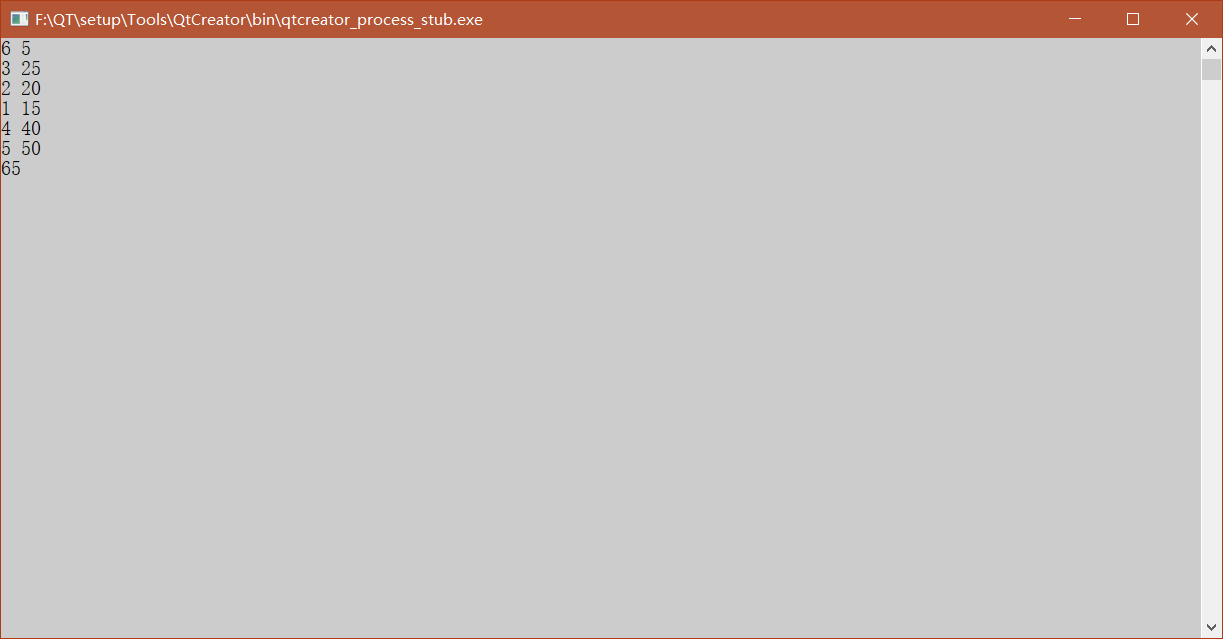
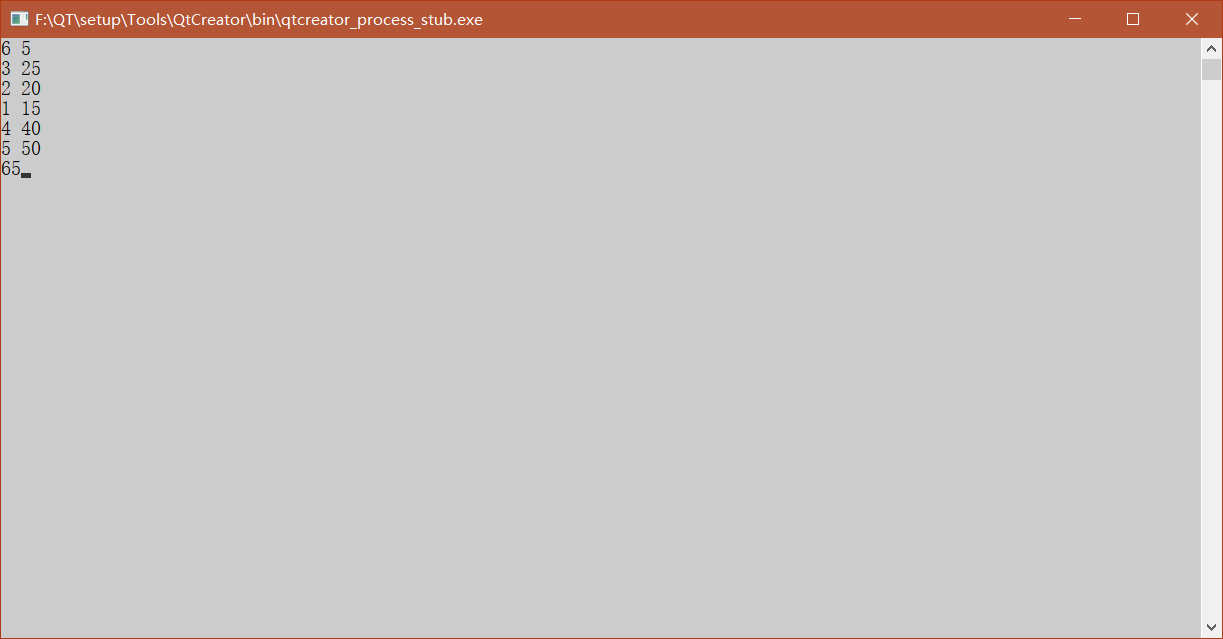
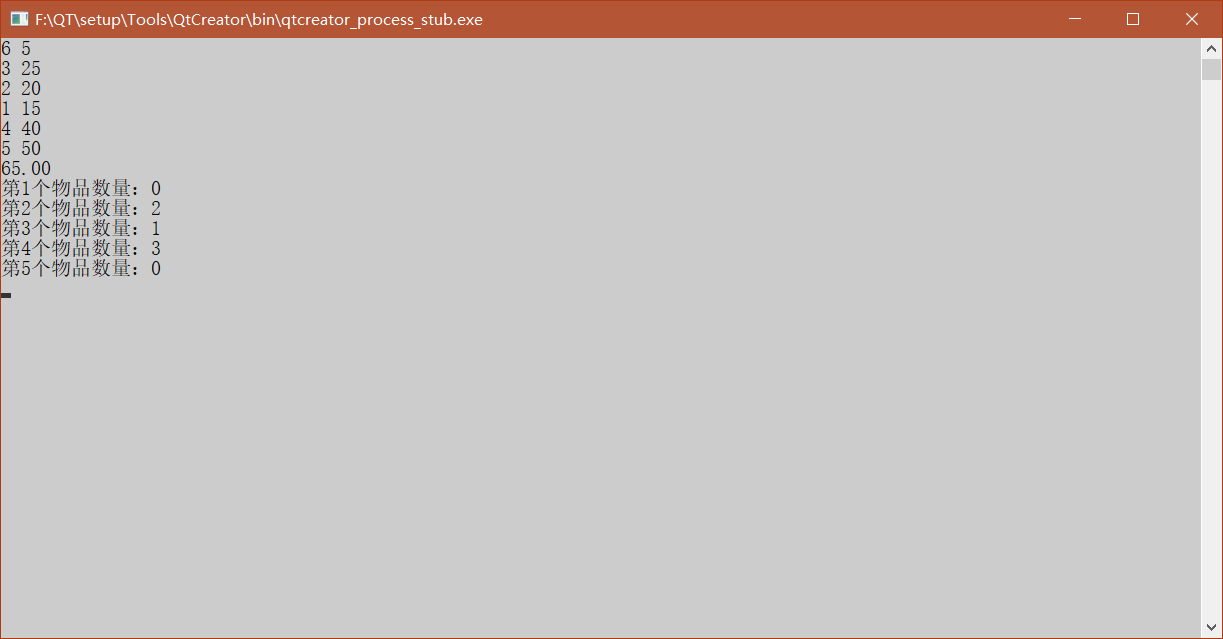
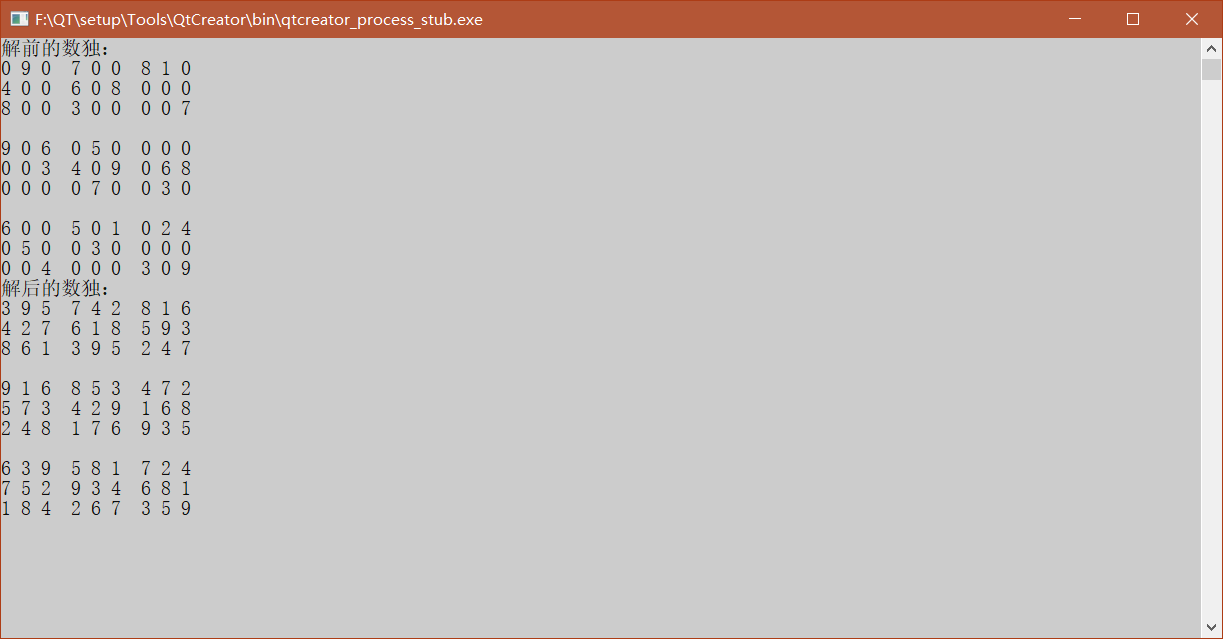
用所有算法解背包问题+数独问题。
二、所用算法的基本思想及复杂度分析:
1、0/1背包问题---蛮力法
1) 基本思想
对于每一种情况,我们用深度优先搜索遍历每一种情况,并记录其最大价值(每次有更大的就更新最大价值)。
2) 复杂度分析
T(n)=O(2n)。
2、0/1背包问题---分治法
1) 基本思想
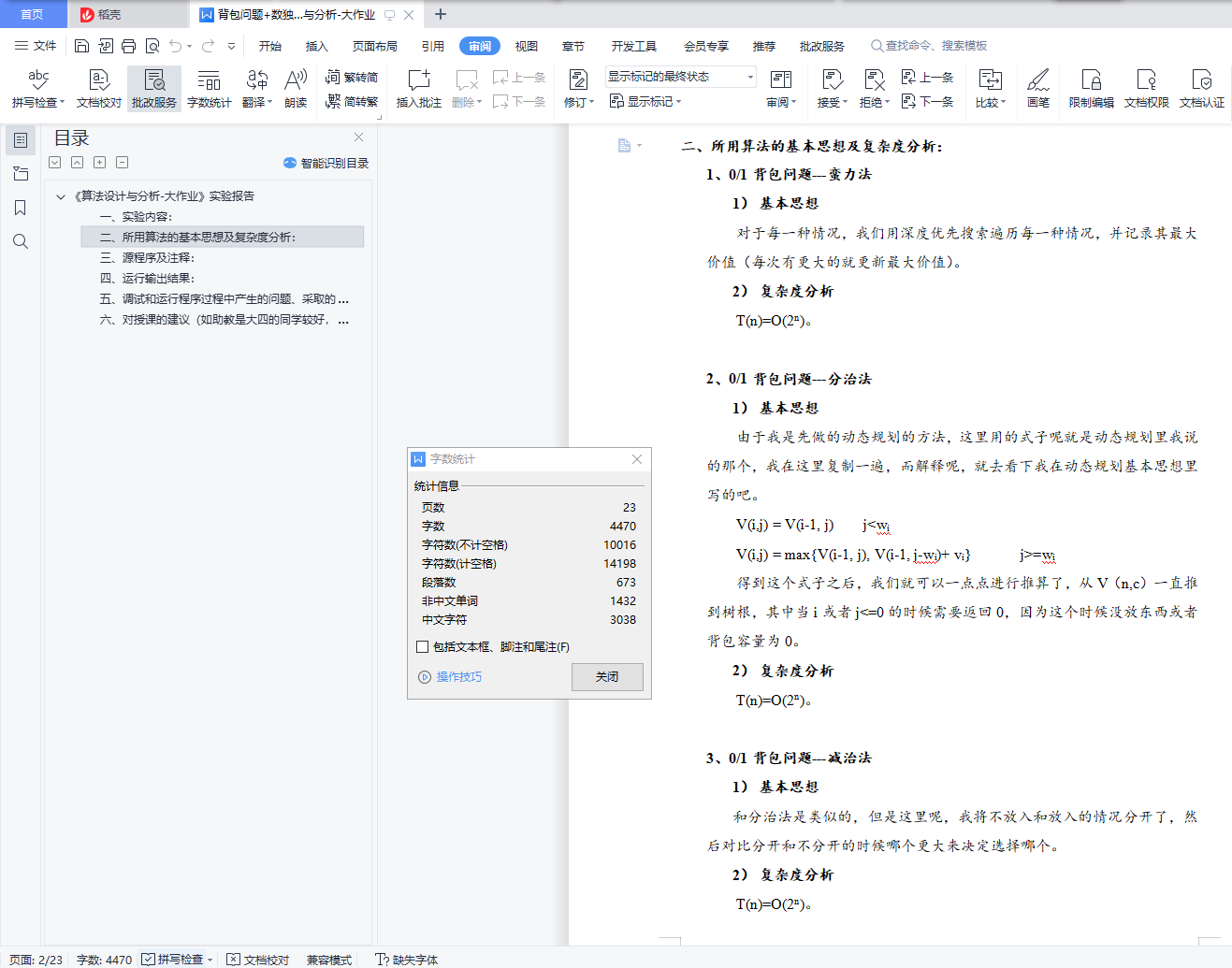
由于我是先做的动态规划的方法,这里用的式子呢就是动态规划里我说的那个,我在这里复制一遍,而解释呢,就去看下我在动态规划基本思想里写的吧。
V(i,j) = V(i-1, j) j<wi
V(i,j) = max{V(i-1, j), V(i-1, j-wi)+ vi} j>=wi
得到这个式子之后,我们就可以一点点进行推算了,从V(n,c)一直推到树根,其中当i或者j<=0的时候需要返回0,因为这个时候没放东西或者背包容量为0。
2) 复杂度分析
T(n)=O(2n)。
3、0/1背包问题---减治法
1) 基本思想
和分治法是类似的,但是这里呢,我将不放入和放入的情况分开了,然后对比分开和不分开的时候哪个更大来决定选择哪个。
2) 复杂度分析
T(n)=O(2n)。
4、0/1背包问题---动态规划法
1) 基本思想
我们依次求背包容量为v的时候能装下的最大价值value,直到达到最大值。
这里所谓的依次,也就是动态规划的思想,将这个大问题分解为一个个子问题,对于0/1背包问题,我们可以这样看:
首先,如果背包容量不足以装入第i个物品,那么背包总价值保持不变,也就是说,其价值仍然保持装入前i-1个物品的价值。
但是,如果背包容量足以装入第i个物品,那么这个时候我们就要考虑装入的时候和不装入的时候那种情况下能获得最大的价值。这里装入的情况即前i-1个物品装入容量为j-wi的背包中再加上第i个物品的价值,而不装入的情况和之前提到的那个等价。我们要做的就是取二者的最大值。