一、实验内容:
动态规划问题。
二、所用算法的基本思想及复杂度分析:
1、 01背包问题
1) 基本思想
我们依次求背包容量为v的时候能装下的最大价值value,直到达到最大值。
2) 复杂度分析
四个for循环,第一个是O(n),第二个是O(C),第三个是O(C*n),第四个是O(n),所以总的就是T(n)=O(C*n)。
2、 最长公共子序列
1) 基本思想
我们对这个问题可以分为很多子问题来进行求解,从末尾开始比较(也就是最小的那个子问题),如果相等,那么长度+1,如果不等那么考虑两个序列分别往前提一个之后公共长度谁最大,取最大的那个,依次往前推。
2) 复杂度分析
四个for循环,第一个是O(n),第二个是O(m),第三个是O(m*n),第四个是O(k)(k<=m,k<=n),所以总的就是T(n)=O(m*n)。
3、 K-近似匹配
1) 基本思想
我们考虑几种不同的情况,和最长公共子序列一样,从末尾开始,如果相同,则总差别数不变,不同或有一方多余则+1,不断递推即可。
2) 复杂度分析
两层for循环,T(n)=O(m*n)。
4、 最优二叉树查找
1) 基本思想
我们运用动态规划的方法,如果前n-1项构成最优二叉查找树,那么我们只要在这个基础上再考虑加入一个结点使之成为最优二叉查找树。
2) 复杂度分析
三层for循环,T(n)=O(n2)。
三、源程序及注释:
1、 01背包问题
2、 #include <iostream>
3、 #include <cmath>
4、 using namespace std;
5、
6、 int v_[10000][10000]; //前i个物品装入容量为j的背包中的最大价值
7、 int x[10000]; //装入背包的物品
8、
9、 int KnapSack(int w[], int v[], int n, int c){
10、 int i,j;
11、
12、 //初始化第0行和第0列
13、 for(i=0; i<=n; ++i)
14、 v_[i][0] = 0;
15、 for(j=0; j<=c; ++j)
16、 v_[0][j] = 0;
17、
18、 //计算第i行
19、 for(i=1; i<=n; ++i)
20、 for(j=1; j<=c; ++j)
21、 if(j<w[i])
22、 v_[i][j] = v_[i-1][j];
23、 else
24、 v_[i][j] = v_[i-1][j] > v_[i-1][j-w[i]]+v[i]
25、 ? v_[i-1][j] : v_[i-1][j-w[i]]+v[i];
26、
27、 //计算装入背包的物品
28、 for(j=c,i=n; i>0; --i)
29、 if(v_[i][j]>v_[i-1][j]){
30、 x[i] = 1;
31、 j = j-w[i];
32、 }else
33、 x[i] = 0;
34、
35、 //返回最大价值
36、 return v_[n][c];
37、 }
38、
39、 int main(){
40、 //w重量 v价值 n物品数 c背包容量
41、 int w[10000],v[10000];
42、 int n,c;
43、 cin>>n>>c;
44、 for(int i=1; i<=n; ++i)
45、 cin>>w[i]>>v[i];
46、 cout<<KnapSack(w,v,n,c);
47、 }
48、 最长公共子序列
49、 #include <iostream>
50、 #include <cmath>
51、 using namespace std;
52、
53、 int l[10000][10000]; //存储最长公共子序列长度
54、 int s[10000][10000]; //存储相应的状态
55、
56、 int CommonOrder(char x[], int m, char y[], int n, char z[]){
57、 int i,j,k;
58、
59、 //初始化0行0列
60、 for(j=0; j<=n; ++j)
61、 l[0][j] = 0;
62、 for(i=0; i<=m; ++i)
63、 l[i][0] = 0;
64、
65、 //计算
66、 for(i=1; i<=m; ++i)
67、 for(j=1; j<=n; ++j)
68、 if(x[i] == y[j]){
69、 l[i][j] = l[i-1][j-1]+1;
70、 s[i][j] = 1;
71、 }
72、 else if(l[i][j-1] >= l[i-1][j]){
73、 l[i][j] = l[i][j-1];
74、 s[i][j] = 2;
75、 }
76、 else{
77、 l[i][j] = l[i-1][j];
78、 s[i][j] = 3;
79、 }
80、
81、 //将公共子序列存储到z[k]中
82、 i = m;
83、 j = n;
84、 k = l[m][n];
85、 while(i>0 && j>0){
86、 if(s[i][j] == 1){
87、 z[k] = x[i];
88、 k--;
89、 i--;
90、 j--;
91、 }
92、 else if(s[i][j] == 2)
93、 j--;
94、 else
95、 i--;
96、 }
97、
98、 //输出最长公共子序列
99、 for(k=1; k<=l[m][n]; ++k)
100、 cout<<z[k];
101、 cout<<endl;
102、
103、 //返回公共子序列长度
104、 return l[m][n];
105、 }
106、
107、 int main(){
108、 //数组x长度m, 数组y长度n, 公共子序列存放在数组z
109、 char x[10000], y[10000], z[10000];
110、 int m, n;
111、
112、 cin>>m;
113、 for(int i=1; i<=m; ++i)
114、 cin>>x[i];
115、
116、 cin>>n;
117、 for(int i=1; i<=n; ++i)
118、 cin>>y[i];
119、
120、 cout<<CommonOrder(x,m,y,n,z);
121、 return 0;
122、 }
123、 K-近似匹配
124、 #include <iostream>
125、 #include <cmath>
126、 #include <algorithm>
127、 using namespace std;
128、
129、 int d[10000][10000];
130、
131、 int min(int a, int b, int c){
132、 int min = a<b?a:b;
133、 if(c<min)
134、 min = c;
135、 return min;
136、 }
137、
138、 int ASM(char p[], int m, char t[], int n){
139、 int i,j;
140、
141、 //初始化
142、 for(j=1; j<=n; ++j)
143、 d[0][j] = j;
144、 for(i=0; i<=m; ++i)
145、 d[i][0] = i;
146、
147、 //依次计算
148、 for(j=1; j<=n; ++j)
149、 for(i=1; i<=m; ++i)
150、 if(p[i-1] == t[j-1])
151、 d[i][j] = min(d[i-1][j-1], d[i-1][j]+1, d[i][j-1]+1);
152、 else
153、 d[i][j] = min(d[i-1][j-1]+1, d[i-1][j]+1, d[i][j-1]+1);
154、
155、 //返回最小差别数
156、 return d[m][n];
157、 }
158、
159、 int main(){
160、 //p[]存储模式 t[]存储文本
161、 char p[10000],t[10000];
162、 int m,n;
163、
164、 cin>>m;
165、 for(int i=1; i<=m; ++i)
166、 cin>>p[i];
167、
168、 cin>>n;
169、 for(int i=1; i<=n; ++i)
170、 cin>>t[i];
171、
172、 cout<<ASM(p,m,t,n);
173、 return 0;
174、 }
175、 最优二叉树查找
176、 #include <iostream>
177、 #include <cmath>
178、 #include <algorithm>
179、 using namespace std;
180、
181、 double c[10000][10000];
182、 double r[10000][10000];
183、
184、 double OptimalBST(double p[], int n){
185、 int i,j,k,d;
186、 double min,mink,sum;
187、
188、 //初始化主对角线和第一条次对角线
189、 for(int i=1; i<=n; ++i){
190、 c[i][i-1] = 0;
191、 c[i][i] = p[i-1];
192、 r[i][i] = i;
193、 }
194、 c[n+1][n] = 0;
195、
196、 //计算其余对角线
197、 for(d=1; d<n; ++d)
198、 for(i=1; i<=n-d; ++i){
199、 j = i+d;
200、 min = 9999;
201、 mink = i;
202、 sum = 0;
203、 for(k=i; k<=j; ++k){
204、 sum += p[k-1];
205、 if(c[i][k-1]+c[k+1][j]<min){
206、 min = c[i][k-1]+c[k+1][j];
207、 mink = k;
208、 }
209、 }
210、 c[i][j] = min+sum;
211、 r[i][j] = mink;
212、 }
213、
214、 ////////////////////////////
215、 for(i=0; i<=n; ++i){
216、 for(j=0; j<=n; ++j)
217、 cout<<c[i][j]<<"\t";
218、 cout<<endl;
219、 }
220、
221、
222、 return c[1][n];
223、 }
224、
225、 int main(){
226、 //n个字符的查找概率存储在p[]中
227、 double p[10000];
228、 int n;
229、
230、 cin>>n;
231、 for(int i=0; i<n; ++i)
232、 cin>>p[i];
233、
234、 cout<<OptimalBST(p,n);
235、 }
四、运行输出结果:
1、 01背包问题
2、 最长公共子序列
3、 K-近似匹配
4、 最优二叉树查找
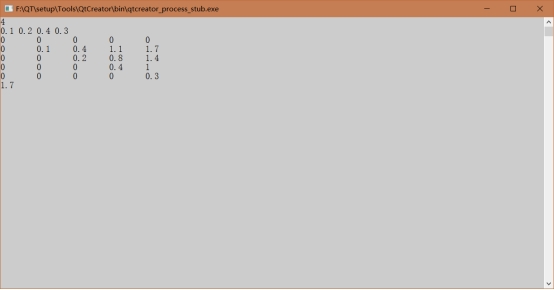
五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训:
1、我一开始把二叉查找树那里的一些数据类型搞错了,导致出现了一些错误(数据类型不匹配)。



