一、实验内容:
分治减治问题。
二、所用算法的基本思想及复杂度分析:
1、 最近点对问题
1) 基本思想
首先,对多个点的中间进行划分,通过递归求左右两边的最近点对距离,比较后得出左右两边最近点对距离更小的那个,记为d。
接着,在横坐标-d~d之间查找最近点对距离,如果小于d则d取新的值。
最终得到最近点对距离为d。
2) 复杂度分析
由于存在如下递推式:
T(n) = 1; k=2
T(n) = 2T(n/2)+n; k>2
由上上次作业可知,复杂度为O(nlog2n)
2、 减治法求an
1) 基本思想
将an中的n分三种情况讨论,则an=
a; n=1
(an/2)2; n为偶数且n!=1
(a(n-1)/2)2*a; n为奇数且n!=1
然后递归求解。
2) 复杂度分析
由上式显得易得,复杂度为O(log2n)
三、源程序及注释:
1、 1、最近点对问题
2、 #include <iostream>
3、 #include <math.h>
4、 using namespace std;
5、
6、 //点
7、 struct point{
8、 int x,y;
9、 void setPoint(int sx, int sy){
10、 x = sx;
11、 y = sy;
12、 }
13、 };
14、
15、 //距离
16、 double Distance(point a, point b){
17、 return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
18、 }
19、
20、 //调整序列,大的放右边 小的放左边
21、 int adjust(point a[], int front, int rear){
22、 int i=front, j=rear;
23、 int y = a[front].y;
24、 int x = a[front].x;
25、 while(i<j){
26、 while(a[j].y>=y && i<j)
27、 j--;
28、 a[i].x = a[j].x;
29、 a[i].y = a[j].y;
30、 while(a[i].y<=y && i<j)
31、 i++;
32、 a[j].x = a[i].x;
33、 a[j].y = a[i].y;
34、 }
35、 a[i].y = y;
36、 a[i].x = x;
37、 return i;
38、 }
39、
40、 //快速排序(y坐标升序排列)
41、 void quickSort(point a[],int front, int rear){
42、 if(front<rear){
43、 int empty = adjust(a,front,rear);
44、 quickSort(a,front,empty-1);
45、 quickSort(a,empty+1,rear);
46、 }
47、 }
48、
49、 point P[100000]; //存放集合
50、
51、 //求最近点对
52、 double closest(point s[], int low, int high){
53、 double d1,d2,d3,d;
54、 int mid,i,j,index;
55、 // point P[high+1]; //存放集合
56、
57、 //处理左右两边的点的最小点对
58、 //两点 求距离
59、 if(high-low==1)
60、 return Distance(s[low],s[low+1]);
61、 //三点 求最近点对
62、 if(high-low==2){
63、 d1 = Distance(s[low],s[low+1]);
64、 d2 = Distance(s[low+1],s[high]);
65、 d3 = Distance(s[low],s[high]);
66、 if(d1<d2 && d1<d3)
67、 return d1;
68、 else if(d2<d3)
69、 return d2;
70、 else
71、 return d3;
72、 }
73、 //中间点
74、 mid = (low+high)/2;
75、 //递归求左边最近点对
76、 d1 = closest(s,low,mid);
77、 //递归求右边最近点对
78、 d2 = closest(s,mid+1,high);
79、
80、 //取左右两边最小点对值
81、 if(d1<=d2)
82、 d = d1;
83、 else
84、 d = d2;
85、 index = 0;
86、
87、 //求中间 -d~d最近点对
88、 //保存左边点对 左边 -d~0
89、 for(i=mid; i>=low && (s[mid].x-s[i].x)<d; --i)
90、 P[index++] = s[i];
91、 //保存右边右边 0~d
92、 for(i=mid+1; i<=high && (s[i].x-s[mid].x)<d; ++i)
93、 P[index++] = s[i];
94、 //按y升序排序
95、 quickSort(P,0,index-1);
96、 //处理
97、 for(i=0; i<index; ++i){
98、 for(j=i+1; j<index; ++j){
99、 if(P[j].y-P[i].y >= d)
100、 break;
101、 else{
102、 d3 = Distance(P[i],P[j]);
103、 if(d3<d)
104、 d = d3;
105、 }
106、 }
107、 }
108、 return d;
109、 }
110、
111、 int main()
112、 {
113、 int num;
114、 cin>>num;
115、 while(num--){
116、 point s[100000];
117、 int n;
118、 cin>>n;
119、 for(int i=0; i<n; ++i){
120、 int x, y;
121、 cin>>x>>y;
122、 s[i].setPoint(x,y);
123、 }
124、 printf("%.2lf\n",closest(s,0,n-1));
125、 }
126、
127、 }
3、 2、减治法求an
4、 //减治法求 a^n
5、 #include <iostream>
6、
7、 using namespace std;
8、 #include <cmath>
9、
10、 double an_DecCon(int a, int n){
11、 if(a==0)
12、 return 0;
13、 if(n==1)
14、 return a;
15、 else if(n%2 == 0){
16、 return pow(an_DecCon(a,n/2),2);
17、 }else{
18、 return pow(an_DecCon(a,(n-1)/2),2)*a;
19、 }
20、 }
21、
22、 int main()
23、 {
24、 int a,n;
25、 cin>>a>>n;
26、 cout<<an_DecCon(a,n);
27、 }
四、运行输出结果:
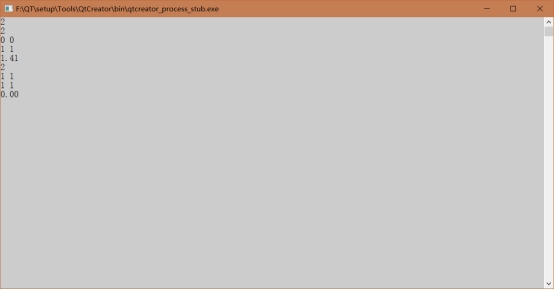
最近点对问题:
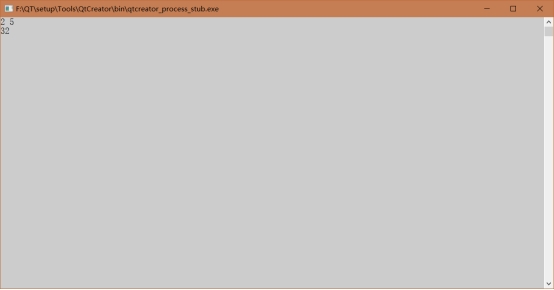
减治法求an
五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训:
1、一开始求an没有考虑到a=0的情况
2、最近点对问题将大数组定义在函数内部,导致运行效率低下,在oj中会出现runtime error错误,最后我将其声明为全局变量。



