题目一 使用回溯法解决Akari问题

一、目的

1. 了解Akari问题，探索其解决方法；

2. 了解回溯法的概念，掌握回溯法的原理，并能够使用一种编程语言通过使用回溯法解决问题；

3. 培养和锻炼分析问题与解决问题的能力。

二、基本原理

1． Akari问题

Akari问题有时又被称为Light up或者Beleuchtung，源于日本逻辑解密游戏系列Nikoli，同属于Nikoli谜题的除Akari之外还有Sudoku(数独)和Kakuro(数谜)等。

Akari问题要求在一定大小的棋盘上放入一定数量的“车”，并满足以下条件：

（1） “车”只能放在白色格子里，不能放在黑色格子里；

（2） 黑色的格子会挡住“车”的攻击；

（3） 所有的“车”不能相互攻击；

（4） 若一个黑色的格子里有数字，则与其相邻的4个格子（上下左右方向）中的车的数量与该数字相同；

（5） “车”需要“覆盖”棋盘上所有的白色格子，换言之，所有未放入“车”的白色格子都要被“车”所能攻击到；

Akari问题的示意如图1所示。

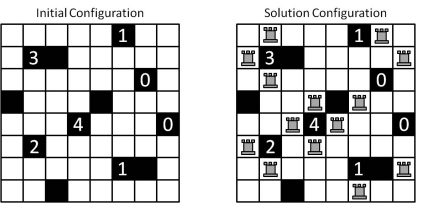
图1 Akari的初始状态与解

2.  回溯法

回溯法是一种迭代算法。在回溯法中，首先将问题的解决分为若干步，其次通过枚举每一步的选择构造解空间树。在此基础上通过深度优先搜索遍历此解空间树，若当前节点的局部解不能构造出全局解，则向上回溯，否则向下扩展。重复此步骤直到找到全局解。

回溯法的关键点在于：

第一，问题可分步并且可枚举每一步的选择。

第二，可以迅速的判断出当前局部解可否构造出全局解。

若问题可分为N步，每一步有M种选择，易知其时间复杂度为O(pow(m,n))，虽然和穷举法有着相同的时间复杂度，但因为是逐步搜索并不断摒弃局部解，因此在实际应用中比穷举法效率高的多。

回溯法的递归形式的伪代码如下。

三、实验数据

实验数据由若干TXT文件组成，每个文件描述一个Akari问题的初始状态，编写程序读入此TXT文件，根据初始状态求解。有的TXT文件没有解，有的有一个解，有的有多个解。

TXT文件由若干行组成，第一行为两个整数，代表棋盘的行数和列数。第二行开始为若干字符，并用空格进行分割。其中按顺序每3个字符构成一个三元组（X，Y，Z）的形式，每个三元组代表棋盘中的一个黑色格子。其中X代表行标，为英文小写字母，从a开始；Y代表列标，为阿拉伯数字，从0开始；Z代表黑色格子中的数字，若为‘X’则表示该格子中没有数字。没有被三元组表示的格子为白色格子。一个TXT文件的示例内容如图2所示。

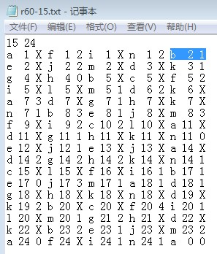
图2 程序输入文件的示意图

四、内容及步骤

编程实现使用回溯法解决Akari问题。要求首先对问题进行划分，并根据每一步构造解空间，进而设计合理的数据结构与程序结构对问题进行求解，并在此基础上对算法以及程序逻辑进行优化和改进，最后进行问题的分析、讨论和展望。关键步骤如下。

1. 对问题进行划分

根据黑色方格中数字的大小，按从大到小的顺序进行排序，并将“在一个有数字的黑色方格周围放置‘车’”定义为一步。

2. 选择枚举

枚举每一步的选择。

若黑色方格中的数字为4，则其相邻的周围格子的“车”的放置方式为1种，即上下左右均放置一个“车”。

若黑色方格中的数字为3，则其相邻的周围格子的“车”的放置方式为4种，即在左右下、下右上、右上左、上左下的格子中放置“车”。

若黑色方格中的数字为2，则其相邻的周围格子的“车”的放置方式有6种，即在上左、上下、上右、左下、左右、下右的格子中放置“车”。

若黑色方格中的数字为1，则其相邻的周围格子的“车”的放置方式有4种，即在上、下、左、右的格子中放置“车”。

若黑色方格中的数字为0，则其相邻的周围格子中的“车”的放置方式有1种，即所有周围格子均不放置车。

3. 构造解空间

根据上述讨论构造解空间，初始状态为解空间树的根节点，从编号最大的黑色格子开始尝试填入“车”，填入后判断是否为一个可行解，若为可行解，则解空间向下进行分枝，否则向上进行回溯。解空间树的结构大致如图2所示。

4. 程序设计与实现

根据回溯法的伪代码和上述算法的设计思路，建立合适的数据模型与程序结构，编写程序求解问题，同时记录程序的运行时间。

5. 讨论与改进

分析算法的时间负责度与空间复杂度，根据某一用例和计算机的计算能力，估计程序运行时间，并将该时间与实际运行时间进行比较。

同时讨论与优化程序结构和数据结构，以求达到更快的程序执行速度和更少的内存占用量。

一种可能的解空间如图3所示。

图3 解空间树的结构

五、思考题

1． 回溯法和分支限界法在算法上有一定的相似性，将本题使用分支限界法来进行求解可否提高程序运行速度？为什么？

2． 算法把黑色格子按从大到小的顺序进行排列，并按此顺序填入“车”，为什么？

3． 如果以解空间的节点数量为判断标准，可否有更好的划分问题与枚举选择的方法？如果有，为什么这个方法比原方法要好？

六、写作大纲与格式

附A：部分读取序列数据的源代码

c、perl、Java

题目二 使用并行回溯法求解Akari问题

一、目的

1． 掌握串行程序并行化的方法；

2． 熟悉在Linux的C++语言环境下进行并行程序设计的方法；

3． 了解了解并行程序设计与并行算法设计的基本分析方法与途径。

二、基本原理

1．Akari串行回溯算法的并行化

串行算法并行化的过程中的核心问题是问题分解和解除数据相关的问题。所谓的问题分解问题即将串行算法采取分治的理念分成可并行计算的子问题，解除数据相关的问题就是采取一定的冗余策略或锁策略使各子问题的私有数据之间不相互影响。

回溯法是易于并行化的典型算法之一，在Akari问题的回溯算法中，可以清楚的认识到回溯的具体路线的选择对产生解的正确性没有影响，因此该回溯法中每个节点的计算过程以及节点的分裂过程均是可以并行计算的。同时由算法的性质决定了每个解空间节点各自数据不会相互影响，没有任何数据相关。并行的Akari回溯算法的示意图如图4所示。

图4 Akari问题的并行解空间

图中彩色的矩形表示可以并行执行的单元，可以看出，解空间树中相同层的执行是可以并行化的，不同层之间的执行依然可以并行化。

2. Linux下C++环境中并行编程方法

(1) 使用pthread进行多线程编程

POSIX thread 简称为pthread，是一个支持POSIX的标准线程，该标准定义内部API用于创建和操纵线程。POSIX是指可移植性操作系统接口（Portable Operating System Interface），被大多数操作系统支持（如Unix，Linux，Windows），其编程方式简单易用并且可移植。

在Linux下使用pthread多线程需要在使用gcc/g++的时候加上lpthread编译选项，以便使链接器能动态链接到pthread库。

(2) 使用fork()进行多进程编程

在Linux环境下，一个现有进程可以调用fork函数创建一个新进程。由fork创建的新进程被称为子进程（child process）。fork函数被调用一次但返回两次。两次返回的唯一区别是子进程中返回0值而父进程中返回子进程ID。

子进程是父进程的副本，它将获得父进程数据空间、堆、栈等资源的副本。注意，子进程持有的是上述存储空间的“副本”，这意味着父子进程间不共享这些存储空间。

使用fork()系统调用可在Linux实现并行编程，但相对于pthread来说创建新的进程开销要大于新的线程。

三、实验数据

实验数据由若干TXT文件组成，每个文件描述一个Akari问题的初始状态，编写程序读入此TXT文件，根据初始状态求解。有的TXT文件没有解，有的有一个解，有的有多个解。

TXT文件由若干行组成，第一行为两个整数，代表棋盘的行数和列数。第二行开始为若干字符，并用空格进行分割。其中按顺序每3个字符构成一个三元组（X，Y，Z）的形式，每个三元组代表棋盘中的一个黑色格子。其中X代表行标，为英文小写字母，从a开始；Y代表列标，为阿拉伯数字，从0开始；Z代表黑色格子中的数字，若为‘X’则表示该格子中没有数字。没有被三元组表示的格子为白色格子。

四、内容及步骤

根据上述分析，设计并行化的回溯算法，并用其解决Akari问题。在Linux环境下使用C/C++语言编程实现，同时测量算法执行时间，并计算加速比。

1． 确定并行粒度

确定并行粒度也就是把算法中可并行执行的单元映射到不同task的过程。一个可行的映射方法如图5所示。

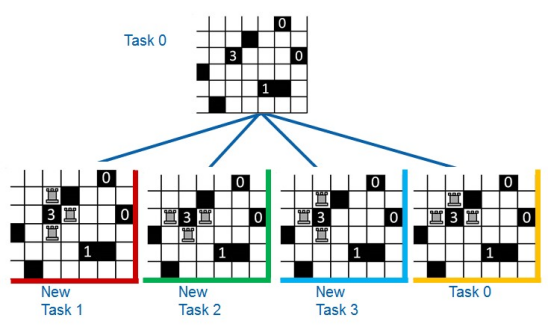
图5 一种task的映射方法

2． 使用并行程序设计方法实现算法

使用pthread将task映射到thread或者使用fork将task映射到不同的进程。设计新的数据结构来适应并行化的编程需要。

3． 测量时间并计算加速比

运行新的并行程序，测量程序运行时间，并与实验1中的串行运行时间相比较，计算出并行程序的加速比。

五、思考题

1． 除了实验中给出的串行程序并行化方法外，针对此Akari问题，你是否还有更好的并行程序设计方法。

2． 使用阿姆达尔定律计算出的理想加速比与实际测得的加速比有一定的差距，这是由于开销造成的，请结合操作系统原理说明，在实验中产生的开销具体是什么？并提出减少开销的方法。

六、写作大纲与格式

要求：

1． 画出程序流程图，并对关键数据结构进行说明，同时附上关键性代码；

2． 运行程序多次计算运行时间，并和串行程序相比计算出加速比；

3． 回答思考题。

题目三 使用改进的并行回溯法求解Akari问题

一、目的

1． 掌握优化并行程序的方法；

2． 了解并行粒度与性能之间的关系，掌握通过并行粒度分析程序性能的方法；

3． 了解并行程序设计与并行算法设计的基本分析方法与途径。

二、基本原理

1．并行计算中的粒度与性能

多线程应用的并行任务工作量大小（粒度）会对其并行性能产生很大影响。在分解一项应用使之适用于多线程处理时，编程时通常采用的方法是从逻辑上将问题分割成尽量多的并行任务，或者在并行任务内根据共享数据与执行顺序决定进行哪些必要的通信。由于分割任务、将任务分配给线程以及在任务之间进行数据通信（共享）涉及到一定的成本，编程者通常需要聚合或整合分割的任务，用于避免随之产生的开销，尽量实现应用高效运行。通过聚合分割的任务可确定并行任务的最佳粒度。
   粒度通常与工作负载在线程之间的均衡程度有关。尽管平衡大量小型任务的工作负载更容易，但这样做却可能导致通信和同步等方面的并行开销过高。此时，编程者可以通过将小型任务整合成一项任务，增加每项任务的粒度（工作量）来减少并行开销。

2．并行回溯法求解Akari问题时的并行粒度划分方法

并行粒度的划分实质上是一个将工作负载（任务）与工作单元（线程或进程）对应的过程，在本实验过程中，对于Akari问题的粒度划分方法有以下几种：

（1） 每个解空间的节点分裂均产生新任务

（2） 当且仅当解空间树节点第一次分裂的时候产生新任务

（3） 当且仅当解空间树节点在数字“3”的时候分裂时产生新任务

三、实验数据

实验数据由若干TXT文件组成，每个文件描述一个Akari问题的初始状态，编写程序读入此TXT文件，根据初始状态求解。有的TXT文件没有解，有的有一个解，有的有多个解。

TXT文件由若干行组成，第一行为两个整数，代表棋盘的行数和列数。第二行开始为若干字符，并用空格进行分割。其中按顺序每3个字符构成一个三元组（X，Y，Z）的形式，每个三元组代表棋盘中的一个黑色格子。其中X代表行标，为英文小写字母，从a开始；Y代表列标，为阿拉伯数字，从0开始；Z代表黑色格子中的数字，若为‘X’则表示该格子中没有数字。没有被三元组表示的格子为白色格子。

四、内容及步骤

根据上述分析，设计并行化的回溯算法，并用其解决Akari问题。在Linux环境下使用C/C++语言编程实现，同时测量算法执行时间，并计算加速比。

1． 确定并行粒度

根据公式推导和理论计算，在实验所给并行粒度中选取最合适的并行粒度。

2． 使用并行程序设计方法实现算法

使用pthread将task映射到thread或者使用fork将task映射到不同的进程。设计新的数据结构来适应并行化的编程需要。

3． 测量时间并计算加速比

运行新的并行程序，测量程序运行时间，并与实验1中的并行运行时间相比较，计算出并行程序的加速比。

根据数据和计算结果，思考分析不同的并行粒度对并行计算性能的影响。

五、 思考题

1． 实验中所给的并行粒度是最优的吗？如果不是，尝试使用方法找出最佳的并行粒度并说明原因。

2． 并行粒度对性能的影响很大一部分是因为各工作单元的负载不均衡造成的，在本题中，可否设计一种算法或者机制，根据各回溯的情况，动态调整并行粒度，达到更好的负载均衡？

六、写作大纲与格式

要求：

1． 简述实验的目的及原理；

2． 说明哪种并行粒度划分的最合适；

3． 画出程序流程图，并对关键数据结构进行说明，同时附上关键性代码；

4． 运行程序多次计算运行时间，并和串行程序相比计算出加速比；

5． 回答思考题。