梁的弯曲的分析与设计

5.1简介

本章与下一章绝大部分内容将专门分析和梁的设计，即结构构件支撑负载。在沿构件的各点施加。梁通常是长，直棱柱构件，如图所示的前面的照片中。钢梁和铝梁这两个结构在机械工程发挥重要作用。木梁被广泛应用于家园建设（图片5.1）。在大多数情况下，负载垂直于梁的轴线。这种横向荷载在梁中引起唯一弯曲和剪切。当负载作用于不正确的角梁，他们也在梁中产生的轴向力。

图片5.1 木梁的使用

一个梁的横向载荷可由两个载荷P1，P2。它们用牛顿，磅，或它们的倍数， 千牛顿和千磅来表示，或者它们俩者都用。当负载W在部分单位长度具有一个常数值的均布荷载（如A与B在图5.1中），可以说负载被被均匀地分布在梁的一部分。梁根据它们这样的分类分为几类。几种类型的梁示于图5.2。

静定梁

a 简支梁             b 悬挑梁           c 悬臂梁

超静定梁

a 连续梁            b 一端固定梁       c 固定梁

在该图5.2中的各个部分中所示的距离L被称为跨度。注意，该梁反应的支撑在零件A，B，和C中的数字的总共只有三个未知数，因此，可通过静力学的方法测定。这样被说成是静定梁，这一章和下一章将要讨论它。另一方面，弯曲反应在在梁的部分D，E和F所示的梁的支承。涉及较多未知数且超过三个，并且不能由方法来测定独自静定的。梁自己具有的抗变形必须予以考虑。这样被称为梁的超静定，它们的分析将被推迟到第一章.9在那里梁的变形将讨论。

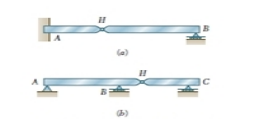
通过铰链连接的梁

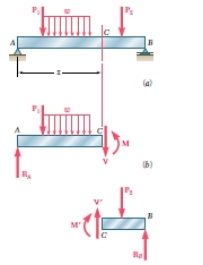
有时两个或更多的梁被铰链连接到形成一个单一的连续结构。梁的两个例子铰接在点H示于图5.3 。将指出的是，反应包括连续结构之内有四个未知数，无法确定从双梁系统的自由体图。它们可以这样决定，认识到在内部铰链内力是零。然后，考虑到每个的自由体图后束分开， 6个未知数（其中包括两个力在铰链组件）和6方程是可用的。当一梁有横向载荷时，内部在梁的任何截面力通常将包括一个剪切力V和弯矩M都要考虑，例如，一个简单的支梁AB有着两个集中载荷和均匀分布荷载（图5.4A ） 。要确定内力的部分通过C点，我们先绘制的自由体图整个光束，以获得载体的反应（图5.4B ） 。通过C点，我们再画形成的自由体图

（图5.4c ） ，从中我们确定的剪切力V和弯矩M.在横截面的弯矩m创建正应力，而剪力V中的部分创建剪切应力。

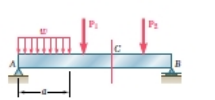
横装梁

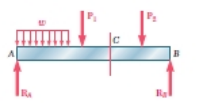
自由体的支撑

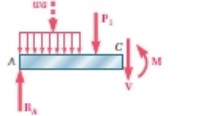
自由体内力图C

在大多数情况下，在一个梁的设计的主要判据梁的应力强度的最大值。该确定在一个梁的正常应力将在这一章讨论，而剪切应力将在11.2节中讨论， 因为一般压力在给定部分中的分布在该部分中的弯矩M的值取决于和截面的几何形状， 弹性挠曲公式由章节4.4可用于确定最大应力，以及应力在任何给定的点，在该部分。我们写

σm=|m|c/I     σx=My/I

其中I是相对于横截面的惯性矩以垂直于两个平面的形心轴， y是从中立面，和c的距离的最大值那距离（图4.11 ） 。我们还记得在章节4.4中，引入弹性截面模数S=i/c，在本节中的正应力的最大值每平方米可表示为

σm=|M|/s

截面模数各种选择，型材见附录C，而矩形形状的截面模量可以表示，如图所示在章节4.4如

S=1/6*bh²

其中b和h分别是宽度和横的。方程（5.3）还表明，对于均匀的梁， SM是成正比求| M |最大值 因此，该最大值发生在梁正应力最大的地方，| M |是最大的。判定该位置遵循的设计中最重要的部分之一是梁对于给定的荷载条件和最大弯矩幅度。绘制一个弯矩图表更容易得出结论，即，如果该弯曲力矩M的值在不同的测定梁的点和作图从测得的距离x梁的一端。它是进一步促进了如果在同一时间剪切图是通过绘制对x的剪切从而绘制剪力V，可用于记录的值的符号约定剪力和弯矩将在章节5.2进行讨论，V和M然后将各点的梁绘制获得梁的连续部分自由体图。在秒。负载，剪切和弯曲力矩之间的关系在章节5.3将导出，并可以认识剪切和弯矩图的绘制。这种方法有利于求弯矩最大绝对值的值，将由此，判定最大正应力在梁的哪里。在章节5.4您将学习如何设计一个梁的弯曲，即，所以该梁的最大正应力不超过其允许值。正如前面所指出的，这是主要的判据在梁的设计确定最大值的另种方法。在剪切和弯曲力矩的基础上，表示V和M在 的函数方面的关系，将在章节5.5中讨论，这 方法非常适用于使用电脑，并将于扩大计算，方便坡度的判断和偏转梁。 最后变形截面梁的设计，也就是说，梁以可变的横截面，将在章节5.6中讨论可变横截面的形状和尺寸，使得其弹性剖面模数S沿着梁的长度而改变相同的| M |，它可以设计梁的量，在每个区段的最大正应力等于允许的应力的材料制成。据说这种梁是恒定的强度。

5.2剪切和弯曲，弯矩图

在一个梁的弯曲力矩的剪力之和的值都大大缩短，如果V和M分别从梁的一端作图测得距离x。此外，正如你将在第一章看到。如图9所示，力矩M知识作为x的函数是必不可少的判定梁的偏转。本节中的示例和示例的问题，剪切和弯曲力矩图表将确定获得V和M'中的梁的所选点中的值。这些值将按照常规的方式求出，即，通过使截面通过他们的位置确定（图5.5A ）和点到梁的所述部分位于上的平衡两侧的部分（图5.5B ）的距离。由于剪切力V和V*有相反的感觉，记录剪力在C点用了向下箭头就毫无意义，除非我们在表示其中AC和CB时候，我们考虑用。出于这个原因，在剪切V将带符号：一个加符号，如果剪切力被定向一个加符号，如果剪切力被定向，如图所示5.5用一个负号表示，否则。类似的公约将适用于

的弯曲力矩M。它会被认为是可用的，如果弯矩图所示，否则负号已证明， 总结出后我们提出符号约定，我们可以说：剪力V和在给定点处的弯矩M梁说是正值当内力和梁的各部分被定向为如图所示。 5.6A 。这些结论可以更容易地记住，如果我们注意。在任何给定的点到梁的剪切为正时外力（荷载和反应）作用在横梁上倾向于以剪除所述梁在这一点上，如图所示。

5.6B  a   V和M的测定

a 内力（正剪力和正弯矩） b外部力的影响（正剪力） c外力的影响（正弯矩）

弯矩在任何给定点的梁是正当作用下在横梁上的外力容易弯曲，梁的弯曲图表示了这一点。还需要注意的是这种情况在图5.6中描述， 在该弯矩的剪切和的值都正，恰恰发生在一个左半部的简支梁承载单一的集中荷载的中点。这种特殊的情况下是在例题中讨论。

5.3 负载 剪力和弯矩之间的关系

当梁携带超过两个或三个集中荷载，或者当它承载均布荷载，在第 5.2章节用于绘制剪力和弯矩的方法是相当繁琐的。剪力图，特别是构建弯曲弯矩图将极大便利，如果现有的负载，剪力和弯曲力矩有一定的关系，让我们考虑采取一个简支梁AB背着一个均布荷载w每单位长度（图5.11A ） ，并让C和C*是两个梁在彼此的距离相等的点。剪切和弯矩将会由V和M分别表示。;在C*的剪力和弯矩会由△V和△M表示。我们现在分离梁C*的部分，并画出它的自由体图（图5.11B ）。施加在自由体的力量包括负荷的大小w和C和C*的内力 。由于剪力和弯矩并已假设成立，力和弯矩将被引导，如图所示。，剪力之间的关系有

+↑∑Fy=0  V-(V+△V)-w△x=0

△V=-w△x

用DX除以方程的两方程的结果，然后让DX接近零，我们得到

dV/dx= -w

等式（5.5）表示，对于如图。 5.11A，剪切曲线的斜率dV/dx为负，斜率的数值在任何点等于每单位长度的负载在该 点C和D之间的积分，我们

Vd-Vc=-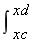wdx

Vd-Vc=-(area under load curve between CandD)

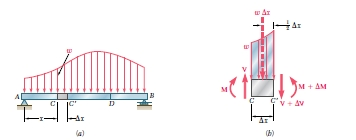
简支梁受荷载分布

注意，这结果也考虑了梁C D部分的平衡，根据该区域负载曲线表示C和D之间施加的总载荷 ，但应指出，方程（5.5）有无效的点处是 其中一个集中荷载;剪切曲线是不连续的 在这样一个点，如章节5.2所示，同样地，方程（5.6）和 （5.69）施加集中荷载 C和D不再有效，因为它们没有考虑到在剪切引起的集中负荷的突然变化等式（5.6）和（5.69），因此，应该只应用于之间连续负载。剪力和弯矩之间的关系。回到图5.11中，在C’上的总和为0。所以我们有

+↑∑Mc=0:      (M+△M)-M-V△X+w△X*△X/2=0

△M=V△X-0.5△X²

等式（5.7）表示该弯矩的斜率dy/dx 曲线是相等的剪切值。这是真实的任意点，其中剪切具有定义的值，即在任何点，其中没有集中施加负荷。方程（5.7）还表明，在V=0的点，其中M为最大。此属性有助于确定该点所在的梁很可能在弯曲的部位。点C和D之间的积分（5.7），我们写

Dm/dx=V

Md-Mc=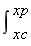Vdx

需要注意的是，剪切曲线下的面积，应考虑位置其中的剪切是正和负，其中剪切为负。 方程（5.8）和（5.89）是有效的集中荷载，即使负载C和D之间施加，只要在剪切曲线具有被正确绘制，方程不再为有效的，但是如果一个弯矩被应用在C和D之间的一个点，因为他们不采取考虑到在弯矩的突然变化造成的影响。

在大多数工程应用中，人们仅需要在一些特别的点知道弯矩。一旦剪力图已经绘就，和弯矩M已确定后，在一个梁的端部求该弯曲力矩的值 然后，可以通过计算面积在任意给定点获得 下的剪切曲线。例如例5.03中的最大值 可以通过测量获得简单弯矩为梁在图1的剪切图中的阴影三角形的面积。我们在例中有：

Mmax=Wl²/8

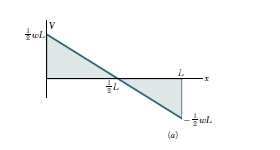
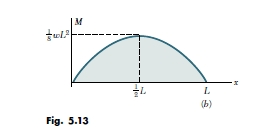
我们注意到，在这个例子中，负载曲线是水平直线，剪切曲线的斜直线，并且M是曲线的抛物线。