B+树 BulkLoading 多核并行设计
目录
数据库系统课程设计报告
B+树 BulkLoading 多核并行设计
Ⅰ . B+树 BulkLoading 过程理解
1.1 BulkLoading 的基本思想
1.2 结合实现理解 BulkLoading
1.3 BulkLoading 的利弊
Ⅱ . 并行设计思路
2.1 基本想法
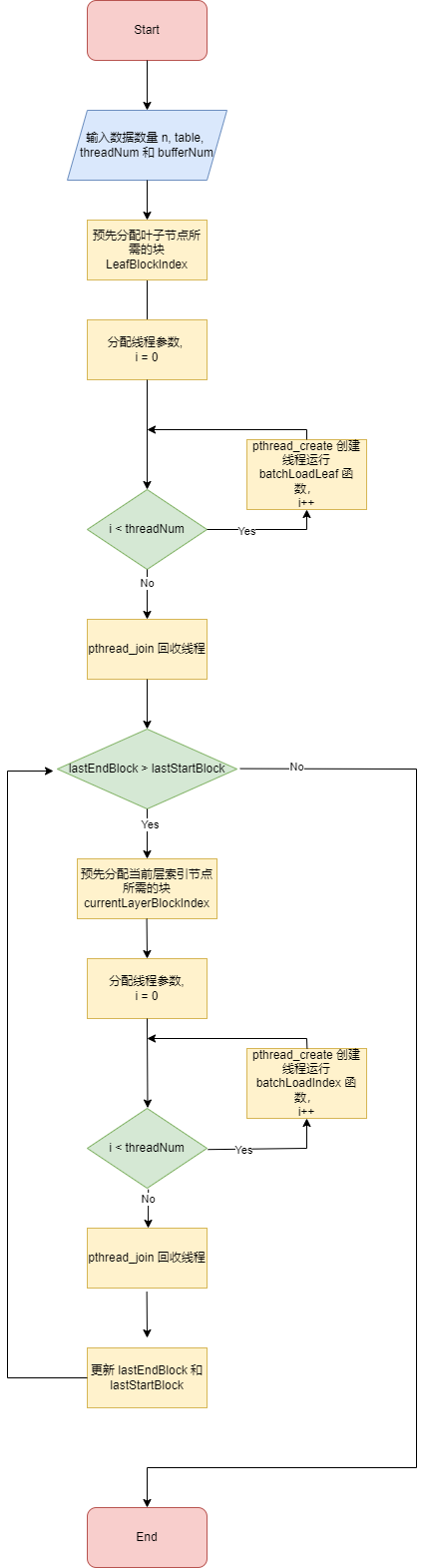
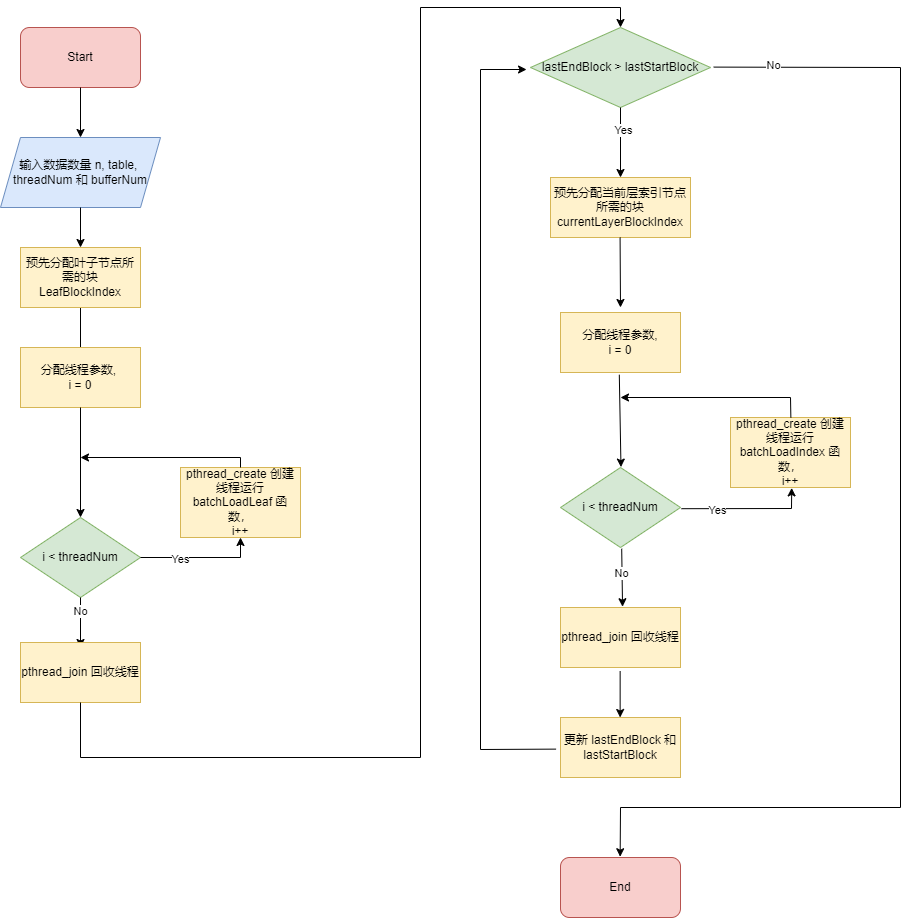
Ⅲ . 算法流程图
4.1 连续分配块
4.2 连续写磁盘
Ⅴ . 关键代码描述
5.2
Ⅵ . 实验结果分析
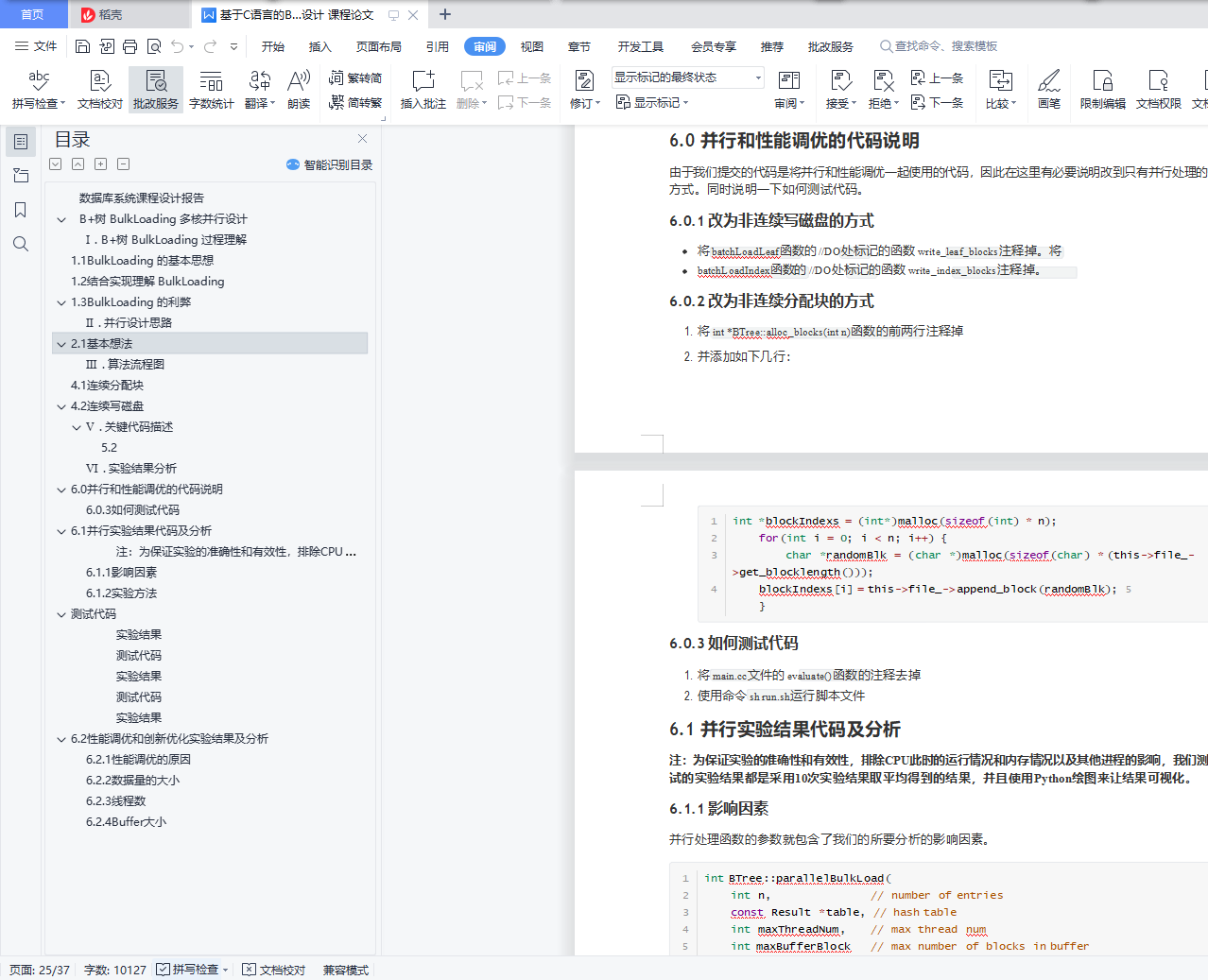
6.0 并行和性能调优的代码说明
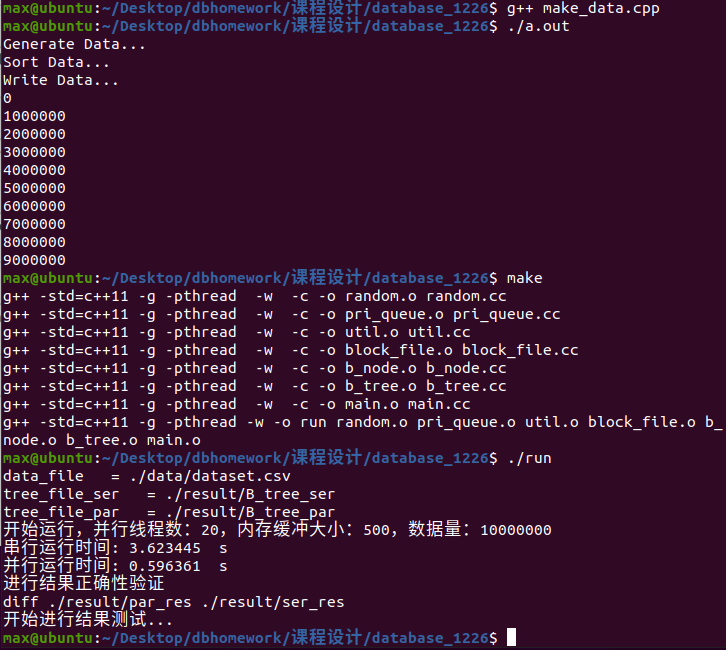
6.0.3 如何测试代码
6.1 并行实验结果代码及分析
6.1.1 影响因素
6.1.2 实验方法
测试代码
6.2 性能调优和创新优化实验结果及分析
6.2.1 性能调优的原因
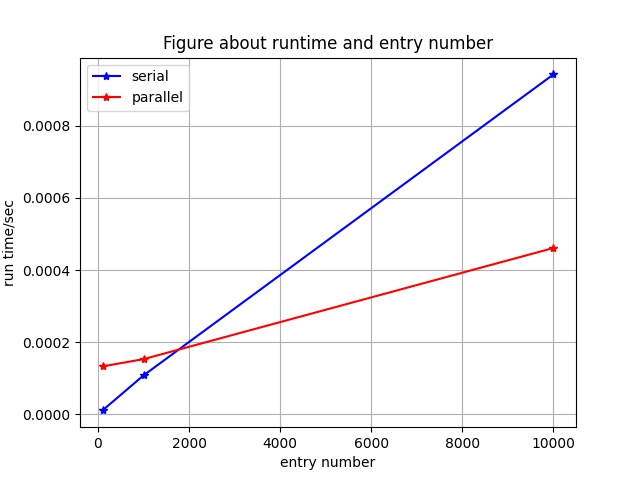
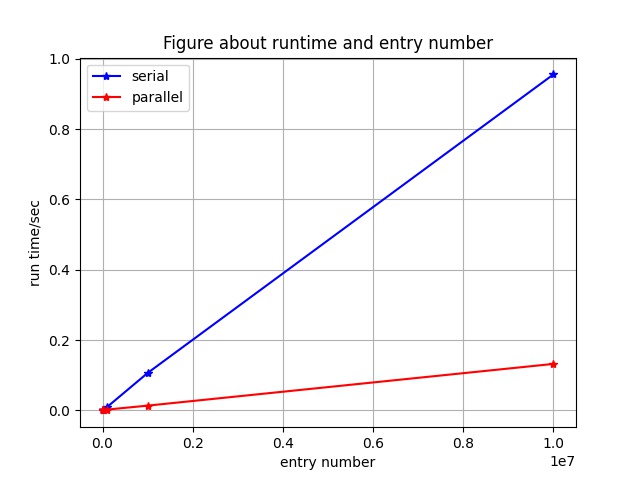
6.2.2 数据量的大小
6.2.3 线程数
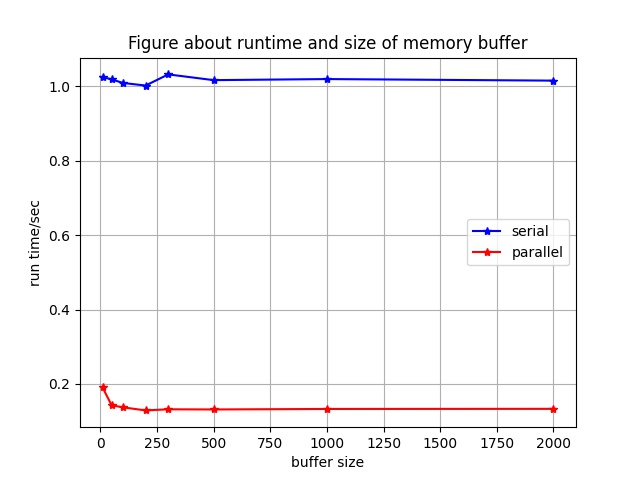
6.2.4 Buffer大小
Ⅰ . B+树 BulkLoading 过程理解
1.1 BulkLoading 的基本思想
在理解 BulkLoading 过程之前，要先理解 B+ 树的结构特性：首先，B+ 树只在叶子节点中保存数据，非叶子节点只保存索引，叶子结点的数据又根据关键字从小到大顺序排序。
我们单看叶子节点一层，就可以发现起始它和一个有序的数据数组在形状上是一致的。这意味着如 果我们的现有数据是有序排列的，我们就可以直接从小到大“铺”到叶子节点上。再加上B+树的子节点的 个数有限制，故我们可以直接估算出要多少个叶子节点，多少个相邻的叶子节点有一个共同的父索引节 点，把上述过程同样运用到索引节点上，我们就可以自底向上地构建出一棵完整的B+树。
得到一个BulkLoading过程的一个完整描述：先从底层叶子节点构建，从左往右按顺序构建一个双 向链表；从下往上，一层层构建索引节点，每一层也是从左往右构建索引节点。
1.2 结合实现理解 BulkLoading
讨论 BulkLoading 的实现细节：节点的结构、磁盘文件的数据对应 。
叶子节点：相邻节点之间有互相指向的指针，叶子层构成了一个双向链表。每个节点有两个数组， 一个储存Key，一个储存Value，一个Key对应有16个Value，这里的 Value 就是实际的数据，也就是数据项（Data Entry）。
索引节点：每一层的相邻的索引节点也存在双向指针，索引节点都是根据下一层的子节点生成的， 每个索引节点有两个数组，一个存储Key，一个存储指向子节点的指针，二者数量相等。一个键值
Key和一个指针就构成了一个索引项（Index Entry）。
与磁盘文件的关系：磁盘文件被划分为一个个块（Block），每一个节点就对应一个块，块通过块 号区分，表示节点存储到文件的区域编号。这样，索引项中所谓的指针，就可以用块号来表示。
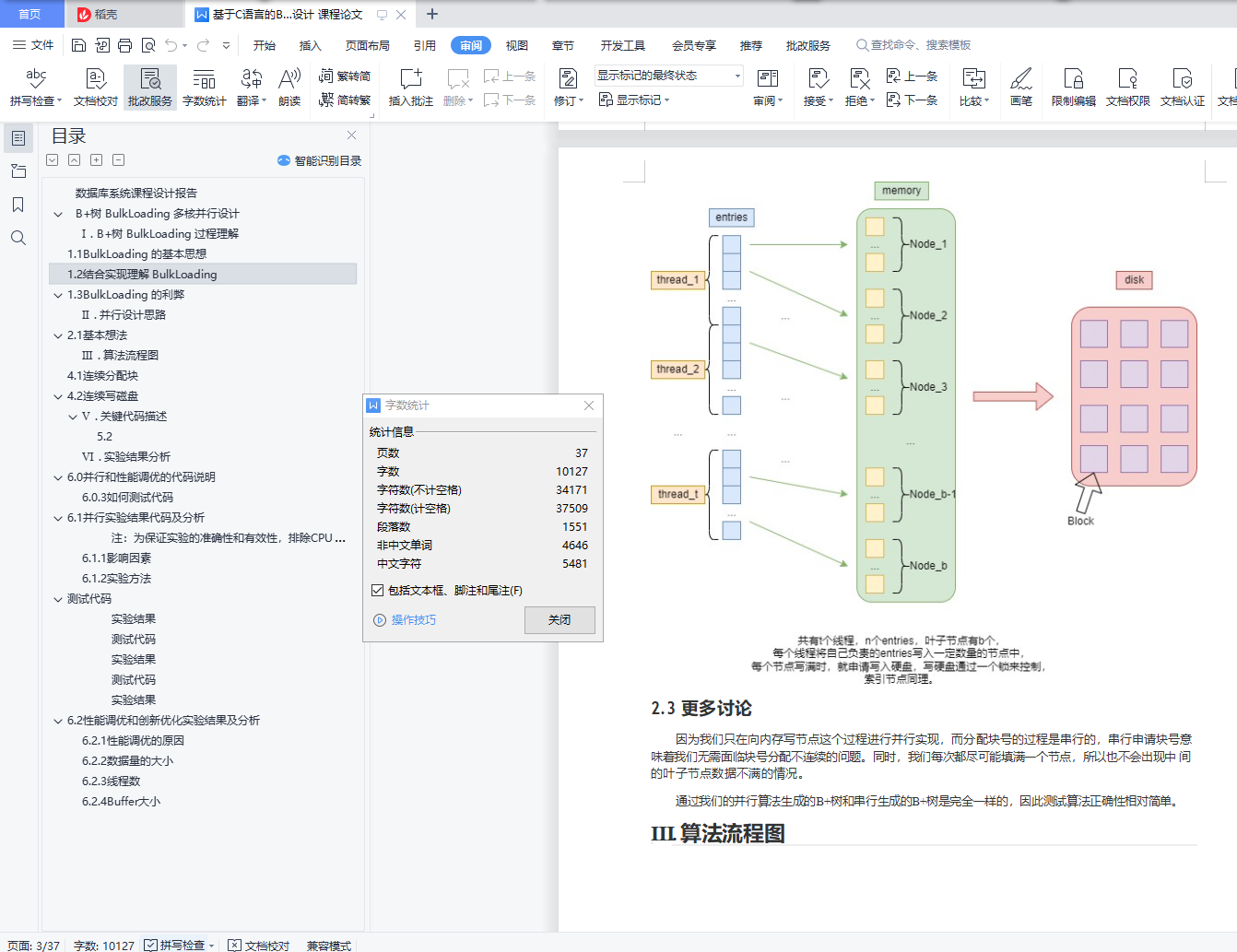
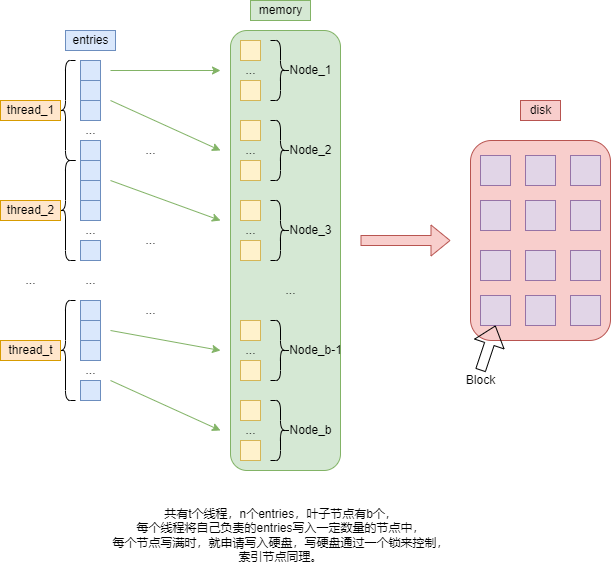
这样，BulkLoading 的过程就包含：在内存中组织叶子节点和索引节点，组织的方式就是创建与块一样大的缓冲区，将数据项、索引项拷贝进去，然后再写入到磁盘块里。（区分这些过程有利于并行实 现）
因为块号的分配是连续的，块的大小是固定的。在 BulkLoading 过程中，我们只需要记录下一层中第一个块号和最后一个块号，就可以直接算出上一层节点的所有子节点的块号，无需访问子节点。
在B+树中一个节点的索引值可以设置为第一个项的键值，因为 BulkLoading 是自底向上的构造过程，节点的索引值可以直接给出，且过程中不会改变，不需要B+树插入删除节点时的那样进行动态调 整。在设计上采用 On-the-fly 的策略，在一层一层循环构建的过程中，线程函数每次都保存一层的键值并返回，键值数组再用于构建上一层节点，无需进行IO访问。
1.3 BulkLoading 的利弊
相比于通过插入节点构造B+树，BulkLoding充分利用了数据有序的特性，让每一个节点构造过程的 复杂度都为O(1)，构造过程中不存在节点的分叉、合并等调整，生成B+树的过程非常快。
通过BulkLoading构造B+树也可能存在潜在的问题：因为每一个节点从左到右都是尽可能填满的， 当需要插入新节点时，B+树结构的变动可能会非常大，会产生较大的时间开销。
或许我们可以加入一个填充因子来控制BulkLoading每次为一个叶子节点填出的数据项的个数，让 叶子节点的数据项不是满的，这样可以减弱插入节点对B+树结构造成的影响。
