实现并对比线性分类器与非线性分类器

一、分类器简述

1.1 线性分类器

1.2 Softmax函数和交叉熵损失

1.3 随机梯度下降

1.4 梯度推导

1.5 基于基函数的非线性分类器

1.6 过拟合与正则化二、分类器实现

2.1 线性分类器

2.2 非线性分类器三、数据集描述

3.1 Dry Bean 数据集

3.2 葡萄酒数据集

3.3 肥胖症数据集

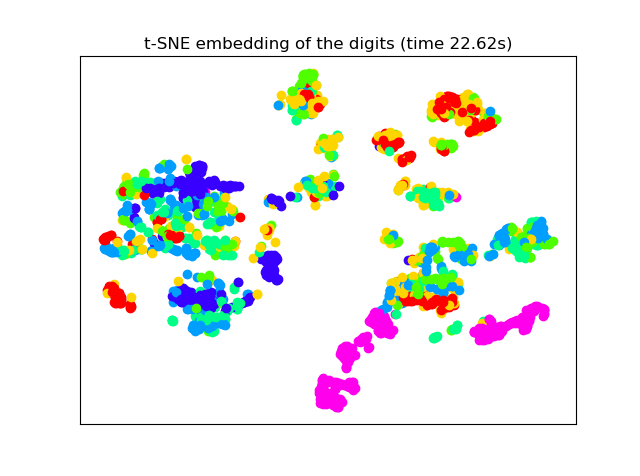
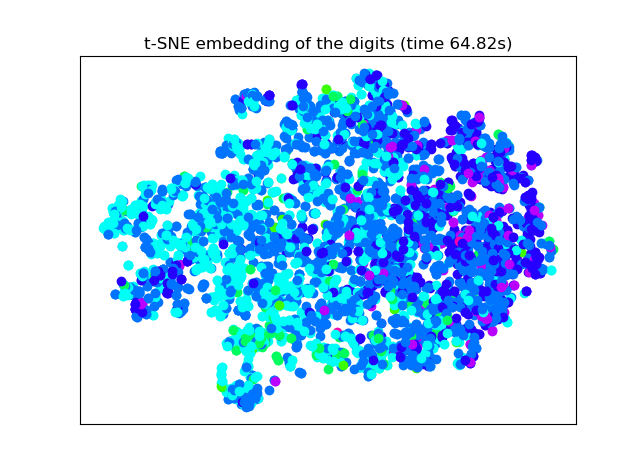
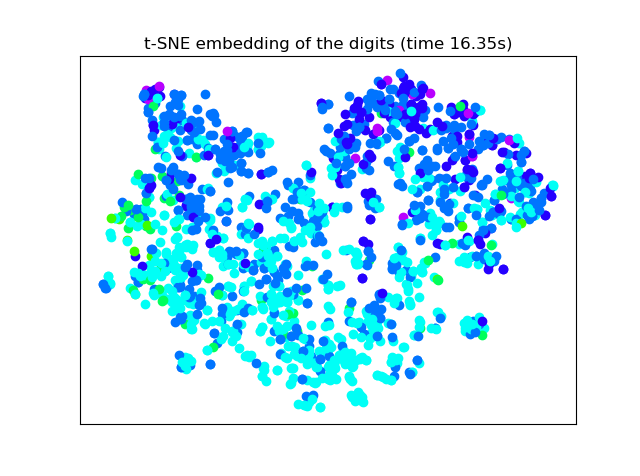
3.4 数据降维可视化四、实验结果分析

4.1 交叉验证学习率

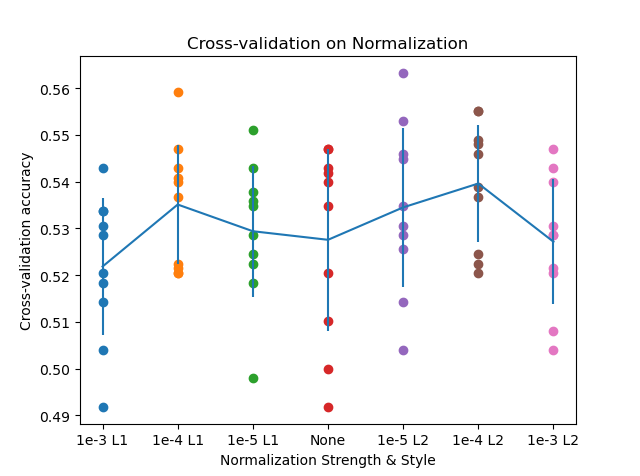
4.1 交叉验证正则化系数

4.3 分类器交叉验证

4.4 权重可视化与损失函数变化

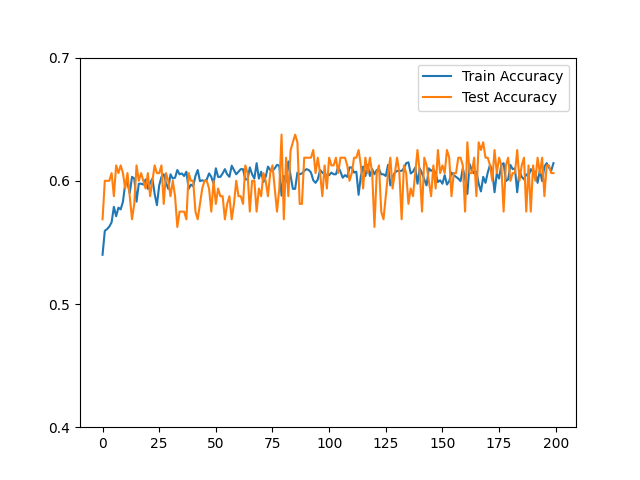
4.5 正确率测试

4.6 精准度和召回率测试五、结论

一、分类器简述

分类器将原始数据映射到类别分数的函数（Score Function）上，然后通过损失函数（Loss Function）量化预测分数和真实值标签的差异，再将此转换为一个最小化损失函数的优化问题。

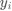
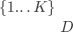
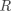我们假设每一个原始训练数据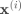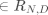都有对应标签，一个原始数据是数据集

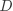
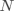
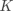上的一个有的向量，标签用一个整数表示，时数据样本的个数，是一个样本的维度，是类别的总数。

首先定义关于分数的函数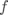，该函数将原始数据映射到每个类的置信度分数上。对于线性分类器

（Linear Classifier），这个函数可以表示为：

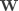
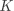
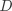
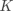
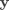
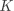
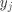
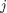其中是一个的权重矩阵（Weights），是一个的偏移向量（Bias Vector），计算结果同样是一个的向量，表示

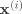对应类别的分数。

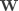
线性分类器的训练过程就是通过训练集出一个和，测试过程就是测试集使用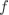

来得到一个分类分数，再经过一些处理（例如 Softmax）来选出预测的标签。

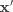
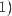
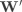在实现时，做一个矩阵乘法后添加一个偏置向量相当于给所有输入向量添加一个常数为1的偏置维数，得到，它是一个

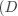的向量，并将权矩阵扩展一个偏置列得到新矩阵，其大小为

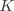
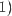
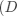。因此，在实现时我们可以通过在所有向量上附加一个值为1的维度，就可以只学习一个矩阵，而不是权重矩阵和偏移向量。