目录
一、 实验目的及要求 0
二、 算法原理概述 0
三、 软件开发环境及工具 0
四、 实验内容 0
五、实验总结 0
六、参考文献 0
附录 完整源代码 0
一、实验目的及要求 1
二、算法原理概述 1
（一）Huffman树 1
1.Huffman树简介 1
2.Huffman树的构造 2
（二）Huffman编码 2
1.Huffman编码简介（来源于百度百科） 2
2.Huffman编码的实现 3
（三）Huffman译码 3
1.Huffman译码简介 3
2.Huffman译码的实现 4
（四）huf文件编码算法 4
1.对二进制文件的写入 4
2.Huffman编码的实现 4
char bit_number_transform(int n[]) { 5
（五）huf文件译码算法 5
1.对二进制文件的读取 5
2.对Huffman编码的解压缩 5
三、软件开发环境及工具 6
四、实验内容 6
五、实验总结 16
六、参考文献： 17
一、实验目的及要求
（1）考查二叉树存储表示及其基本操作实现。
（2）赫夫曼树的建立。
（3）赫夫曼树编码和译码算法。
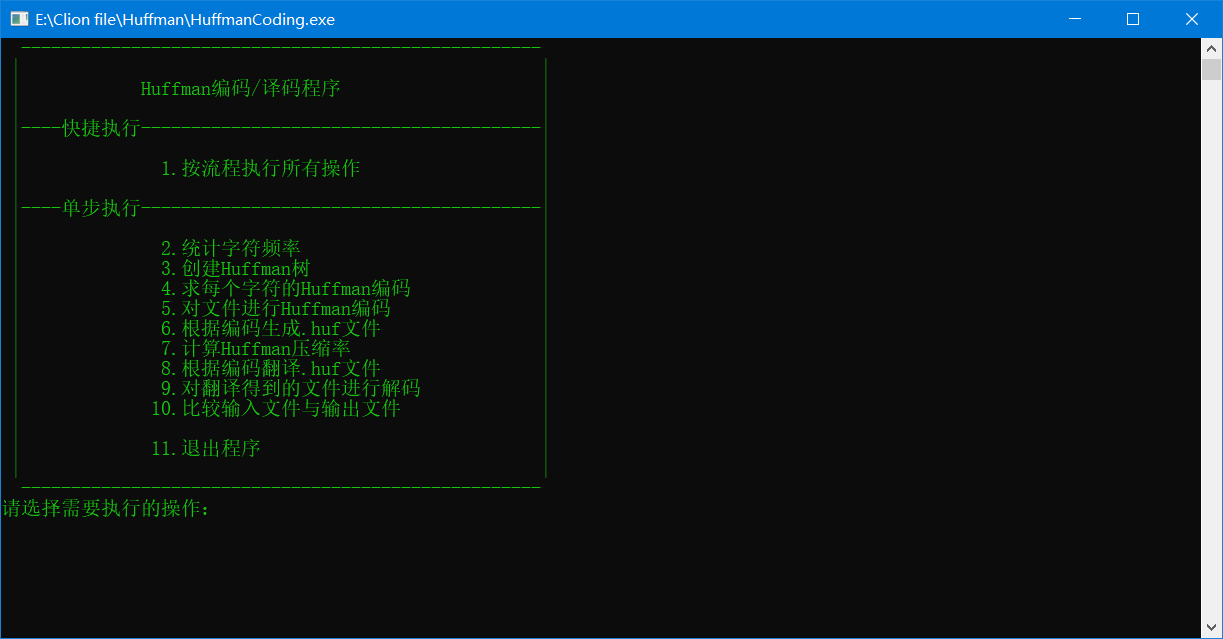
（4）系统功能：从文件或键盘读入一串电文字符，实现赫夫曼编码和译码。
（5）密码文件以文件的形式进行存放。
二、算法原理概述
（一）Huffman树
1.Huffman树简介
（1）基本概念
路径：树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。
路径长度：路径上的分支数目称作路径长度。
树的路径长度：从树根到每一个结点的路径长度之和。
结点的带权路径长度：在一棵树中，如果其结点上附带有一个权值，通常把该结点的路径长度与该结点上的权值的乘机称为节点的带权路径长度。
树的带权路径长度：树中所有叶子结点的带权路径长度之和，通常记作
WPL=
（2）Huffman树的概念
假设有n个权值{w1，w2，…，wn}，试构造一颗有n个叶子结点的二叉树，每个叶子结点带权为wi，则其中带权路径长度WPL最小的二叉树称做最优二叉树或Huffman树。
Huffman树是一类带权路径最短的树，又称最优二叉树。
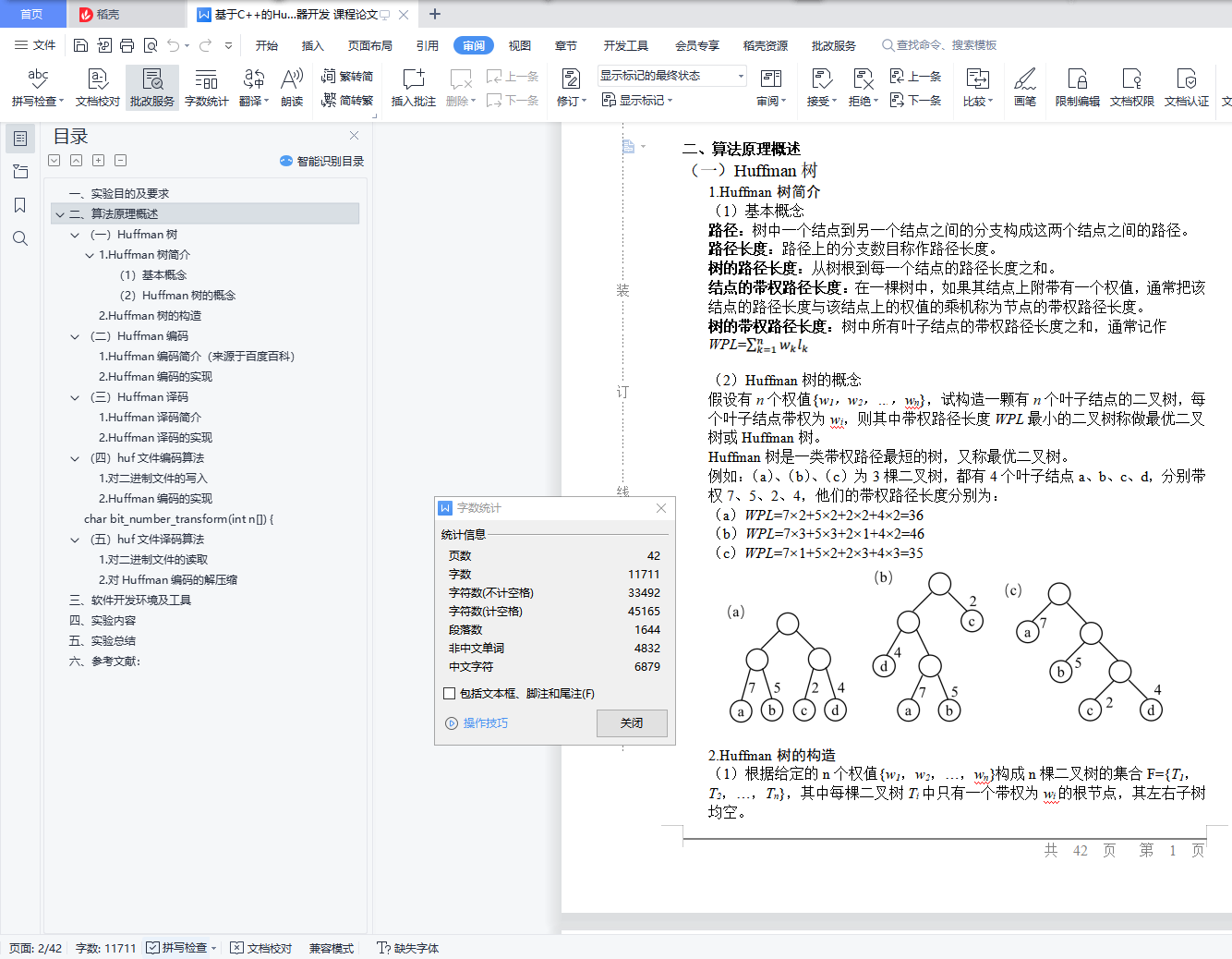
例如：（a）、（b）、（c）为3棵二叉树，都有4个叶子结点a、b、c、d，分别带权7、5、2、4，他们的带权路径长度分别为：
（a）WPL=7×2+5×2+2×2+4×2=36
（b）WPL=7×3+5×3+2×1+4×2=46
（c）WPL=7×1+5×2+2×3+4×3=35