目录
一、需求分析 2
二、逼近法 2
1、算法原理 2
2、误差分析 3
三、常微分方程 4
1、算法原理 4
2、误差分析 5
四、cordic 算法 7
1、算法原理 7
2、误差分析 8
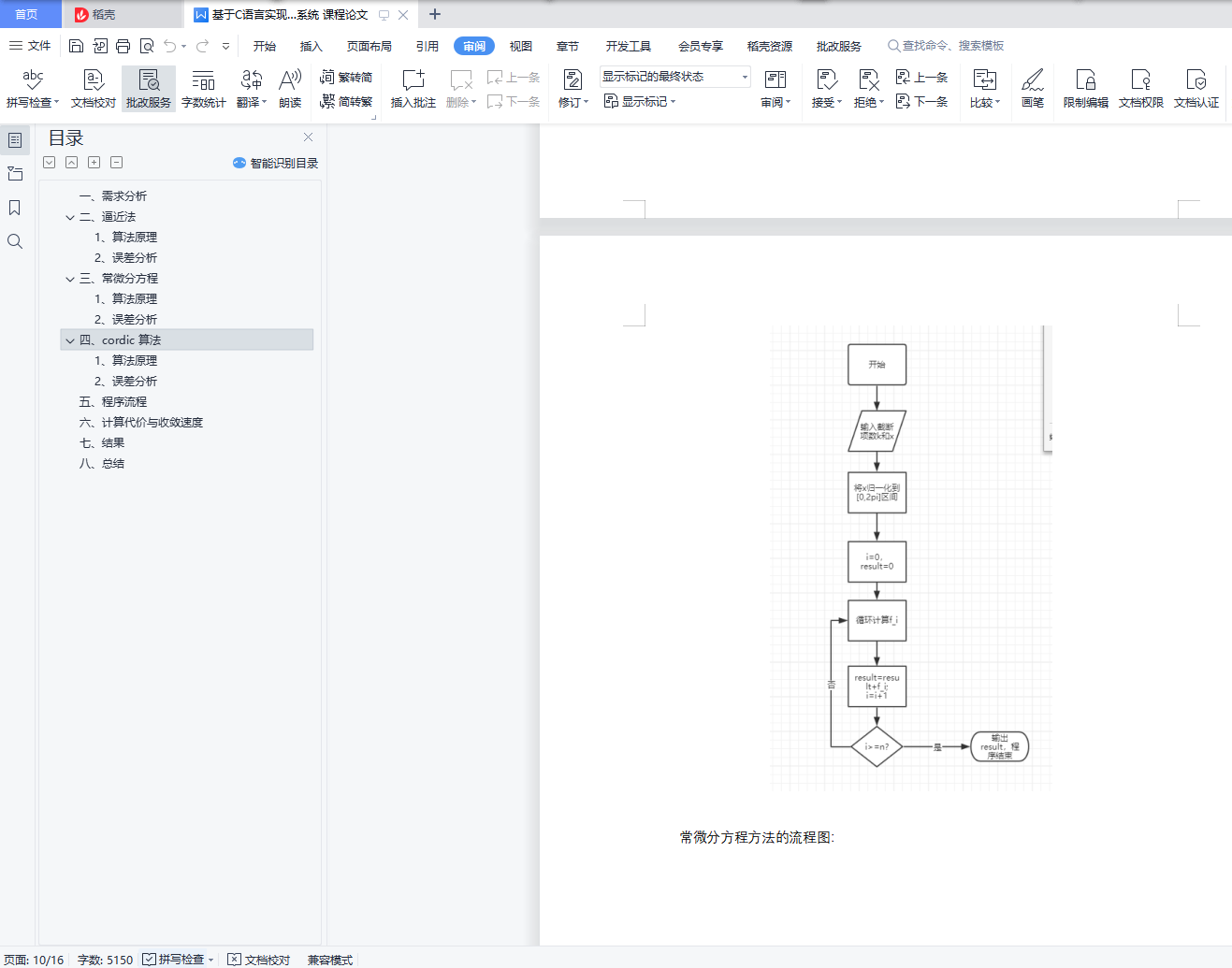
五、程序流程 9
六、计算代价与收敛速度 12
七、结果 14
八、总结 15
一、需求分析
本次大作业需要求解 sin(x),x 的取值范围是任意的,需要保证算法能精确到小数点后 4 位,需要对运算结果进行误差分析,包括方法误差和舍入误差。根据分析得到误差确定迭代次数等。
通过完成这次大作业,我提高了运用理论知识解决实际问题的能力,比如改进欧拉法、方程根的数值解等;同时也学到了很多新知识,比如 cordic 算法。
这次大作业的难点在与误差分析,在对实际问题的结果进行误差分析的过程中, 我加深了对方法误差和舍入误差的理解,认识到了实际问题中误差分析的必要性。
将一个数值算法投入应用中,除了要考虑它的误差,另一个重要因素是算法的复杂度,cordic 算法的实现虽然需要提前准备一些数据,但其运算速度很快,这也是它被广泛应用的原因。
此外,我为我的程序设计了简单的用户界面,感觉程序的实用性更强了。
总之,通过这次大作业我增长了很多新知识,加深了对理论知识的理解,也加强了我动手解决实际问题的能力。