目录
1求解多极小函数 2
1.1SA 算法 2
1.1.1算法流程 2
1.1.220 次随机实验的统计结果 3
1.1.3目标函数的变化曲线 3
1.2GA 算法 6
1.2.1编码 6
1.2.2算法流程 6
1.2.3算法参数 7
1.2.420 次随机实验的统计结果 7
1.2.5目标函数的变化曲线 7
2TSP 问题 8
2.1SA 算法 8
2.1.1算法流程 8
2.1.220 次随机实验的统计结果 8
2.2GA 算法 13
2.2.1 编码 13
2.2.2算法流程 13
2.2.3算法参数 13
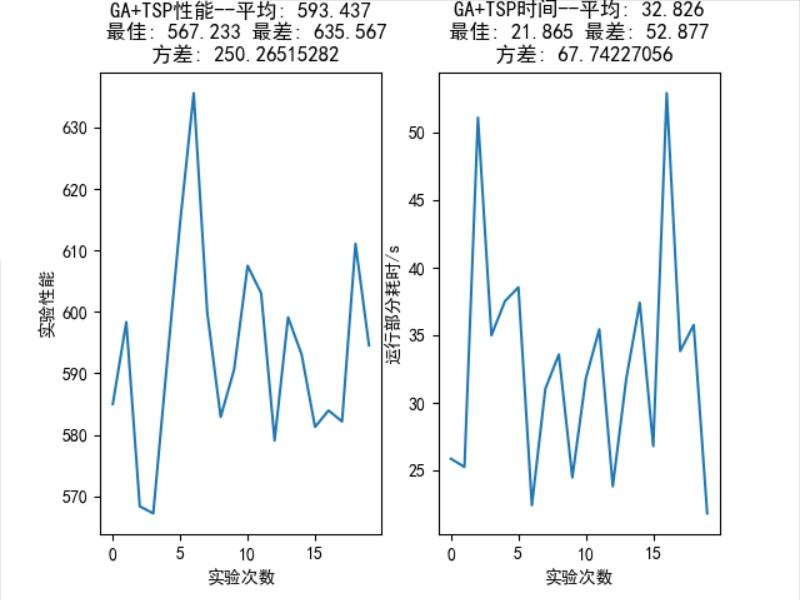
2.2.420 次随机实验的统计结果 13
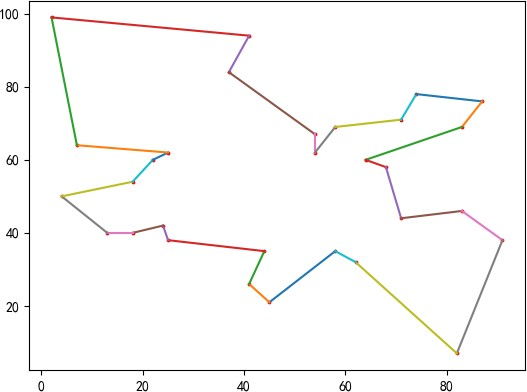
2.2.5一次实验结果 13
3算法特点 17
3.1 SA 17
3.2 GA 17
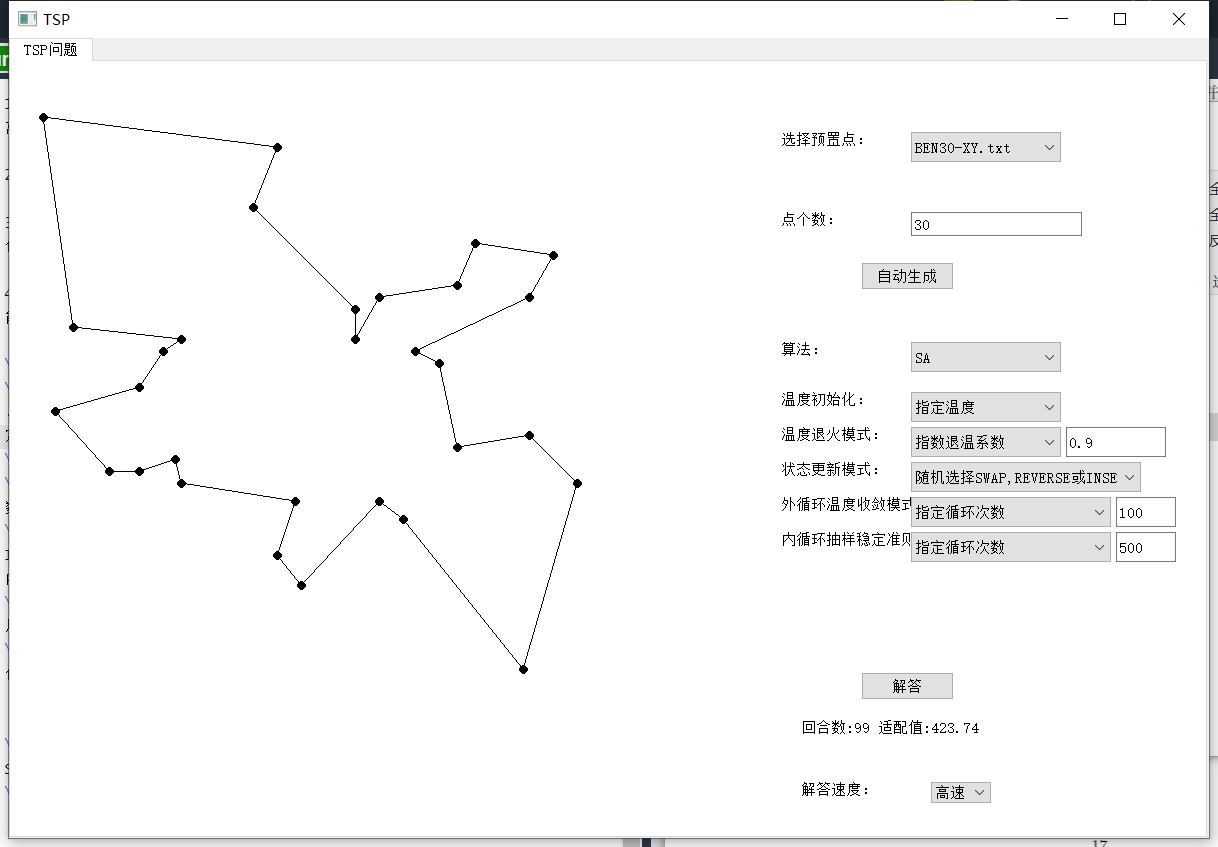
4TSP 可视化应用程序 17
5实验分工 18
1求解多极小函数
求解多极值函数问题中，我们需要求出函数的最值，我们以函数 f (x0, x1) = −x1 ∗ sin(x0) −
x0 ∗ cos(x1) 为例，求它在 x0, x1 ∈ [−10, 10] 区间内的最小值。
使用 MATLAB 画出的函数图像如图1所示，其最小值可用 matlab 库函数求出，约为-17.394， 同时该函数有多个局部极小值。

算法流程与上文基本类似，不同之处在于：
步骤 1 中，初始温度可以有两种生成方式：按照经验设定固定初温要更大，随机选择指定数量计算方差时指定的元素数目也大得多；初始解在离散的 TSP 问题中为旅行商所经城市的路线。
步骤 4 为状态更新，在 TSP 问题中，可以通过进行两位置元素交换、两位置之间的元素逆序、把指定某一段序列插到第三个位置之后或者把上述操作按照概率混合的方法产生新的状态，  即新的旅行商路线。