机器人路径规划的时间高效A*算法
作者:Akshay Kumar Guruji, Himansh Agarwal, D. K. Parsediya*
Madhav Institute of Science & Technology, Race course road, Gwalior, Madhya Pradesh, India
摘要
当今时代的焦点主要集中于现代化、工业化和自动化的发展。其中,人的任务逐渐被机器人取代,以达到高精度,高效率,快速和多样性。例如在工业生产的过程中,这些机器人被用来在工作场所携带重物。但由于环境或者工作区域可能是动态变化的,必须要确保设计的寻路算法或规则能够提供最优的无碰撞路径。A*算法是一种基于启发式函数的路径规划算法。为了找到零碰撞概率的最佳解决方案,它需要对工作区域内的每个节点进行启发式函数值的计算,并且涉及到太多相邻节点的检查。因此,它需要大量的处理时间而降低了工作速度。本篇论文提出了用于减少处理时间的A*算法的改进。被提议的A*算法确定启发式函数的值就在碰撞阶段之前而不是最初阶段,它明显减少了处理时间,带来了更快的速度。本文应用了从初始点到目标点的MATLAB仿真机器人运动。提出的改进版A*算法在应用于一些案例时能够在处理时间上表现出最大95%的减少量。
关键词:路径规划,最优路径,启发式函数,处理时间和路径长度
第1章 简介
路径规划是找到空间中从一点到另一点的最优路径的方法。它通过确定源点和目标点之间的最短路程,来优化他们之间的路径【1-2】。它有时也被称为运动规划,因为它有助于决定在工作环境中的任何物体的运动。一个物体可以看作是一个在本质上是自主的机器人,因为它可以使用路径搜索算法来决定自己在空间中移动所要经过的点,这种机器人被称为移动机器人【3】。路径规划也被定义为将期望的运动分解为若干迭代的步骤来分离运动以优化一些实体对象的过程。
环境因素在路径规划问题中扮演着十分重要的角色。基于工作场所的性质,路径规划可以分为离线规划和在线规划两种类型。在离线路径规划中,工作空间对应的数据里所包含的障碍物是固定不变的,在使用寻路算法计算出最优路径之前,已知的障碍物的几何形状是给定的【4】。但是对于在线路径规划,很多作者和发表的文章都表明:机器人需要使用传感器或者实时数据采集设备来获取整个工作空间中不断发生移动的障碍物的位置【5-8】。但是,在线路径规划这种想法的实现需要非常复杂的建模过程。在本篇论文中应用的条件是用来处理静态环境因素的,所以所设计的算法在本质上属于离线路径规划。各种各样的路径规划算法比如遗传算法、神经网络算法和A*算法等都被应用于移动机器人导航中【9】。它将整个的工作空间看作是一个导航网格,移动机器人通过找到覆盖最少导航网格数量的路径来达到目的地。A*算法使用启发式函数,通过计算整个工作空间内所有节点的函数值来得到最佳的解决方案【10】。当然,A*算法也有一定的局限性,因此在本研究之前已经有很多人提出了A*算法的改进版【11-13】。
A*算法是一种计算机算法,为了连续不断得检测各节点,它必须需要配备高配置的处理器。如果从源点到目标点之间的距离很大,那么从源点到目标点的A*算法实现过程将会涉及太多的相邻节点的检测,从而大大增加了处理时间【14】。在这种情况下,低配置的处理器需要更多的时间来规划路径,本篇论文接下来提出的改进版算法已经很好地解决了以上问题。本项研究工作设计了一个减少处理时间的改进版A*算法。该算法并不需要计算工作空间中所有节点的启发式函数值,它只是在碰撞阶段和频繁地处理过程之前测量函数值,对于那些还在使用的低配置的老旧处理器的工作场景该算法一样可以被应用。当然该算法关注的重点也不能失去传统A*算法的优点。当源点和目标点之间的距离足够大时,被命名为时间高效A*算法的该改进版A*算法可以在执行时间上带来75%的锐减。
本篇论文一共包含四个部分。第一部分是路径规划算法的简介;第二部分是对本文提出的时间高效A*算法的详细阐述,包括算法执行需要的条件及流程图等;第三部分图解了模拟寻路的过程,并分析了比较研究得出的结果;第四部分给出了全文的结论。
第2章 提出的算法与其执行条件
传统的A*算法需要花费大量的时间来遍历所有节点,计算每个节点对应的启发式函数值。本文提出的时间高效A*算法会遍历所有节点,但是只在碰撞阶段之前计算每个节点的启发式函数值。这将大大减少处理时间,使移动机器人可以迅速地完成它的工作。图一为本文提出的时间高效A*算法的流程图。本文将该算法应用于MATLAB仿真中来估算处理时间。
2.1 输入阶段
首先,把机器人工作空间所对应的图片转化为二进制图像,其中的黑色区域表示工作空间中的障碍物。然后将图片对称地放到二维平面X, Y的原点,给出源点坐标和目标点坐标作为输入。
2.2 接近检测阶段
这个阶段涉及到检测源点和目标点之间的距离,如果这个距离很小,那么意味着满足接近条件然后算法进入A*阶段,否则继续进行下一步。
2.3 确定斜率和投影像素阶段
计算穿过源点和目标点的线的斜率作为它的终点,那么像素将会沿着源点到目标点之间的虚线从源点投射到图像上。检测源点和目标的坐标距离是否满足临界条件来判断改进的A*算法是否适用于这些坐标点的集合。如果源点和目标点两者之间的距离很近,那么使用原始的A*算法将会更合适,但如果距离很远,并且两者之间有障碍物,那么改进版的A*算法将会更合适。如果斜率不统一,那么像素将会根据H值和G值被投影在任意计算出的斜率上。
2.4 碰撞阶段
如果像素的投影经过目标点,那么可以得到一条经过源点和目标点的直线。如果像素的投影命中了障碍物,计算碰撞前点的坐标,将它称之为转换点(缩写为S点),同时在得到S点之后,算法进入A*阶段。
2.5 A*或转换阶段
将S点作为源点,将终点作为目标点,使用A*算法获得两点之间的最短路径。这个过程被称为转换阶段,因为该算法现在使用预定的A*算法做路径规划。将从源点到切换点S之间的直线路径和从切换点S到目标点之间的A*寻路结果结合到一起就是时间高效A*算法得到的最终路径。然后从步骤10获得的路径被馈送到机器人以从源到目的地移动。
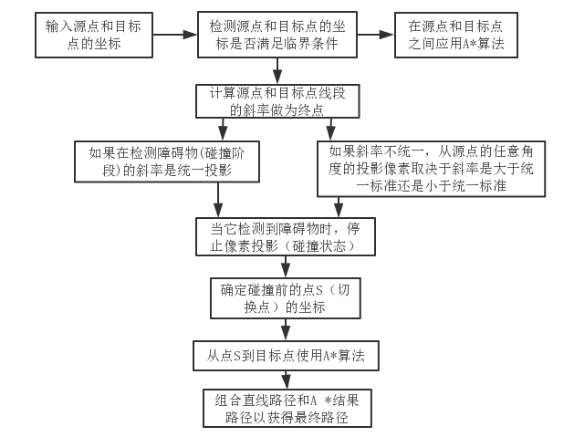
图2�1 提出的A*算法流程图
当满足某些条件时,上述方法得出问题的最优解。问题的工作环境被认为是静态的,机器人的位置是已知的。在应用所提出的算法之前,源点、目标点和机器人的坐标或相对位置是已知的。
第3章 仿真和结果
所提出的算法在MATLAB版本7.12.0.635(R2011a)上实现,其中使用各种图形功能。由顶置摄像头拍摄的竞技场的图像(如前一节所述)被转换为二进制形式或位图图像。处理时间和路径长度可以作为MATLAB程序的输出来获得。而且在英特尔奔腾CPU B9600 @ 2.20GHz上测试完整的代码,表明算法在慢速处理器上的可靠性。
表格 3�1案例和参数
|
序号
|
案例编号
|
机器人的初始位置(源点坐标)
|
机器人的重点位置
(目标点坐标)
|
|
1
|
1
|
源点 =(5,5)
|
目标点 =(90,90)
|
|
2
|
2
|
源点 =(5,5)
|
目标点 =(70,20)
|
|
3
|
3
|
源点 =(5,5)
|
目标点 =(40,80)
|
|
4
|
4
|
源点 =(5,5)
|
目标点 =(70,70)
|
|
5
|
5
|
源点 =(5,5)
|
目标点 =(35,90)
|
|
6
|
6
|
源点 =(5,5)
|
目标点 =(50,50)
|
表3-1说明了应用于仿真模拟的不同环境情况,机器人从被命名为源点的初始位置开始它的遍历,然后到达被称为目标点的目的地。表格中列出了源点和目标点的坐标,并且所有用例的源点位置都是固定的。
图3-1阐述了将表一中的参数集应用于传统A*算法的仿真模拟结果。图3-2阐述了将相同的参数集应用于本文所提出的时间高效A*算法的仿真模拟结果。两张图都显示了从源点到目标点的遍历路径,并且在其旁边记录了处理的时间和路径的长度。本文的研究由几个案例的仿真模拟结果构成,它们可以证明本文提出的时间高效A*算法的时间效率。
|
传统A*算法仿真
|
|
 CASE1 CASE1
|
处理时间:
6.881205c+001
路径长度:
6.976955c+002
|
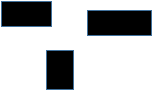 CASE4 CASE4
|
处理时间:
4.360535c+001
路径长度:
5.123402c+002
|
|
 CASE2 CASE2
|
处理时间:
2.388457c+001
路径长度:
3.767767c+002
|
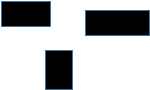 CASE5 CASE5
|
处理时间:
5.088388c+001
路径长度:
4.871320c+002
|
|
 CASE3 CASE3
|
处理时间:
2.661417c+001
路径长度:
4.592031c+002
|
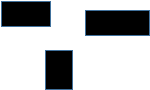 CASE6 CASE6
|
处理时间:
2.099893c+001
路径长度:
3.474874c+002
|
图3�1传统A*算法的仿真结果
|
本文提出的时间高效A*算法仿真
|
|
 CASE1 CASE1
|
处理时间:
3.610599c+001
路径长度:
6.838391c+002
|
 CASE4 CASE4
|
处理时间:
2.274836c+001
路径长度:
5.123402c+002
|
|
 CASE2 CASE2
|
处理时间:
7.462159c+000
路径长度:
4.466063c+002
|
 CASE5 CASE5
|
处理时间:
4.916487c+001
路径长度:
4.871320c+002
|
|
 CASE3 CASE3
|
处理时间:
7.462159c+000
路径长度:
4.466063c+002
|
 CASE6 CASE6
|
处理时间:
7.036298c+000
路径长度:
3.474874c+002
|
图3�2本文提出的时间高效A*算法的仿真结果
表3-2记录了来自仿真模拟的观察结果,然后将本文提出的时间高效A*算法的仿真模拟结果与传统A*算法进行比较,并记录处理时间和路径长度的百分比变化值。最终的观察结果如下所述:
l 对于大多数情况而言,虽然路径长度有了微小幅度的增长,但是处理的时间却有了很大幅度的减少。这对于处理缓慢的处理器是非常有益的。本文所提出的时间高效A*算法所花费的时间比传统A*算法所花费的时间一半还少,这足以弥补路径长度的微小增长。
l 在一些情况下,使用本文所提出的的时间高效A*算法,可以发现在处理时间和路径长度上都比较少,从而能够提供比传统A*算法更加合适的路径。
l 有些时候,针对本文提出的时间高效A*算法计算出的处理时间比相同路径长度的传统A*算法要少,因此它是更加合适的解决方案。
表格 3�2 仿真结果及其比较
|
序号
|
传统A*算法
|
本文提出的算法
|
比较
|
|
处理时间
|
路径长度
|
处理时间
|
路径长度
|
处理时间减少的百分比
|
路径长度增大的百分比
|
|
1
|
6.881205e+001
|
6.976955e+002
|
3.610599e+001
|
6.838391e+002
|
47.54%
|
1.98%
|
|
2
|
2.388457e+001
|
3.767767e+002
|
1.280379e+000
|
3.914363e+002
|
94.6%
|
3.89%
|
|
3
|
2.661417e+001
|
4.592031e+002
|
7.462159e+000
|
4.466063e+002
|
71.96%
|
2.74%
|
|
4
|
4.360535e+001
|
5.123402e+002
|
2.274836e+001
|
5.123402e+002
|
47.83%
|
0%
|
|
5
|
5.088388e+001
|
4.871320e+002
|
4.916487e+001
|
4.871320e+002
|
3.38%
|
0%
|
|
6
|
2.099893e+001
|
3.474874e+002
|
7.036298e+000
|
3.474874e+002
|
66.43%
|
0%
|
第4章 结论
在本研究工作中已经完成了对传统A*算法和本文提出的时间高效A*算法的MATLAB编程及仿真模拟,展示了两种算法在路径搜索时采用的方法之间的计较。对于这两种算法,本文都计算并观察了处理时间的百分比减少量和路径长度的百分比增加量。在本文中,证明了改进的时间高效A *算法将处理时间至少降低了65%,虽然伴随着路径长度最大增加了3.4%。当源点坐标和第一个障碍物坐标的距离大于直线路径的长度时,改进的时间高效A*算法要优于传统的A*算法,并且还减少了将启发式函数(比如传统A*算法)应用于每个相邻节点之间的检测次数。因此,可以得出结论:改进的时间高效A*算法虽然有路径长度上的一点小成本,但处理时间的减少要大大优于传统的A*算法,并且可以完美地适用于需要快速处理的应用程序。
引用
[1] S. A. Hutchinson, R. L. Cromwell, and A. C. Kak: Planning Sensing Strategies in a Robot York Cell with Multi-Sensor Capabilities IEEE
Trans on Robotics and Automation 1988 IEEE.
[2] Alexopoulos, C.: path planning for mobile robots Systems, Man and Cybernetics, IEEE Transactions on (Volume:22 , Issue: 2 )
[3] Janusz Pochmara, Wojciech Grygiel, Radosław Koppa, Krzysztof Kamiński “Mobile Robot Platform for Real-Time Search Algorithms” ;
International Conference "Mixed Design of Integrated Circuits and Systems" , June 20-22, 2013, Gdynia, Poland
[4] Ismail, AL-Taharwa, Alaa Sheta, and Mohammed Al-Weshah. "A mobile robot path planning using genetic algorithm in static
environment." Journal of Computer Science 4.4 (2008): 341-344.
[5] Seungho Lee' and Teresa M. Adamsb : A PATH PLANNING ALGORITHM FOR AUTOMATED CONSTRUCTION EQUIPMENT
,automation and Robotics in Construction XVI 1999 by .CC3M.
[6] Beom, H.R. , Koh, K.C. ; Cho, H.S.: Behavioral control in mobile robot navigation using fuzzy decision making approach Intelligent
Robots and Systems '94.
[7] Yasuda, G.; Takai, H., "Sensor-based path planning and intelligent steering control of nonholonomic mobile robots," Industrial Electronics
Society, 2001. IECON '01. The 27th Annual Conference of the IEEE ,
[8] Woong-Gie Han; Seung-Min Baek; Tae-Yong Kuc, "GA based online path planning of mobile robots playing soccer games," Circuits and
Systems, 1997. Proceedings of the 40th Midwest Symposium on , vol.1,
[9] R. Kala, A. Shukla, R. Tiwari, S. Roongta, R. R. Janghel (2009) Mobile Robot Navigation Control in Moving Obstacle Environment using
Genetic Algorithm, Artificial Neural Networks and A* Algorithm, Proceedings of the IEEE World Congress on Computer Science and
Information Engineering, Los Angeles/Anaheim, USA, pp 705-713.
[10] DaveFerguson, MaximLikhachev, and Anthony Stentz “A Guide to Heuristic based Path Planning”
[11] WANG Zhu, LIU Li, LONG Teng, YU Chenglong, KOU Jiaxun “Enhanced Sparse A* Search for UAV Path Planning Using Dubins Path
Estimation”; Proceedings of the 33rd Chinese Control Conference July 28-30, 2014, Nanjing, China
[12] Liping Cheng and Chuanxi Liu, Bo Yan “Improved Hierarchical A-star Algorithm for Optimal Parking Path Planning of the Large Parking
Lot”; Proceeding of the IEEE International Conference on Information and Automation Hailar, China, July 2014
[13] Elisabete Fernandes, Pedro Costa, Jos´e Lima, Germano Veiga “Towards an Orientation Enhanced Astar Algorithm for Robotic
Navigation”; 2015 IEEE
[14] Zhou Weiteng, Han Baoming , Li Dewei, Zheng Bin “Improved Reversely A star Path Search Algorithm based on the Comparison in
Valuation of Shared Neighbor Nodes”; 2013 Fourth International Conference on Intelligent Control and Information Processing (ICICIP)
June 9 – 11, 2013, Beijing, China



