目录
数独游戏 1
需求分析 1
解题思路 2
生成数独 2
1. 每行单元格包含整数1到9,且每个数恰好出现一次。 2
2. 每列单元格包含整数1到9,且每个数恰好出现一次。 2
3. 每个3×3的宫包含整数1到9,且每个数恰好出现一次。 2
1. 暴力搜索+回溯 2
2. 矩阵变换法 2
3. 全排列平移+行变换 2
求解数独 3
项目环境 3
项目文件结构 4
代码设计 5
命令行版的数独项目 5
关键函数流程图 9
一行代码将数独保存到txt文件 15
numpy之savetxt 15
random.sample之数独挖空 16
random之sample 16
main函数 17
GenerateEndgames类(生成终局) 19
Sudoku类(求解数独) 24
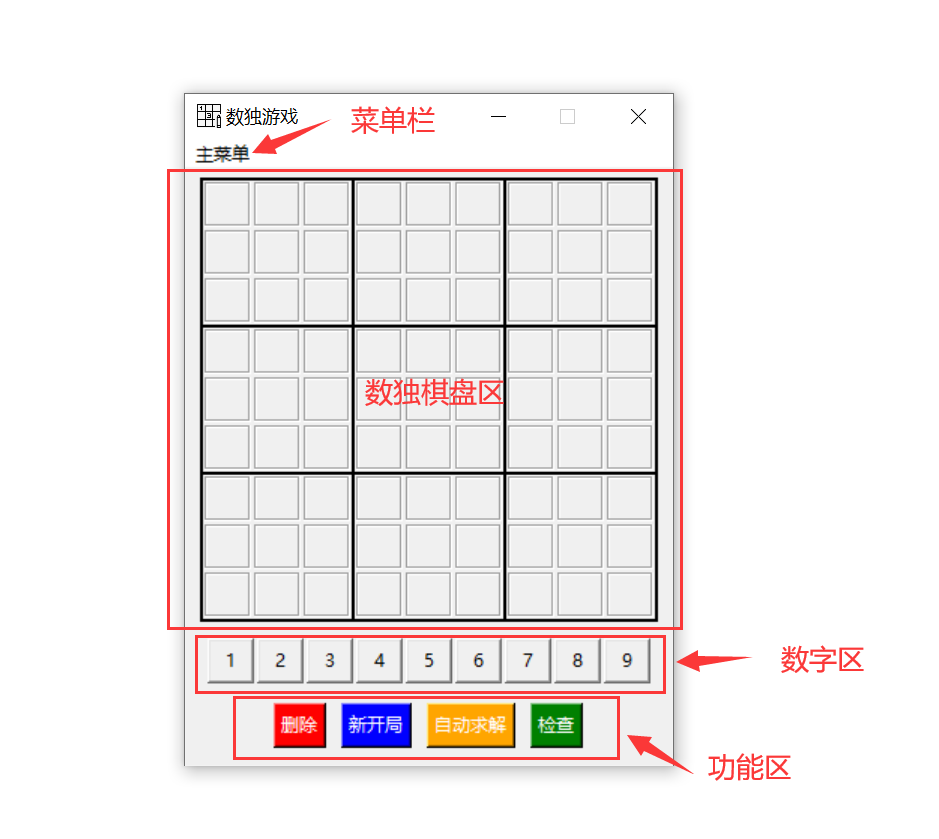
界面介绍 30
使用演示 32
参考文献 37
数独游戏
需求分析
生成
不重复
的数独终局至文件,并满足以下三个条件:
保证每一个数独终局左上角的第一个数字必须为 (1 + 3) % 9 + 1 = 5
所有数独终局不重复
生成1000个数独终局的时间限制在60s内
读取文件内的数独问题,求解并将结果输出到文件,需要满足以下条件:
求解1000个数独题的时间限制在60s内
解题思路
生成数独
我们知道,一个9×9的合法数独终局需要同时满足以下3个要求:
1.每行单元格包含整数1到9,且每个数恰好出现一次。
2.每列单元格包含整数1到9,且每个数恰好出现一次。
3.每个3×3的宫包含整数1到9,且每个数恰好出现一次。
经过查阅资料,我找到了生成数独终局的以下三种方法:
1.暴力搜索+回溯
2.矩阵变换法
3.全排列平移+行变换
对于上述三种方法,我们依次来分析。首先,方法1是通过不断的填数、检查和回溯去生成一个终局,而一般我们尽量避免使用暴力搜索的方法,因为虽然它们可以生成质量不错的数独终局,但是非常耗时。
对于方法2和方法3,我参考了这篇博客 - 数独终盘生成的几种方法 ,为了说明这两种方法,我先来介绍数独终局在交换方面拥有的3个性质:
1.交换9×9的合法数独终局的两列,如果被交换的两列同时在左三列或中间三列或右三列,那么交换后得到的数独终局是合法的。
2.交换9×9的合法数独终局的两行,如果被交换的两行同时在上三行或中间三列或下三行,那么交换后得到的数独终局是合法的。
3.将9×9的合法数独终局中的两个数字的全部位置兑换,得到的数独终局是合法的。例如交换数字1和数字2,即把所有填数字1的位置改为数字2,所有填数字2的位置改为数字1。
根据上述的三条性质,矩阵变换法的基本思想就形成了:选择一个初始的种子数独终局,根据上述三条性质,随机地对该数独终局进行交换,交换的次数不限,同时随机地对数独终局进行 0或90或180或2700或90或180或270 的旋转,则可以得到一个合法的数独终局。这种方法不仅效率高,实现方便,且生成的数独终局两两重复的概率很低。但是我认为该方法存在一个问题:对于这种随机的方法,虽然解空间很大,生成重复的终局概率很低,但是我们也无法从理论上证明生成的1000000个终局中不存在重复数独。因此我选择了第三个方法。
方法3的基本思想是:对数字1到9进行全排列,对于每一个排列情况,将其作为数独终局的第一行,然后从第2行开始,每一行的数字分别是第一行数字向右偏移3、6、1、4、7、2、5、8位,这样就可以生成一个合法的数独终局,然后利用交换性质,在第2和3行之间、第4、5、6行之间、第7、8、9行之间两两交换,要把所有的交换都遍历到且不重复。根据上述描述,在第一位数字确定的情况下,我们可以生成的终局有 8!×2!×3!×3!=29030408!×2!×3!×3!=2903040 个,这数量远超过1000000。因为在生成的过程中,无论是第一行的生成还是交换行的方法,我们都严格的把所有情况按照全排列的顺序遍历,所以生成的终局一定两两不重复。