立体匹配的成本函数评估-毕业作品网站

机器人与机电一体化研究所奥伯法芬霍芬德国航空航天中心（DLR）

摘要

立体匹配方法依赖于用于计算图像位置相似性的匹配成本。在本文中，我们评估了不同的匹配成本对于输入图像的辐射变化的不敏感性。我们考虑了像素变体和窗口变体的情况，同时在存在由增益和曝光差异导致的全局强度变化，由渐晕、非朗伯曲面以及不同光照导致的局部强度变化，以及噪音的不同情况下测量它们的性能。我们将通过具有地面实况差异的现有立体数据集，以及在受控的曝光和照明变化情况下拍摄的六个新数据集，采用局部、半全局和全局立体方法评估不同的成本。

1.介绍及相关工作

所有立体匹配算法都有一种测量图像位置相似性的方法。计算匹配成本通常会考虑到每个像素处所有差异。最简单的匹配成本会假设匹配图像位置处是恒定强度，但是更明显的成本模型会或明或暗地模拟某些辐射变化以及噪声。常见的基于像素的匹配成本包括灰度和彩色图像的绝对差异，平方差异，采样不敏感的绝对差异[2]，或截断版本。常见的基于窗口的匹配成本包括绝对差或平方差（SAD / SSD），归一化互相关（NCC）以及秩和普查变换之和[23]。使用过滤器可以有效地实现一些基于窗口的匹配成本。例如，可以使用秩滤波器获取结果，再通过结果的绝对差来计算秩变换。还有其他像LoG和均值滤波器等一样的过滤器可以尝试消除偏差或增益变化。

测量包括互联信息[7,9,11]和Zitnick等人在分层立体方法中使用的近似分段互联信息[24]等更加复杂的相似性也是是可能的。

最近的立体调查[5,17]和米德尔伯里在线评估[14]比较了最先进的几种立体方法带有复杂的几何形状和不同的纹理的测试数据。其他评估则侧重于像实时匹配的聚合方法[21]这些方面。然而，由于立体测试集通常是成对地辐射地测量非常相似的图像，因此测量过程不评估匹配成本的不敏感性。

专业术语“相似辐射度”是指在相同场景点处的像素在图像中所具有相似或理想相同的值。由于设置的稍微不同、渐晕、图像噪声等情况，相机可能会引起辐射差异。进一步的差异原因可能是因为非朗伯表面，这使得反射光的量取决于视角。最后，当在不同时间获取静态场景的图像时，使得光源的强度或位置可以改变，比如匹配天线或卫星图像的情况。在所有情况下，都需要能够处理辐射度差异的方法。

本文的范围是对几种具有常见辐射差异的图像进行一些广泛使用的立体匹配成本的评估和比较。重点是匹配显著或隐含处理辐射差异的成本。这排除了流行的方法，例如根据接近度和颜色相似性的基于相关性的加权[22]，因为这是一种使用截断的绝对差值作为匹配成本的聚合方法。此外，根据所考虑的应用，仅评估在具有未知辐射畸变和光源的单个立体对上工作的方法。这排除了通过采用至少两个具有不同照明的立体图像[6]或需要校准光源的方法来明确处理非朗伯曲面的方法。

2.匹配成本和立体方法

区分匹配成本和使用这些成本的方法很重要。在本文中，我们比较了6种成本和3种立体方法。我们考虑所有可能的组合来全面评估每种成本的不敏感性。

2.1.匹配成本

我们的第一个成本函数是常用的绝对差值，它假设相应像素的亮度恒定，并作为我们评估的基准性能指标。局部立体方法通常在窗口上聚合绝对差值之和（SAD），而全局方法使用像素方式的差异。在这两种情况下，我们使用Birchfield和Tomasi（BT）的不敏感采样方法进行计算[2]。

接下来的三个成本函数可以实现为单独应用于输入图像的过滤器。然后使用绝对差异匹配变换的图像。第一个滤波器是高斯拉普拉斯（LoG），它通常用于局部方法中去除噪声和偏差的变化[10,13]。在这里，我们使用标准偏差为1像素的LoG滤波器，该滤波器由卷积应用使用5×5内核。第二个滤波器是秩滤波器，它使某个社区的所有像素用其中的秩替换像素的强度。最初提出[23]对邻域内的异常值的鲁棒性，这通常发生在深度不连续附近并导致物体边界模糊。由于该方法仅取决于强度的顺序而不是它们的值，因此它补偿了所有保留的辐射畸变这个顺序。这里我们使用一个秩滤波器，其中一个15×15像素的方形窗口以聚焦的像素为中心。虽然还有其他基于秩的匹配方法[1,16]，但我们选择了秩变换，因为它可以有效地表现为滤波器，而无需改变立体方法本身。第三个滤波器是均值滤波器，旨在通过减去某个邻域的平均强度来补偿偏差的变化。我们再次使用尺寸为15×15的方形窗口，该窗口以聚焦的像素为中心。

我们的下一个匹配成本是互联信息（MI），一个处理两个图像之间复杂辐射关系的有效方法[20]。通过对每个图像的重叠部分的直方图的熵进行求和，并减去像素对应关系的联合直方图的熵来计算两个图像的MI。MI值直接表示图像的注册程度。这是由于观察到良好配准的图像的联合直方图仅具有几个高峰，而联合直方图相当平坦。因此，对于良好配准的图像，联合直方图的熵较低，而各个直方图的熵变化很小。MI已被用于本地[7]和全球[11]立体方法。在后一种情况下，其计算由泰勒展开变换，以获得像素方式的匹配成本。在成本矩阵中为每种强度组合存储成本。此查找表是匹配所必需的，但只能从已知的对应关系中创建。该解决方案是迭代设计，其中前一循环的视差图像用于创建在下一循环中匹配强度的成本矩阵[11]。该过程以随机视差图像开始，并且通常仅需要3到4次迭代。

在本文中，我们使用[9]的高效分层MI（HMI）方法，其工作原理如下。首先，两个输入图像按因子16缩小，并且通过使用随机视差图像匹配立体图像来计算MI。在对视差进行放大之前迭代该过程几次，以用作在全分辨率的 1 匹配的初始猜测。重复升级和匹配，直到达到完整分辨率。应当注意，较低分辨率级别的视差图像仅用于计算较高分辨率级别的匹配成本，而不用于限制视差范围。如果立体方法的运行时间线性地依赖于，则分层计算的运行时开销仅为14％像素数和差异[9]。

最后，我们还评估了归一化互相关（NCC）。NCC是用于匹配关键像素周围的两个窗口的标准方法。窗口内的归一化补偿了增益和偏差的差异。NCC在统计上是补偿高斯噪声的最佳方法。然而，NCC倾向于模糊深度不连续性而不是许多其他匹配成本，因为异常值导致NCC计算中的高误差。MNCC已被Moravec [15]引入作为常见变体。我们选择标准NCC，因为MNCC在我们的实验中给出了稍差的结果。与我们在此考虑的所有其他匹配成本相比，NCC由于其基于窗口的设计而只能与本地方法一起使用。

在上述所有成本中，我们仅使用图像强度（亮度）而不是颜色进行匹配。原因是所考虑的若干成本（例如等级和MI）自然地定义在强度图像上，并且为了公平起见，我们想要比较相同输入数据上的所有成本。但是，我们还发现，那些容易扩展到颜色的成本只能在我们的数据集上略微提高。显然，强大的色彩匹配需要未来进一步的研究。

总而言之，我们比较了六种成本：采样不敏感的绝对差值（BT），三种基于滤波器的成本（LoG，秩和平均值），分层互信息（HMI）和归一化互相关（NCC）。

2.2.立体算法

匹配成本的性能取决于使用成本的算法。因此，我们考虑三种不同的立体算法：局部的，基于相关的方法（Corr），半全局方法[9]（SGM），以及使用图切割[4]（GC）的全局方法。我们为每个立体方法实现了六种匹配成本中除了仅与本地方法一起使用的NCC的每一种。

我们的局部立体方法（Corr）是一种基于窗口的简单方法[10,13,17]。汇总匹配成本后使用9×9像素的方形窗口，选择具有最低聚合成本的差异（赢者通吃）。这是然后是子像素插值，左右一致性检查，用于使遮挡和不匹配无效，以及小于160像素的视差段的无效[8]。通过传播相邻的小（即背景）视差值来填充无效的视差区域。与比较“原始”结果相比，我们执行这些后处理步骤的原因是减少总体错误，从而改善成本之间的区别。

我们的第二个立体算法是半全局匹配（SGM）方法[9]。我们选择它作为本地和全球匹配之间的方法。此类别中还有其他方法，例如动态编程（DP），但SGM优于DP并且不会产生任何条纹伪影。SGM旨在最小化全球二维能量函数E（D）通过解决大量的1D最小化问题。在此[9]之后，实际使用的能量是

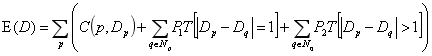（1）的第一项计算对于其差异Dp处的所有像素p的像素方式匹配成本C（p，Dp）（如2.1节中所定义）的总和。函数T[]被定义为如果其参数为真则返回1，否则返回0。就这样能量函数的第二项将p的相邻像素Np的小差异差异与成本P1进行惩罚。类似地，第三项以较高的惩罚P2来惩罚较大的差异步骤（即不连续性）。P2的值通过相邻像素p和q和公式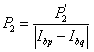

来适应局部强度梯度。这导致更加清晰深度不连续性，因为它们大多与强度变化一致。

SGM使用动态编程计算沿着从8个方向朝向每个关键像素的1D路径的E（D）。对于每个像素和视差，对所有路径的成本求和。然后由赢家通吃确定差异。执行子像素插值以及左右一致性检查。低于20像素大小的视差片段无效以消除小片异常值。再次插入无效的差异。

最后，我们使用图形切割（GC）立体算法作为全局方法的代表[3,4,12]。我们的实现基于[19]提供的MRF库。我们尝试使用与SGM相同的能量函数E（D）。但是，我们发现对于GC，它可以提供更好的结果使成本P2不与强度梯度线性相匹配，而是使P2的值加倍于给定阈值以下的梯度。与SGM一样，GC仅接近全球最小的E（D），但与SGM相比，它使用完整的2D连接作为平滑项，而SGM则是沿着1D路径单独划分。与Corr和SGM不同，我们的GC实现既不包括子像素插值也不包括遮挡。

我们使用没有辐射差异的图像为每个成本单独手动调整SGM和GC的平滑度参数。在调整阶段之后，所有图像和实验的所有参数都保持不变。这个方法允许专注于表现匹配成本而不是立体方法。

3.评估

我们测试了所有匹配成本的所有组合，以及具有模拟和实际辐射变化的图像上的局部、半全局和全局立体算法。

3.1.模拟辐射变化

对于我们的第一组实验，我们使用标准的Middlebury立体数据集Tsukuba，Venus，Teddy和Cones [17,18]。图1显示了每组的左图。所有图像是在实验室中仔细拍摄的相机设置和相同的照明条件下。因此，预计辐射变化将是最小的。我们使用了Tsukuba的16像素差异范围，Venus的32像素和Teddy和Cones的64像素。

第一个实验包括线性地（即增益变化）和非线性地（例如伽马变化）人为地改变全局亮度。只更改了正确的立体图像，同时保持左图像不变。此外，我们应用了模仿渐晕效果的局部亮度变化，即亮度随着到图像中心的距离成比例地减小。在两个立体图像上执行该变换。最后，我们用不同水平的高斯噪声污染了两个立体图像。

在计算了所有变换的视差图像以及匹配成本和立体算法的所有组合之后，我们通过计算具有与地面实况相差超过1的差异的像素数来评估结果。在我们的统计中，我们忽略了遮挡区域，因为GC实现不考虑遮挡（与Corr和SGM相反）。对于相关结果，我们还忽略了图像边界处的4个像素（相关窗口的一半）的区域。我们的最终误差测量是所有四个数据集的平均误差百分比。图2将这些误差绘制为匹配成本和立体方法的每种组合的强度变化量的函数。我们现在讨论个别结果。

图2a比较了与亮度降低的图像相关性时的匹配成本。随着亮度的降低，BT的误差会迅速增加。这是可以预期的，因为绝对差异基于相应像素具有相同值的假设，这是违反的。均值和LoG滤波器可以补偿一些差异，但会降低。当s <0.5时迅速，两个滤波器都设计用于补偿偏置（即恒定偏移），但不是增益（即规模）变化。NCC，HMI和Rank表现出非常稳定的性能，直到错误突然增加。从理论上讲，这三种方法都应该能够完全补偿亮度的变化。增加误差的原因是变换后的图像被存储为8位。因此，还存在信息丢失，s值较低。

继续下两个图，可以看出SGM和GC（图2b-c）通常比相关性更好。不同匹配成本的相对性能仍然相似，尽管对于SGM，LoG成本现在略微优于未变换图像上的Rank（即，比例因子为1）。一个更重要的观察结果是HMI的性能比具有相关性的Rank差，但是使用SGM和GC要好得多。可能的原因是Rank还降低了深度不连续点附近异常值的影响。这对于基于窗口的方法很重要，但对于像SGM和GC这样的基于像素的方法则不那么重要。有趣的是，在非转换图像上，HMI的性能优于BT，特别是对于SGM和GC（图2b-c）。可以假设BT对于没有任何辐射差异的图像应该是最佳的。然而，即使图像是在受控条件下拍摄的，一些辐射度差异是固有的，表面也不是朗伯的，并且仍然违反了亮度恒定性假设。HMI放松了这个假设并且只期望全局一致的映射。

接下来的三个图（图2d-f）显示了伽马变化的影响，作为亮度非线性变化的一个例子。结果类似于线性变化的情况，尽管NCC的性能随着伽马变化的增加而降低。

除了HMI之外，人工渐晕效果（图2g-i）与全局亮度变化相比给出了非常相似的曲线。HMI性能相当差的原因在于其成本明确地基于复杂但全局辐射变换的假设。渐晕效果局部改变亮度。过滤器解决方案LoG和Mean也假设全局变化，但仅在其相当小的窗口内。此外，Rank仅需要保持不变的订单。因此，滤波器解决方案，尤其是Rank，在局部放射性强变化的情况下最佳。

最后，在最后三个图中显示了具有变化的信噪比（SNR）的加性高斯噪声的结果（图2j-1）。SNR值越高意味着噪声越低。对于相关性，不同的成本执行非常相似，可能是因为在固定窗口上求和就像平均一样，这降低了高斯噪声的影响。SGM和GC的情况不同，其中LoG，Rank和Mean表现甚至比BT差。HMI在所有噪声级别上始终优于SGM和GC。

总结上述实验，Rank似乎是基于相关性的方法的最佳匹配成本。在全局亮度变化和噪声存在的情况下，HMI似乎最适合基于像素的匹配方法，如SGM和GC。在局部亮度变化（例如渐晕）的情况下，Rank和LoG似乎是比HMI更好的选择。

3.2.真实曝光和光源变化

如引言中所述，现有的立体测试数据集非常放射性地“干净”，并且不需要实际立体应用所需的强大匹配成本（除非像上一节那样，综合引入了变化）。为了解决这种情况，我们使用[18]的结构化照明技术创建了几个具有基本事实的新立体数据集，可在http://vision.middlebury.edu/stereo/data/中获取。在本文中，我们使用图3中显示的六个数据集：Art，Books，Dolls，Laundry，Moebius和Reindeer。每个数据集包括从沿线的等距点获取的7个校正视图，以及视点2和6的地面实况视差图。在本文中我们仅考虑双目方法，因此我们使用图像2和6作为左右输入图片。此外，我们将原始图像下采样到它们大小的三分之一，导致大约460×370像素的图像有80像素的差异范围。在创建数据集时，我们使用三个不同的展览拍摄每个图像确保光源和三种不同配置的光源。因此，我们从每个视点有9个不同的图像，这些图像表现出显着的辐射差图4显示了Art数据集左图像的曝光和光照变化。

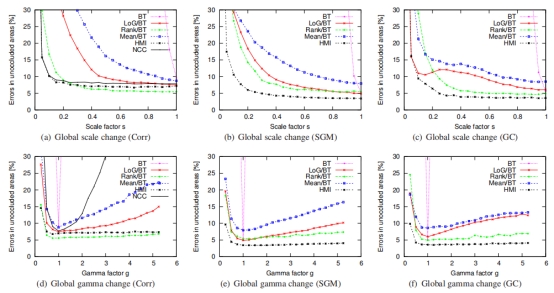
图2.对Tsukuba，Venus，Teddy和Cones数据集应用辐射变化或噪声的影响。列对应于三种立体方法，而每行表示检查不同类型的强度变化。

我们测试了匹配成本和立体声的所有组合所有3×3曝光和光变组合的算法。总匹配误差如前所述计算为所有六个数据集的异常值的平均百分比（视差误差> 1）。得到的曲线如图5所示。应该注意的是，由于增加了视差范围，缺乏纹理，以及更复杂的场景几何使得我们的新图像比第3.1节中使用的图像更具挑战性。这反映在较高的匹配误差中：最好的方法现在具有大约10％的误差，而不是之前的大约3％。

图3.具有基本事实的新艺术，书籍，玩偶，洗衣，莫比乌斯和驯鹿立体测试图像。

图4.具有三种不同曝光和三种不同光照条件的Art数据集的左图。

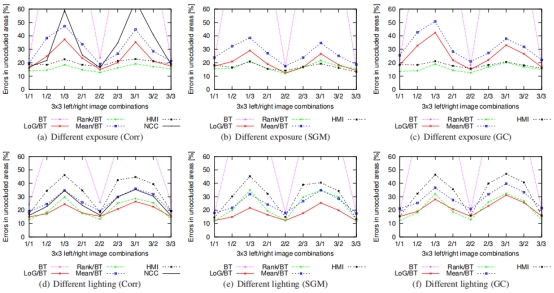
图5.匹配曝光或照明条件不同的3×3左/右图像组合。给出的是平均误差。

图5a显示了在具有不同曝光设置的图片上使用所有匹配成本和相关性的结果。曝光的变化是一种全局变换，类似于全球亮度变化。因此，观察结果与图2a和2d中的观察结果相似并不令人惊讶。即Rank和HMI表现最佳，而LoG和Mean有更多问题，因为它们不是为补偿增益变化而设计的。主要区别在于NCC的糟糕表现。与SGM和GC匹配成本的性能如图5b-c所示。与3.1节相比，Rank的性能略好于HMI，特别是在具有相同曝光设置的情况下。此外，相关情况下Rank的表现略差于与全球方法结合情况下Rank的表现。原因可能是Rank对异常值的鲁棒性有助于这两个具有挑战性的场景。

改变光源的位置会导致许多局部辐射测量差异。相关结果（图5d）证实所有匹配成本都存在这些严重变化的问题。然而，Rank和LoG再次最佳，而HMI仅比BT更好。这与人工渐晕效果基本相同（图2g）。SGM和GC的情况类似（图5e-f），其中Rank和LoG也是表现最佳的成本。HMI显然存在更多照明变化的问题，导致局部亮度变化，不能表示为全局变换。

3.3.定性评估

我们在3.1节中注意到，即使在没有任何额外辐射变换的原始图像上，匹配成本之间也存在性能差异。为了对这些差异进行定性分析，我们检查了所有图像对上匹配成本和算法的所有组合的视差图。

由于空间限制，我们仅为Teddy图像对显示完整的视差图集（图6）。乍一看，所有相关结果看起来都相似（图6a-f）。但是，在BT结果中可以看到更多错误。此外，在观察烟囱时，Rank和HMI似乎在深度不连续处造成较少的扭曲。这证实了3.1节中Rank和HMI表现最佳的结果。对于SGM，差异更大（图6G-K）。BT和HMI产生最佳的物体边界，而LoG，Rank，尤其是均值滤波器会导致物体边界的扭曲。GC的效果类似（图61-p）。回想一下，GC的实施不包括对闭塞的治疗；因此，应忽略留给对象边界的错误。我们在其他图像对上发现了类似的行为。

3.4.运行

许多应用程序不仅要求准确的差异，还要求快速的运行时间。表1给出了Teddy图像对的LoG，Rank和HMI计算（不包括立体方法的运行时）的运行时间。所有的方法都是

在具有2.8 GHz的Pentium 4上测量。Teddy图像的大小为450×375像素。LoG滤波器使用5×5内核，Rank滤波器使用15×15内核。100 ms HMI的运行时间包括升级时间

缩小图像以及所有层次级别的MI计算，从完整图像大小的 1 开始。另外，立体方法不仅需要在全分辨率图像上运行，还需要在缩小尺寸的图像上运行。对于Corr和SGM，在全分辨率下测量的开销大约为其运行时间的15％。

方法	LoG	Rank	HMI
开销	20ms	35ms	≈100ms+15%
实施	C/MMX	C/MMX	C

应用均值滤波器或NCC所需的时间不包括在内，因为这些方法是用Java实现的，并没有进行优化。

4.结论

我们比较了几种不同的成本函数，用于放射性不同图像上的立体匹配。使用三种不同的立体算法评估每个成本：局部相关方法，半全局匹配方法和使用图切割的全局方法。我们发现匹配成本函数的性能取决于使用它的立体方法。在具有模拟和实际辐射度差异的图像上，秩变换似乎是基于相关的方法的最佳成本。在具有全局辐射变化或噪声的测试中，分层互信息对于基于像素的全局匹配方法（如SGM和GC）表现最佳。在存在局部辐射变化的情况下，Rank和LoG比SGM和GC的HMI表现更好。

对没有辐射变换的图像的视差图像进行定性评估表明，基于滤波器的成本（LoG，Rank和Mean）倾向于模糊对象边界。这不会影响相关结果，因为固定大小的相关窗口无论如何都会导致模糊的不连续性。相反，这些滤波器实际上可以解决这个问题，特别是秩滤波器，它可以减少不连续点附近异常值的权重。但是，对于基于像素的匹配方法（如SGM和GC），模糊效果清晰可见。对于这样的方法，BT和HMI的结果看起来最好。

我们所比较的匹配成本中没有一个在处理由改变光源位置引起的强烈的局部辐射变化方面非常成功。如果可以将不同成本的优势结合起来以获得能够处理像Rank和LoG这样的局部辐射变换的匹配成本同时仍然保持像HMI那样的尖锐深度不连续性，那将是很好的。

未来的工作包括测试可以处理辐射度差异的其他匹配成本，例如人口普查变换[23]和Zitnick等人的MI近似[24]。

致谢

我们要感谢Anna Blasiak和Jeff Wehrwein帮助创建本文中使用的数据集。

参考

[1] D. Bhat, S. Nayar, and A. Gupta. Motion estimation usingordinal measures. In Proc. CVPR, 1997.

[2] S. Birchfield and C. Tomasi. A pixel dissimilarity measurethat is insensitive to image sampling. TPAMI, 20(4):401-406, 199.

[3] Y. Boykov and V. Kolmogorov. An experimental comparisonof min-cut/max-flow algorithms for energy minimization invision. TPAMI, 26(9):1124–1137, 2004.

[4] Y. Boykov, O. Veksler, and R. Zabih. Fast approximate energy minimization via graph cuts. TPAMI, 23(11):1222–1239, 2001.

[5] M. Z. Brown, D. Burschka, and G. D. Hager. Advances incomputational stereo. TPAMI, 25(8):993–1008, 2003.

[6] J. Davis, R. Yang, and L. Wang. BRDF invariant stereo usinglight transport constancy. In Proc. ICCV, 2005.

[7] G. Egnal. Mutual information as a stereo correspondencemeasure. Technical Report MS-CIS-00-20, Comp. and Inf.Science, U. of Pennsylvania, 2000.

[8] H. Hirschm¨uller. Stereo Vision Based Mapping and Immediate Virtual Walkthroughs. PhD thesis, School of Computing,De Montfort University, Leicester, UK, 2003.

[9] H. Hirschm¨uller. Accurate and efficient stereo processingby semi-global matching and mutual information. In Proc.CVRP, volume 2, pages 807–814, 2005.

[10] H. Hirschm¨uller, P. R. Innocent, and J. M. Garibaldi. Realtime correlation-based stereo vision with reduced border errors. IJCV, 47(1/2/3):229–246, 2002.

[11] J. Kim, V. Kolmogorov, and R. Zabih. Visual correspondenceusing energy minimization and mutual information. In Proc.ICCV, 2003.

[12] V. Kolmogorov and R. Zabih. What energy functions can beminimized via graph cuts? TPAMI, 26(2):147–159, 2004.

[13] K. Konolige. Small vision systems: Hardware and implementation. In Proc. ISRR, pages 203–212, 1997.

[15] H. Moravec. Toward automatic visual obstacle avoidance. InProc. Joint Conf. on Artif. Intell., pages 584–590, 1977.

[16] R. Sara and R. Bajcsy. On occluding contour artifacts instereo vision. In Proc. CVPR, 1997.

[18]. Scharstein and R. Szeliski. High-accuracy stereo depthmaps using structured light. In Proc. CVPR, volume 1, pages195–202, 2003.

[19] R. Szeliski, E. Zabih, D. Scharstein, O. Veksler, V. Kolmogorov, A. Agrawala, M. Tappen, and C. Rother. A comparative study of energy minimization methods for Markovrandom fields. In Proc. ECCV, volume 2, pages 16–29, 2006.

[21] L. Wang, M. Gong, M. Gong, and R. Yang. How far can wego with local optimization in real-time stereo matching. InProc. 3DPVT, 2006.

[22] K.-J. Yoon and I.-S. Kweon. Adaptive support-weight approach for correspondence search. TPAMI, 28(4):650–656,2006.

[23] R. Zabih and J. Woodfill. Non-parametric local transformsfor computing visual correspondance. In Proc. ECCV, pages151–158, 1994.

[24] C. L. Zitnick, S. B. Kang, M. Uyttendaele, S. Winder, andR. Szeliski. High-quality video view interpolation using alayered representation. In SIGGRAPH, 2004.