Jounal of matenals processing technology 63 (1997) 881-886

Experiment and study into the axial drifting of the cylinder

of a welding rollerbed

Fenggang shen ,xide pan ,jin xue

Welding research instiute ,xi`an jiaotong university. Xi`an .shaanxi province 710049.P.R.china

Abstract

The basic theory of the axial drifting of the cylinder of a welding roller bed is introduced in the paper,and at the same time experiment and study on the mechanism of the axial drifting of the cylinder have been done on an experimental model of the welding roller bed . It is shown that the main cause of the axial drifting of the cylinder lies in the existence of a spiral angle between the cylinder and the cylinder and the roller . the relative axial motions between the roller and the cylinder are compose of spiral motion,elastic sliding and frictional sliding. The theory of compatible motion and non-compatible motion is put forward for the axial motions of the cylinder .the relative axial motions of the cylinder . The relative axial motion between the rollers and the cylinder is coordinated by elastic sliding and frictional sliding between them

Keywords: welding roller bed; cylinder ; roller ; axial motion ; spiral angle

1  Introduction

In welding production, the assembly and circular seam welding of rotary workpieces, such as a  boiler, a  petrochemical pressure vessel and  so on, are conducted on ;a welding  roller  bed.  When rotating On a welding roller bed. The cylinde will inevitably produce axial drifting due to manufacturing, assembling tolerance of the welding roller bed and the cylinder’s surface  irregularity (divergiug froman ideal rotary workpiece),  thus the welding procedure may not be carried out successfully. It is necessary, therefore, to study the mechanism of the axial  drifting of the cylinder to solve the problem of the axial drifting of the cylinder in circumferential welding. The results of the research will benefit the studying and designing of antidrifting welding roller  bed. especially the analysis of the applied forces on the bed, and lead to determining the manufacturing and assembling tolerance of the bed,  and  providing the basis of theory for the mechanical adjusting mode to avoid axial  drifting,  the  adjusting mode of closed circuit  in the control  circuit, and the selection of  the  adjusting  value.

2.  Theoretical analysis

2.1. Welding roller bed and cylinder

A welding roller bed is generally composed of four rollers. Driven by the  driving roller, the cylinder makes a rotary uniform motion around its axis(shown in  Fig.  I), during which  the  circumferential welding procedure is carried out In  Fig.1, a is the central angle, S is the supporting distance, L is the span of the  roller. and V, is the circular linear velocity of the cylinder, also named the welding velocity2.

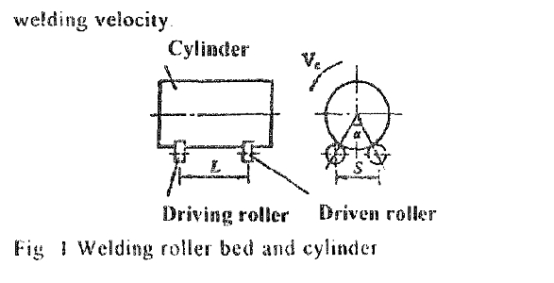
The axis of the cylinder will be not parallel to that of a roller if the roller is deflected by a certain  angle from the deal position, or if  the centers of the four rollers lie in the vertices of a simple  quadrilateral, or if the centers of the four rollers are not on the same plane, or if the circu- larity  of the cylinder is irregular because of deviation in manufacturing and assembling. Thus. the  cylinder will nevitably move along its axis when rotating on a bed the contact of the cylinder  and a roller can be cansidered as point contact if cytinder’s axis and roller’s axis do not lie in the  same plane. Suppose P is the point of contact. the cylinder’s normal plane A is defined by the  plane on which are the cylinder’s axis and generatrix n across the point of tangency on the  cylinder (shown in fig2) makea cylinder’s tangent plane B across point P.  Thus, plane A is  vertical to plane B. lc is a cylinder’s tangent across P and lies in plane  B. Ir is the roller’s  tangent across the same point P, and lies in plane B also. In  general, θ is

defined as the axial deviation angle between the rol!er’saxis and the cylinder’s  axis; β is defined as the spiral angle between generatrix n and m’ . a projective line obtained by projecting the roller’s generatrix m across point p on plane B and γ is defined as the projective angle between n and m , a projective line obtained byprojecting m on plane A. Fig. 3 indicates that the rela- tionship amongst the three  angles is tanβ = tan2θ -  tan 2γ

In Fig. 3, SB, Sθ and Sγ, are called the spiral displace-ment vector, the axial  deviation displacement vector and the projective displacement vector respectively.  their

relationship being:

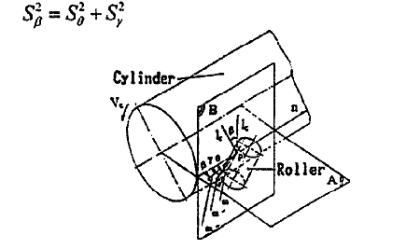
Fig. 2 Geometric relationship between the cylinder and an

individual roller

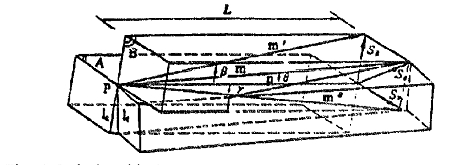
Fig. 3 Relationship between the angle vector and the

displacement vector

2.2.2 relative axial motions relationship

(1)spiral motion2.

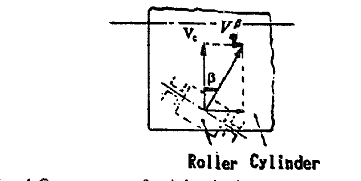
Fig. 4 Component of axial velocity

Because the roller’s axis is not parallel to the cylin- der’s central line, there is a spiral angle β between Vr,. and Vc, on the point of contact (shown  in  Fig.  2).  When the roller and cylinder rotate synchronistically around their own axes,  driven  by tangential frictional force. a spiral effect will occur because  of  the  different  linear velocity direction between the roller and the cylinder at point P of contact The  cylinder has a component of axial velocity,

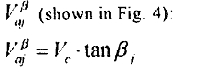
where Vc is the circular linear velocity of the cylinder. 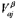 is the cylinder’s axial  component velociry exerted by single roller, and j can be 1. 2, 3, 4, representing the   four rollers, respectively.

(2) Elastic sliding

Because of the existence of a spiral angle, an axial force Faj acts on cylinder.  When  the force is less than the maximum axial frictional force fNj (where f is the frictionfactor, and Nj is the normal pressure between a single roller and the  cylinder),  the cylinder will  slide elastically over the roller along the axial  direction[2~3]  The component of the sliding velocity is.

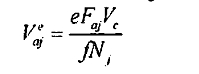
where e is the elastic sliding factor for metallic roller. e=O.OOl  ~~  0.005.

(3) Frictional sliding

When Faj is greater than the maximum frictional force fNj, the cylinder will make a  frictional sliding over the roller. The sliding resistance is fNj[3]. The component of   the frictional sliding velocity on Cylinder is Vaj the magnitude and direction of  which can be determined by the universal relationship between the  cylinder  and  the four rollers Frictional sliding will lead to the wear and tear of the surface of  the  cylinder and the rollers. which is unexpected in welding production  When  the  cylinder drifts, above three kinds of motion

do not occur simultaneously ‘I’hereforc. the axial drifting velocity of the cylinder is not the algebraic sum of the three components of velocity In  the case of  elastic  sliding, the axial velocity is.

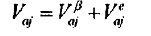
2.3 axial motion of the cylinder on a welding roller bed

2.3.1 Axial  compatible motion

Under ideal conditions, when spiral angles βj between the cylinder and  the four  rollers are all the same, that is:

β1=β2=β3=β4=β

the cylinder will move its compatible spiral  motion. Two categories can be classified to analyze  the  axial  motion of  the cylinder:

(I)  When there does not exist an axial component due to gravity. the cylinder’s axial drifting velocity is:

Va=Vc * tanβ

(2) When there exists an axial component of gravity Ga there exists an axial force  on the cylinder. Now, the axial forces exerted on the four  rollers  have  the  same directional

And magnitude, the value being equal to Ga besues the component of spiral vetocity, there exist component of elastic on the cylinder the cylinder`s axial drifting velocity is

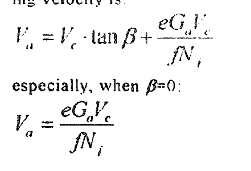
2.3.2.axial non-compatible motion

In general. spiral angles βj between the cylinder and the four rollers are not equal  to each other in size and direction. i .e. the geometric relationships between the cylinder and the four rollers  are all inconsistent Therefore, the components of  the  cylinder’s axial velocity against four rollers (i.e Vc *taβj) are not identical to each another. The cylinder will move with axial nompatible motion The axial  velocities  of the cylinder  againsa  the  four

rollers should be the same because the cylinder is considered as a rigid body as a  whole and it has only one axial velocity.  However. for some roller, Vc . tanβj and the cylinder’s real axial velocity are not likely to be the same, so an  axial frictional  force  almost  certainly  appears  between  this  roller and the cylinder  The  following two categories can be classified to discuss the  non-compatible axial  motion of the cylinder according to Ihe frictional force’s magnitude:

(I) When the axial frictional forces erected by each roller and the cylinder are  all less than the maximum axial the action of the cylinder against the  frictional force the action of the cylinder against the rollers produces elastic  sliding The axial  motion betweenan individual roller and the  cylinder  is  coordinated by their elastic sliding

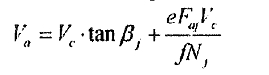
when the axial velocity of the cylinder is constant, the algebraic sum of cylinder’s  axial forces erected by four rollers should be zero if rhe axial  component  of  gravity is ignored. i.e.

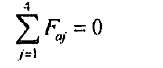
and there is little difference amongst Nj, against the four rollers, so that they can  be  approximately regarded as the same. Thus:

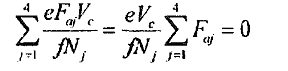
according to the above two equations, the axial drifting velocity of the cylinder is.

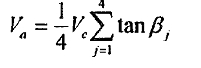
Where 0.25∑Tanβt  represents the intrinsic attributes of the welding. Other bed under the condition that only the cylinder against all rolls produces elastic sliding this may be called the spiral rate of the cylinder`s spiral motion

(2) When the axial frictional force erected by some roller and the cylinder is  greater  than the maximum axial frictional force, frictional sliding occurs between the cylinder and this roller Then. the maximum axial force is acting on the  bearing of the roller, its value being

Ffmax=fFNfmax

Because of the esistence of this frictional sliding. the Axial motion between an individual roller and the cylinder is not coordinated by their elastic  sliding  Now  the axial  non-compatible motion of the cylinder is determined by

the relative relationships between the cylinder and the four rollers. It is difficult to  write a general compatible equation of the cylinder’s axial drifting velocity  because this kind of condition  is very complex. The following is further  analysis and  discussion of the problem At  first,  for ease in analyzing problem,  the spiral  angle average is defined as

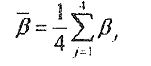
and the relative spiral angle as

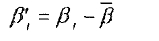
Arrange ,β1 in the order from big to smll and  then from posirive to negative,  expressed as β(j). then  β1≥β2≥β3≥β4

Similarly, the normal force between the cylinder and a roller can be expressed as  N(j). and the axial force as

Fj≤fNj

In general, the axial motion of the cylinder determined by the spiral angle average β is  definel as the compatible component of the axial motion,  is velocity  being

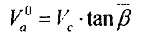
The axial motion of the cylinder determined by the relative spiral angle  βj  is  defined as the non-compatible component of axial motion, its velocity being  expressed asVa\n Analysis shows that Va`` is determined by the equilibrium  condition the four roller axial forces  when  the  cylinder  moves  along  axial  direction at a constant velocity. where not taking  into account of  the function of  gravity’s axial component. Supposing that the cylinder makes a  non-compatible component of axial motion with the maximum relative  spiral angle  β(I). its  velocity is

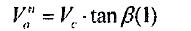
Then the four axial forces can not be in equlibrium .i.e

F1-(F2+F3+F4) ≤0

Because there is little difference amongst four normal forces, the four axial farces  are also determined by normal force and the  friction  factor any  axial  force  undoubtedly being less than the sum of the other three forces. Otherwise, if the  cylinder makes a non-compatible component of axial motion with the  minimum  relative spiral  angle  β(4).  its velocity  is.

Va” = Vc * tanβ(4)

Similarly. four axial forces can not be in equilibrium also, i.e. :

[F(l)  + F(2)  + F(3) J  - F(4)  > 0

Therefore, the cylinder can only be approximately considered as making a  non-compatible component of axial motion with the second or third  relative  spiral  angle,  i.e.:

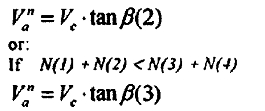
In whatever case as expressed above. when the cylinder make a non-compatible  component of axial  motion, thetwo rollers having a greater velocity  are  driving  rollers,and the other two rollers having a lesser velocity are resistant  rollers, the  equilibrium  condition of axial forces being operative, i.e.:

F(1) + F(2) = F(3) + F(4)

According to the analysis above, and because of the unstability of friction factor f  that is affected by the factors of load, material, condition of the contact surface, and  circumstance, the non-compatible component Va of the axial velocity of the  cylinder  is undefined. When the cylinder  makes a non-compatible axial motion,  its  axial  velocity is composed of a compatible

component Va\0 and a non-compatible component Va\n  i.e

Va=Va\0+Va\n

Va=Va\0+Va\n

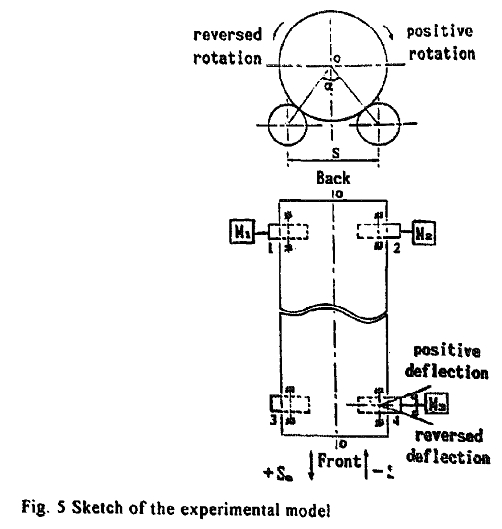
The most optimal adjustment of the axial motion is  to make the non-compatible  component as small as possible according to the stability of adjustment and decrease in axial force. No matter whether the cylinder  makes compatible or non-compatible  motion, supposing that the cylinder  is ideal, its axial velocity is  always  existent  and definable for a particular  bed, its magnitude and direction reflecting the bed’s  inherent property.

3.  Experiment

3.1.  Descriphm of experment

The experimental model is shown in Fig 5.  Experiments were done to study two  factors: the spiral angle and the cylinder’s  circular linear velocity, which affect the  axial drifting of the cylinder. In the experimenting process. the axial  displacement  Sa and the axial drifting velocity Va of  the cylinder were measured by the  variation of the two

factors described above. The measuring method is shown in Fig. 5, and is carried  out by means of bringing an axial displacement sensor into contact with one end of  the cylinder. with the sensor being connected to an X-Y recorder to  record  the  cylinder’s axial displacement every 5s. Linearly regressing the plot Sa--t  (t  expresses time), the average drifting velocity Va, at every deflecting  angle  can  be calculated.

Before experimenting. the experimental model is initialised as follows: first. the  height of the four rollers is adusted by means of a level to put  the  centers  of  the four

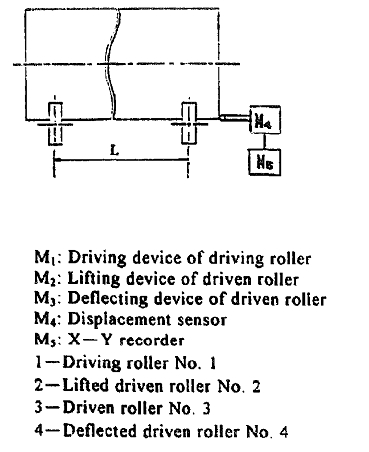
rollers in the same horizontal plane, and at the four  vertexes of the rectangle.  then  the rollers are deflected so that the rotating cylinder is at the relative equilibrium position. Then the cylinder does not drift over a long time. or periodically drift  over  a very small axial range

3.2 experiment results and discussion

3.2.1 Effect of spiral angle (I) Fig. 6 shows that change of Va with the variation ofThe  testing condition is: positive rotalion, Vc=35m/h

L=422mm,  α=60”

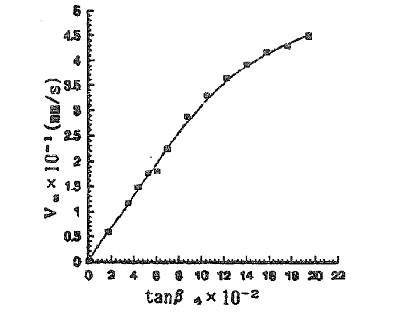
The Va-tanβ4 curve shows that Va is directly proportional to tanβ4 whenβ4 is relatively small  (1~~~6c ). The slope of the line being 3. 06 mm/s, Va  is no  longer direclly proportional to tanβ4 when β4,  is greater than 6C  The  curve  is an arched curve. i. e . with the increment of β4,.Va, increases. but with the  increment of Va gradually becoming smallet Because only one driven  roller (roller  No. 4) is deflected, i.e β4 can be changed whilst the others remain zero, the  cylinder makes a non-compatible motion. When β4 is relatively small,  Va   is  small also. The axial  frictional forces between the cylinder and rollers are less  than the maximum axial frictional force, and the cylinder produces  an  elastic  sliding against rollers. Axial motion between each roller and the cylinder is  coordinated by elastic sliding. thus Va is:

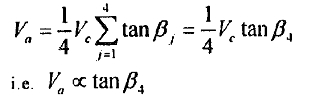
in the theoretical curve, the slope K’ can be calculated by

the following equation:

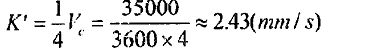
K=3.06mm/s in the experimental curve. Thus, in taking account of the  experimental  tolerance, the two slopes can be considered to be approximately equal.  When β4  is relatively large, the axial frictional forces between the cylinder and the rollers are  larger than the maximum axial frictional Force, and cylinder produces frictional  sliding against the rollers Because of Ihe existence of sliding  frictional resistance. Va is no longer  lincarty increased with the increment of tanβ4  With  the  increment of tanβ4 the increment of V a; with gradually become smaller

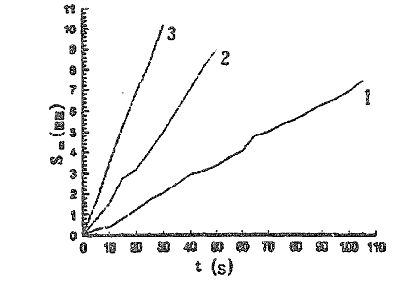
(2) The following three experiments were arranged to study the cylinder’s  non-compatible axial motion further, deflecting positively one roller. two  rollers  and three rollers by the same spiral angle to measure three curves  between Sa and  v The experimental results are shown in Fig 7. With  the increment  in the  number of deflected rollers, Va becomes greater. i e Va 3 > Va 2 > Va1

When  the number of driven rollers deflected  is varied, the degree  of the  cylinder’s non-compatible axial motion will be changed. With the increment of the  number of lollers deflected by the same spiral angle. the compatible component  becomes greater, but the non-compatible component  becomes smaller. In other  words, the cylinder’s axial motion will be transformed from noncompatible motion  to compatible motion. Thus, Va  becomes greater also, ultimately,  being  equal  to the compatible axial velocity determined by the spiral angle β Now. the four  rollers have the same spiral anyle β. So that Va is:

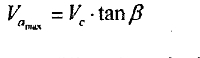
3.2.2 effect of circular linear velocity

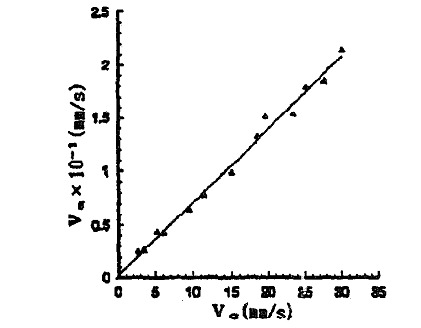
Deflecting driven roller No 4 to a spiral angle of +2”from the equilibrium position,  the cylinder will suffer axial drifting, Fig. 8 shows the Va-Vc curve, which latter indicates that Va is directly proportional  to Vc, the slope of the  curve  being  approximately 0.00708 because β4=+2 is too small, the cylinder does not make  frictional sliding against each roller. Thus, the relative axial motion  between  the  roller and the cylinder is completely coordinated by their elastic sliding, so that  Va  is

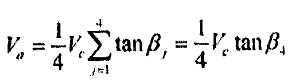
I. e .Va is directly proportional to Ve For the theoretical Curve the slope  K *  can be calculated by the following equation K”=0.25tanβ4=  0.25tan2'=0.00873 where K=0.00708mm/s  in  the  experimental  curve.  Thus, in taking account of the experimental tolerance, the two slopes can  be  considered to be approximately equal.

4  Conclusions

1. Because of the deviations due to manufacturing and assembling. the cylinder’s  central line and the  roller’s axis are not parallel.  i. e  , they are not  in  the  same plane, and there is a spiral angleβ at thc  point of contact between the  cylinder and the roller in the circular linear velocity direction. The  existence  of  βis the basic reason for the occurrence of axial  drifting. The effect of gravity in  cylinder’s axial direction is also one of reasons for drifting.

2. The relative axial motions between an individual roller and the cylinder are  composed of spiral motion. elastic sliding and frictional sliding When  axial  frictional sliding does not occur between the cylinder and a single

roller, the relative axial motion between the rollers and the cylinder is completely  coordinated by their elastic sliding, Va is directly proportional to

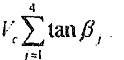
When axial frictional sliding occurs between the cylinder and a roller. the relative  asial motion between therollers and the cylinder will be commonly  coordinated  by  elastic sliding and frictional sliding. but Va  is  not

directly proportional to

3 The axial motions of the cylinder can be divided intocompatibleand  non-compatible motion There will be large axial forces acting on the bearings of the rollers, which will cause the wear and tear of the contact surfaces of the rollers and the cylinder, when non-compatible motion exists The non-compatible  component of the axial motion is undefined however. the cylinder’s axial velocity is always existent and definable for a particular bed, its magnitude and direction reflecting  the  bed’s  inherent  property.

4 The reasonable adjustment of the axial motion is  to make the  non-compatible  component as small as possible and the compatible component as large  as possible.

5 With the  increment  of the number of rollers deflected by the same value of β  the compatible component of axial velocity increases, but the  non-compatible  component decreases. With the increment of the compatible component, the velocity of axial drifting of the cylinder increases

References

(1) Z Wang(ed  ). teaching material on welding machinery Equipment Gansu university of Technology lanzhou P  R china  (1992)  pp  85-98

(2)Wuhan lnstitulcof Buildins Materials and TechnologyI Tongi Universily.  Nanjing Institute of Chemical Engineering, and Huanan Institute of  Technology.  Cement Producing machinery equipment, Architectural Industrial Publishing  House  of  China, Beijing,  (1981)  pp,  184-187

(3)J . Halling(ed.). Principles of Trilrology The Macmillan Press,  (1975)  pp.  174-200