Python时间序列选择波动率预测指数收益算法分析案例数据分析报告
背景
在传统的金融理论中，理性和同质的投资者是核心假设之一，表明每个投资者都有相同的信息，从而做出同样的决定。然而，投资者显然是不均衡的，信息的不对称在股市中很普遍。当知情投资者优先考虑某种类型的资产时，该类资产可能包含更多隐含信息。
期权市场是知情投资者可能更积极参与的市场之一，正如布莱克在1975年提出的那样，让投资者倾向于以较高的杠杆率而非股票本身交易股票衍生品以获得更多利益，因此期权市场可以包含更多信息。提取这些额外信息的一种方法是仔细研究波动性假笑。
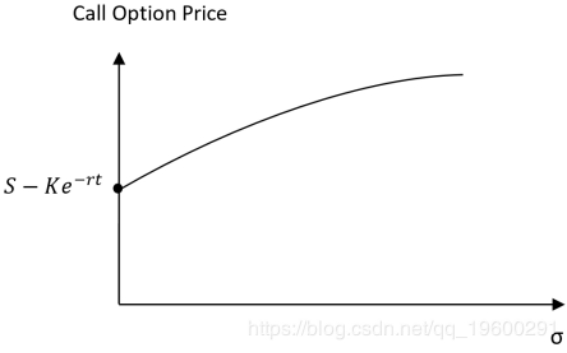
波动性 是我们都熟悉的，Pan（2002）的一个主流理论指出，假笑的主要原因是投资者厌恶跳跃风险引起的风险溢价，尤其是OTM看跌期权的情况。该文假设知情的交易者认识到跳跃风险，对OTM看跌期权的需求越多，跳跃风险溢价就越高。因此，我们定义
波动率偏差= OTM认沽期权隐含波动率 - ATM看涨期权隐含波动率，
我们在这里验证指数期权波动率偏差是未来指数收益的一个很好的指标。
美国市场
对于美国市场的实证研究，本文使用SPX期权，这是一种现金结算的欧式期权。从学术数据库OptionMetrics中检索2006-2012的选项数据。其中一些列在下面。
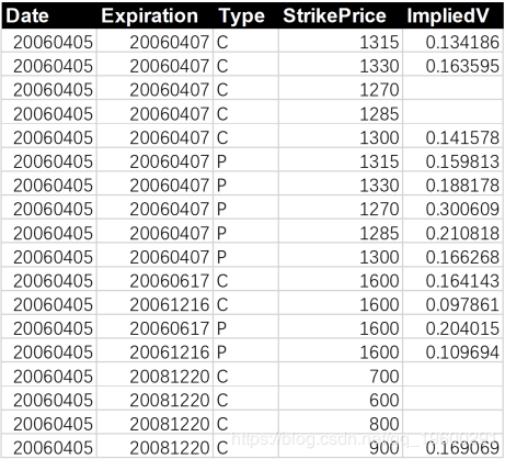我们可能会注意到一些隐含波动率数据被遗漏。这可以通过看涨期权价格的下限来解释。当标的资产具有0波动率时，期权价格达到其下限。当实际价格低于下限时，会出现负的隐含波动率，因此我们将其视为错过。
在确定要考虑哪个ATM认购期权合约时，我们选择期权合约，其中执行价格/底层价格的比率最接近1.要选择OTM认沽期权合约，我们首先筛选出合约0.9 <执行价格/底层证券价格<0.95，然后取其执行价格/基础比率最接近0.92的那个。此外，我的多个合同可能满足条件，我们只选择成熟期为30-60天的合同。期限过短的期权往往会出现更加波动的价格波动，期限过长的期权数量很少，无法反映知情交易。本文使用每周平均隐含波动率来检查，从周三到下周二。这个过程在Python中完成，如下面的代码所做的那样。
import pandas as pd
import numpy as np
#read H5S data
#pd.read_excel('SPXOption.xlsx').to_hdf('SPXOption.h5s','data')
ImpliedV=ImpliedV1.append(ImpliedV2)
del ImpliedV1,ImpliedV2
ImpliedV['Expiration']=todatetime(ImpliedV['Expiration'])
#ImpliedV=pd.read_excel("D:\USData\SPXOption.xlsx")
All_Date=pd.Series(ImpliedV.groupby('Date').groups)
SP500=pd.read_excel('D:\USData\SP500.xlsx').iloc[:,0]
Call_Data=pd.Series(0.0,index=todatetime(All_Date),name='Call_Data')
#Select given date
All_Options=ImpliedV[ImpliedV['Date']==All_Date[ii]]
All_Options.loc[:,'Maturity']=(All_Options['Expiration']-Today).dt.days
#Select maturity
#Select type & strike price
Options_Selected_C=Date_Selected_Options[Date_Selected_Options['Type']=="C"]
Options_Selected_C.sort_values(['StrikePrice'],inplace=True)
Options_Selected_P=Date_Selected_Options[Date_Selected_Options['Type']=="P"]
Options_Selected_P.loc[:,'StrikePrice']=abs(Options_Selected_P['StrikePrice']/SP500.iloc[ii]-0.92)
Put_Data[ii]=Options_Selected_P.iloc[0,4]
SP500.index=Put_Data.index
SP500=SP500.resample('W-TUE').first()
SP500=(SP500-SP500.shift(1))/SP500.shift(1)
Final_Data['Skew']=Final_Data['Put_Data']-Final_Data['Call_Data']
Final_Data.to_csv('Final_US.csv')
考虑到人们普遍承认该指数具有动量效应，我们在STATA中运行以下回归：
Index_Return [t + 3] =β_0+β_1* Volatility_skew [t] +β_2* Last6M_Index_Return [t] + e
显然，索引返回数据集具有异方差性和自相关特性。运行Newey-West回归数据来调整异方差性和自相关性。
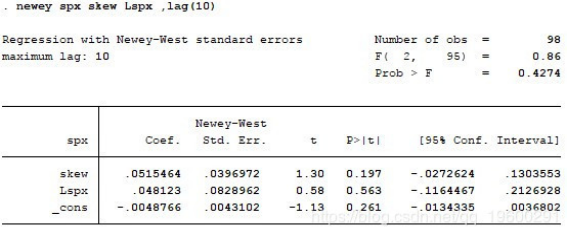从变量Volatility_skew的参数为负的结果，这成功地证明了我们的假设
中国市场
对于中国市场，我们使用SH50ETF期权，这是唯一的交易所交易期权合约。由于中国市场的动量效应与美国市场不同，我们采用尝试和误差方法 - 我们尝试将过去5,10和15个月的指数返回数据作为自变量之一。结果如下：
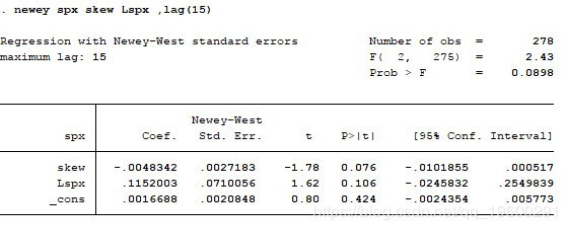
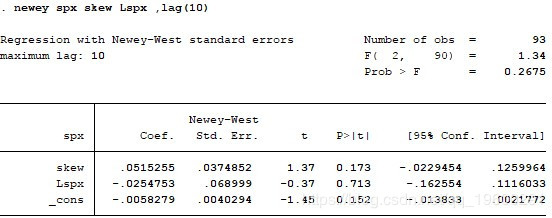
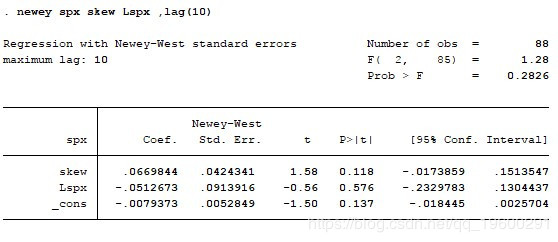但是，在中国市场，期权价格并未包含知情交易者的信息。我个人认为，由于严厉的监管以限制2015年8月股市崩盘后的未平仓合约，这一点很大。SH50ETF刚刚于2015年2月上市，在每周频率的情况下没有足够的数据供研究。
交易策略
我们使用从SPX期权波动率假笑中提取的信息制定了交易策略。当市场周二收盘时，我们计算每周平均波动率偏差，以及过去6个月的指数收益率。什么时候
β_0+β_1* Volatility_skew [t] +β_2* Last6M_Index_Return [t]> 0
我们在第三周看跌S＆P500期货。从回归我们知道β_0=0.0016688β_1=-0.0048342β_2= 0.1152003。该策略是用Python编写的：
# -*- coding: utf-8 -*-
Final_Data=pd.read_csv(r'D:\USData\Final_US.csv',index_col=0)
TestData=deepcopy(Final_Data)
Direction=pd.Series(0.0,index=range(0,len(TestData.index)))
TestData.dropna(axis=0,inplace=True)
for ii in range(0,270):
Direction[ii]=-.0048342*TestData.iloc[ii,0]+.1152003*TestData.iloc[ii,2]+.0016688
Total[ii+1]=Total[ii]*(1-TestData.iloc[ii,1])
如果我们使用此策略进行交易，这是一个净值图表
很明显，这一战略是一个成功的战略，并且在2008年的股市崩盘中也取得了成功。
