Use of PLC module to control a rotary table to cut spiral bevel gear with three-axis CNC milling

S. Mohsen Safavi & S. Saeed Mirian & Reza Abedinzadeh & Mehdi Karimian

Received: 25 November 2008 / Accepted: 23 November 2009 # Springer-Verlag London Limited 2009

Abstract

　　　CNC machining nowadays makes more use of "Mechatronics" increasingly. Combining numerical control with mechanic, electric, and data processing systems can lead to new methods of production. In recent years, the development of CNC has made it possible to perform nonlinear correction motions for the cutting of spiral bevel gears. In this paper, we attempt to manufacture the spiral bevel gear using a three-axis CNC milling machine interfaced with an additional PLC module based on traditional discontinuous multi-cutting method accomplished by using a universal milling machine interfaced with an indexing work head. This research consists of (a) geometric modeling of the spiral bevel gear, (b) simulating the traditional and our new nontraditional method using a CAD/CAE system, (c) process planning for CNC machining and PLC Programming, (d) experimental cuts with a three-axis CNC milling machine were made to discover the validity of the presented method. The results demonstrate that invented experimental cutting method of SBGs not only is less expensive than advanced CNC machining but also produces gears in a shorter time in comparison with the traditional cutting. Thereby, it is an economical method in manufacturing of SBGs.

Keywords：Gear manufacturing . Spiral bevel gear .CAD/CAM/CAE . CNC . PLC . AC motor . Inverter .Proximity sensors . Photoelectric sensors . Rotary encoder

1 Introduction

　　　Gears are important and precision mechanisms for industrial machinery as a means for mechanical power or motion transmission between parallel, intersecting and nonintersecting cross-axis shafts. Although hidden from sight, gears are one of the most important mechanical elements in our civilization. They operate at almost unlimited speeds under a wide variety of conditions. The machines and processes that have been developed for producing gears are among the most existing ingenious ones. Whether produced in large or small quantities, in cell, or job shop batches, the sequence of processes for gear manufacturing requires four sets of operations:

　　　1. Blanking

　　　2. Gear cutting

　　　3. Heat treatment

　　　4. Grinding

Depending on their type and application or required strength and resistance, gears are manufactured by casting, extruding, forging, powder metallurgy, plastic molding, gear rolling, and machining. Among these processes, machining is more frequently used for high-precise gears. Among the various types of gears, the spiral bevel gears (SBG) are the most complex type and are used to transmit the rotational motion between angularly crossed shafts.

　　　SBGs have teeth curved longitudinally along the length of the teeth. The main advantage of these gears over the straight-toothed varieties lies in the fact that more teeth are in contact at the same time because of the curve-shaped contour of the teeth and so a smoother meshing action between the mating pair is ensured. The design and manufacturing of spiral bevel gears is still a hot topic of research that is vital for application of such gears in helicopter transmissions, motorcycle gears, reducers, and in other branches of industry. As far as manufacturing is concerned, the gears are machined by a special type of machine tools, such as gear hobbing and shaping machines. Recently, special CNC-based gear manufacturing machine tools are used in industrial practice. This may be why literature on gear manufacturing is sparse in the open research domain. Recently, CNC-based gear manufacturing machine tools have been developed and increasingly used in industrial practice. However, their kinematic structure is still inherently different from the industrial CNC milling machine, as the former is designed for a special type of cutter.

　　　Previous studies on gears have been mainly concerned with the design and analysis of gears. The geometric characteristics and design parameters of gears have been studied. Tsai and Chin presented a mathematical surface model for bevel gears (straight and SBGs) based on basic gearing kinematcis and involute geometry along the tangent planes. Later, this method was compared with another model based on exact spherical involute curves by Al-daccak et al. Shunmugan et al. presented a different model, and its accuracy (compared with the spiral bevel gear manufactured by special machine tools) was verified in terms of nominal deviation.

　　　For crown gears, a few results are available. Litvin and Kim suggested a generation method for an involute curve from a modified base circle for a spur gear. Umeyama designed a standard profile at the pitch circle and a modified profile at the top/bottom face gear with a determination of the modification value for transmission error of helical gear. Tamura et al. studied a point contact model for a bevel gear using a flat surface tooth. These studies are concerned with the generation of the tooth profile for special gear machines, such as gear hobbing and shaping machines, which are specially designed for manufacturing gears. Suh et al. investigated the possibility of a sculptured surface-machining method for the manufacture of spiral bevel gears and verified the possibility by presenting tool-path generation using a four-axis CNC milling machine interfaced with a rotary-tilt table. A model-based inspection method for the spiral bevel gears was also presented.

　　　In this paper, we attempt to present a new manufacturing procedure of SBGs by using a three-axis milling machine interfaced with a PLC module which operates as an indexing table. In terms of production rate, it is obvious that this method will be lower than that of the special machine tool. Other than production rate, this method is advantageous in the following respects: (1) the conventional method requires a large investment for obtaining various kinds of special machinery and cutters dedicated to a very limited class of gears in terms of gear type, size, and geometry; (2) by this method, various types of gears can be manufactured with the industrial three-axis CNC milling machine; (3) this method is more economical than using the special machine tool. One of the main points which separate our work from previous ones is developing an automatic computer model in order to simulate the process entirely and obtain machining parameter. All previous studies have been engaged in calculating complicated mathematical equations and designing geometric models. In view of the above, special attention is given to experimental tests rather than presenting geometrical or mathematical model of SBGs. This is the first time that mechatronic tools and a three-axis CNC milling machine are being used simultaneously in manufacturing a special gear and even a mechanical element.

2 Geometric specifications of the spiral bevel gears

　　　Most of the time, the geometric parameters of a gear are provided with an engineering drawing. Some parameters (principal parameters) are required for defining the geometry. To calculate these parameters, we have used “drive component development software” called GearTrax.

　　　The design of spiral bevel gear requires high-accuracy mathematical calculations, and the generation of such gear drives requires not only high-quality equipment and tools for manufacturing of such gear drives but also the development of the proper machine-tool settings. Such settings are not standardized but have to be determined for each case of design (depending on geometric parameters of the gear drive and generating tools) to guarantee the required quality of the gear drives.

3 Manufacturing the SBG

　　　As it was discussed in the introduction, by machining, all types of gears can be made in all sizes, and machining is still unsurpassed for gears having very high accuracy. Form milling is one of the most common machining processes used to manufacture any types of gears. The cutter has the same form as the space between adjacent teeth. Standard cutters usually are employed in form-cutting gears. In the USA, these cutters come in eight sizes for each diametral pitch and will cut gears having the number of teeth indicated in standard tables. Gleason works used the face hobbing process that is based on the generalized concept of bevel gear generation in which the mating gear and pinion can be considered respectively, generated by the complementary generating crown gears.

　　　As it is shown in Eq. 1, velocity ratio of face hobbing process depends on tooth number of tool and generating gear:

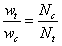                                       （1）

where, wt and wc denote the angular velocities of the tool and generating gear; Nt and Nc denote the number of the blade groups and the tooth number of the generating gear.

　　　The radii of the rolling circles of the generating gear and the tool are determined by Eqs. 2 and 3:

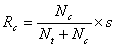　　　　　　　　　　　　　　　　                       （2）

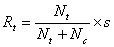　　　　　　　　　　　　　　　                         （3）

where s is the machine radial setting.

　　　The generating crown gear can be considered as a special case of a bevel gear with 90° pitch angle. Therefore, a generic term “generating gear” is used. The concept of complementary generating crown gear is considered when the generated mating tooth surfaces of the pinion and the gear are conjugate. In practice, in order to introduce mismatch of the mating tooth surfaces, the generating gears for the pinion and the gear may not be complementarily identical. The rotation of the generating gear is represented by the rotation of the cradle on a hypoid gear generator.

　　　To manufacture the SBGs with the three-axis CNC milling machine, we first test the process by developing a CAD/CAM system composed of geometric modeling and graphic simulation modules. The commercial software Solidworks is used for creating CAD model and MSC. Visual NASTRAN 4D (CAE system of the kinematic analysis of the mechanisms by means of their 3D models) is used for simulating the process of gear manufacturing and its analytical results.

　　As far as machine tool configuration is concerned, it is obvious that a rotational motion of the workpiece is required for NC machining of the SBGs. Based on the machinability analysis, at least four-axis controls are required for NC machining of SBGs by one setup. Thus, a rotary table to be interfaced with the three-axis milling machine is required. Form cutting or form milling is used in our tests. The tool is fed radially toward the center of the gear blank to the desired tooth depth, then across the tooth face, while the rotary table rotates the workpiece around its center to obtain the required tooth width. When one tooth space has been completed, the tool is withdrawn, the gear blank is indexed using a dividing head, and the next tooth space is cut. Basically, this method is a simple and flexible method of machining SBGs. The equipment and cutters required are relatively simple, and standard three-axis CNC milling machine is used. However, considerable care is required on the part of tool feed which should be a small value in each step to prevent any spoil.

　　　We used spiral bevel gear created in GearTrax in order to simulate operating sequence and then estimate some machining parameters such as initial height of end mill, location of proximity sensors, motor torque, motor speed, and rotation frequency. For example, in SolidWorks, distance between end mill and the apex of SBG was 14.7 mm which we used to locate the spindle vertically along the z-axis.

　　　Also, according to the graph report of CAE system which we used, motor angular velocity and motor torque are 1 rpm and 48 Nm, respectively.

　　　Mastercam is a mechanical software that can be used to generate toolpaths for machining. According to whole depth and face width of the gear, a rectangular contour was designed as toolpath in our cutting procedure.

　　　Other machining parameters and tool’s specifications were also submitted to the Tool Path menu of software. In contour window, there are two options which we use:

　　　1. Multipasses which enable multiple stepovers of the tool, allowing for greater control of stock removal.

　　 2. Lead in/out which extend or shorten the toolpath before making entry/exit moves without creating additional geometry, which is helpful when working with control compensation and makes it possible to program solid contours in less time.

　　　Although the form cutting of this kind of gears is currently done on universal milling machine, using an indexing head, the process is slow and requires skilled labor and operator. The cutter is mounted on an arbor, and a dividing head is used to revolve (required to cut the gear tooth) and index the gear blank. The table is set at an angle equals to the spiral angle (35°), and the dividing head is geared to the longitudinal feed screw of the table so that the gear blank will rotate as it moves longitudinally.

　　　In the presented method, we have used an alternating current (AC) motor interfaced with a worm gearbox. Worm gearbox is used to reduce the output speed of AC motor and also to set the angle between the tooth trace and the element of the pitch cone, known as spiral angle.

　　　Since synchronization between tool path planning and rotary motion of outward shaft of worm gearbox is required, a mechatronics system to control all the four axes (one-axis motion for the rotary table and three-axis motion for the cutting tool) was used simultaneously.

　　　At the same time we used ladder diagram, common program language to operate the PLC in the mechatronics system.

　　　The operation of the PLC based on the ladder diagram is as follows:

　　　Step 1 Read the external input signal, such as the status of sensors or rotary encoder.

　　　Step 2 Calculate output signal, according to the value of the input signal in step 1 and send it to AC drive (Inverter) to run the AC motor in forward/reverse direction or turn the motor for a special angle (circular pitch) using a rotary encoder. Having set up the CNC milling machine, the procedure of the whole system is accomplished in five stages:

　　　Stage 1 Form cutter reaches the first proximity sensor. As soon as sensor 1 detects the form cutter, it sends a +5-V signal to the PLC. As it is mentioned before, PLC sends out an output signal to the AC drive to run the motor in forward direction.

　　　Stage 2 Form cutter machines the rotating workpiece with respect to the toolpath has been generated in Mastercam.

　　　Stage 3 Cutting tool reaches the second proximity sensor. Detecting form cutter by sensor 2, it sends the second signal to the PLC and PLC sends a stop command to the inverter.

　　　Stage 4 Milling tool withdraws the stopped workpiece and returns to its first place. Simultaneously, AC drive runs the motor in backward direction until the shaft reaches the first position which the receiver of photoelectric sensor sees the transmitted radiation passes through the longitudinal crack on the output shaft.

　　　Stage 5 Stages 1 through 4 continue until the first tooth space is cut. PLC counts a number for each of the above four stages until it reaches the predefined number of machining sequences. Then, it sends out a signal to the AC drive to index the gear blank equal to diametral pitch, and all the above stages will be repeated again. The diametral pitch is measured by a 1,024-pulse/revolution rotary encoder.

　　　In an advantageous embodiment of the method according to the present invention, machining time is one of the most factors which have been greatly noted. For example, it took only 2 min to cut one tooth space completely. While, in traditional method, it took more than half an hour to cut same tooth space.

　　　In a further advantageous embodiment of the present invention with respect to manual cutting, the instant for the angular compensation of the cutter head is set shortly before the end of the plunge process.

4 Machining strategy

　　　The workpiece is wood, and the blank material is premachined as a conic (face angle of the gear) form by turning operation. Standard cutter No. 5 used in our experiment is mounted on the machine spindle, and the gear blank is mounted on outward shaft of worm gearbox. The tool is fed subsequently (around 30 machining sequences to prevent spoiling work) toward the center of the gear blank to the desired tooth depth. When one tooth space has been completed, the tool is withdrawn; the gear blank is indexed using the AC motor based on explained procedure and then is followed by cutting the next tooth space.

5 Conclusions

　　　In this paper, we attempted to manufacture the spiral bevel gear using a three-axis CNC milling machine based on form milling method. For such a purpose, we investigated a CAD/CAM model of cutting procedure and also tool path computing algorithm. All previous works have been concerned with the design aspect using complicated mathematical procedure, and experimental manufacturing methods have not been explicitly focused. Basically, form cutting uses a simple and flexible method of machining of gears. The equipment and cutters required are relatively simple and inexpensive, and standard CNC milling machine is used. So, it does not need skilled operator to set up the system. Compared to the conventional gear cutting

method in which dedicated machine tools is required, the presented method can easily be modified to produce any type and size of SBGs or any other types of gears. In comparison to manual cutting machine, it is a complete automatic method in which all machining parameters are derived from the computer model. It is also a multideception system (use of mechatronic and CNC systems) which is a dynamic and constant evolving technology.

References

1. De Garmo EP, Black JT (1957) Materials and processes in manufacturing. Prentice–Hall, New York

2. Shigley JE (1986) Mechanical engineering design. McGraw-Hill, New York

3. Maitra GM(1994)Handbook of gear design. McGraw-Hill, New York

4. Tsai Y, Chin P (1987) Surface geometry of straight and spiral bevel gears. ASME J Mech Trans Autom Des 109(4):443–449

5. Al-daccak M, Angeles J, Gonzalez-Palacios M (1994) The modeling of bevel gears using the exact spherical involute. ASME J Mech Des 116:364–368

6. Shunmugam M, Narayana S, Jayapraksh V (1998) Establishing gear tooth surface geometry and normal deviation: part 1— cylindrical gears. J Mech Mach Theory 33(5):517–524

7. Shunmugam M, Rao B, Jayaprakash V (1998) Establishing gear tooth surface geometry and normal deviation: part 2—bevel gears. J Mech Mach Theory 33(5):525–534

8. Litvin F, Kim D (1997) Generation and simulation of meshing of modified involute spur gears with localized bearing contact and reduced level of transmission errors. ASME JMech Des 119:96–100

9. Umeyama M (1995) Effects of tooth surface modifications on the transmission error of a helical gear pair and its opimization. Trans Jpn Soc Mech Eng C 61(582):8–15

10. Tamura H, Tanaka K (1992) A method of cutting spiral bevel gears using a quasi-complementary crown gears. Trans Jpn Soc Mech Eng C 58(547):202–208

11. Tamura H et al (1997) Method for cutting straight bevel gears using a quasi-complementary crown gears. Trans Jpn Soc Mech Eng C 63(606):259–264

12. Suh S, Ji W, Chung D (2001) Sculptured surface machining of spiral bevel gears with CNC milling machine. Int J Mach Tools Manuf 41:833–850

13. Suh S, Lee E, Kim H (2002) Geometric error measurement of spiral bevel gears using a virtual gear model for STEP-NC. Int J Mach Tools Manuf 42:335–342

14. Krenzer TJ (1990) Face-milling or face hobbing, AGMA. technical paper, 90 FTM 13

15. Pitts LS, Boch MJ (1997) Design and development of bevel and hypoid gears using the face hobbing method. Cat. No. 4332, The Gleason Works

16. Suh S, Kang J (1995) Process planning for multi-axis NC machining of free surfaces. Int J Prod Res 33:2723–2738

17. Dudley DW (1962) Dudley’s gear handbook. The design, manufacture and application of gears. McGraw-Hill, New York

18. Jaeschke R (1978) Controlling power transmission systems. Penton/IPC, Cleveland, pp 210–215

19. Campbell S (1987) Solid-state AC motor controls. Marcel Dekker, New York, pp 79–189 ISBN 0-8247-7728-X