摘要
支持向量机是Vapnik等人基于统计学习理论提出的一种新型机器学习方法。由于采用了结构风险最小化原则替代经验风险最小化原则,使它能较好地解决小样本学习问题。又由于采用了核函数思想,使它能把非线性问题转化为线性问题来解决并降低了算法的复杂度,而且它具有很好的通用性,鲁棒性,有效性,计算简单等特点,所以支持向量机己被广泛应用于人脸识别,手写识别,模式分类等领域。但是作为一种新兴技术,支持向量机在很多应用领域的研究还有待探索和完善。支持向量机的训练算法在对大规模的数据集进行训练时,训练时间往往过长、算法复杂而难以实现。
本文主要对支持向量机训练算法进行了探讨。首先对支持向量机的基本理论进行了介绍。然后对支持向量机的集中训练算法进行了一般描述。接下来重点介绍了一种比较成功的算法:SMO算法。这种算法都很大地提高了大规模训练集的训练速度。本文的主要工作有:
(1)系统地论述了支持向量机的理论基础,包括统计学习理论基础和支持向量机理论基础。
(2)对支持向量机的训练算法做系统的介绍。
(3)着重介绍了SVM训练算法中比较成功的SMO算法做详细的描述,尤其是算法的推导过程。
关键词:支持向量机;统计学习理论;最优超平面;核函数;二次规划;SMO
ABSTRACT
Support Vector Machine (SVM) is a new method of Machine Learning which is proposed by Vapnik and his group based on the statistical learning theory. It can solve small samples learning problems better by using structural risk minimization in place of experiential risk minimization. Because SVM adopts the thought of kernel function, it can change the nonlinear problems into linear problems to reduce the complexity of algorithm. It also has some advantages in the generality, robustness, effectiveness, simple calculation. So it has been widely used in face recognition, handwriting recognition, pattern classification and other fields.But as a new technique,SVM also have many shortcomings that need to be researched, such as: it costs too much time when training large-scale data set and its alogrithm is so difficult to implentmenion.
In this paper, we main discuss the training alogrithm of SVM. At first, this paper introduced the basic concept of SVM theory. Then we gived a general description of the training alogrithm of SVM. As following, we paid main attention to the successful training alogrithms一SMO. The SMO alogrithm improved the trianing speed on large-scale training set greatly.
The main work of this article:
(1)Systematically described the basic concept of SVM theory,including Statistical learning theory and Support vector machine theory.
(2)Systematically introduced the training alogrithm of SVM.
(3)Detailed introduction of SMO algorithm which is one of the successful SVM training algorithm, especially for the alogrithm derivation.
Keywords:Support vector machine; statistical learning theory; optimal hyperplane; nuclear function; quadratic programming; SMO
目 录
1. 绪论 1
1.1支持向量机的研究背景、意义 1
1.2 SVM算法研究现状 2
1.3 论文内容及结构安排 4
2. 统计学习理论基础 4
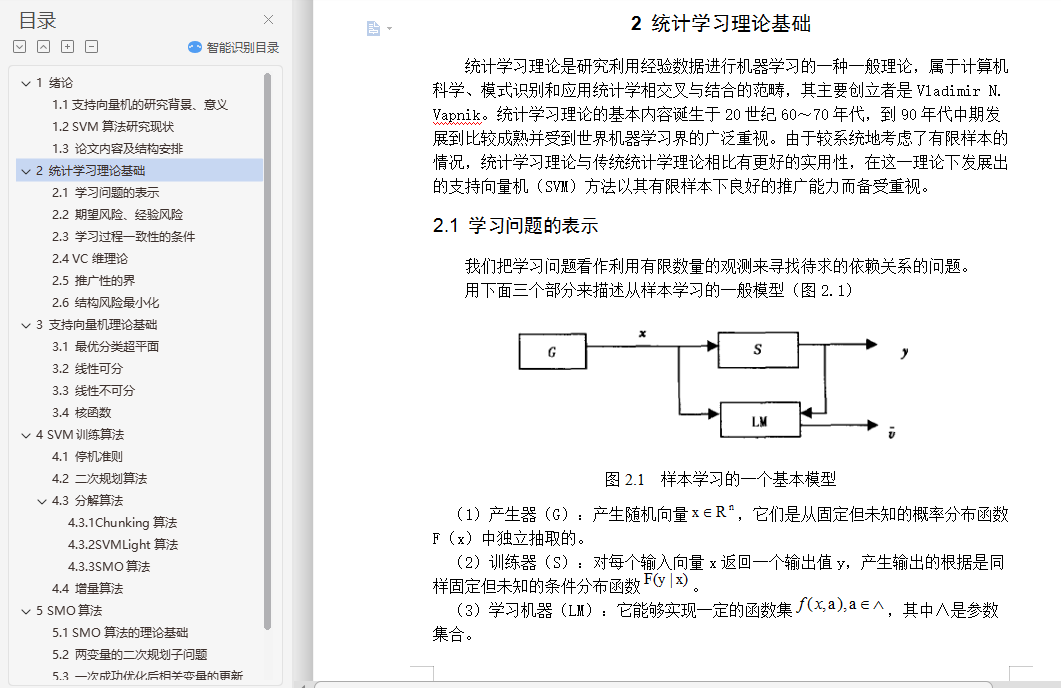
2.1 学习问题的表示 4
2.2 期望风险、经验风险 5
2.3 学习过程一致性的条件 6
2.4 VC维理论 7
2.5 推广性的界 9
2.6 结构风险最小化 11
3. 支持向量机理论基础 13
3.1 最优分类超平面 13
3.2 线性可分 14
3.3 线性不可分 16
3.4 核函数 17
4. SVM训练算法 18
4.1 停机准则 19
4.2 二次规划算法 21
4.3 分解算法 23
4.3.1Chunking算法 23
4.3.2SVMLight算法 24
4.3.3SMO算法 26
4.4 增量算法 27
5. SMO算法 28
5.1 SMO算法的理论基础 28
5.2 两变量的二次规划子问题 30
5.3 一次成功优化后相关变量的更新 34
5.4 待优化变量的选择及smo算法步骤 36