摘要
材料性能及其在高温下的变化是结构防火中的关键部分,在高温下与结构碳钢相比,不锈钢显示出优越的强度和刚度的保持能力。尽管同样重要的是高温下强度和刚度的广西对结构部件的弯曲反应也有重要的影响。本文以现有的试验成果,利用ABAQUS提出了一个数值参数研究。此试验估算了对局部和整体的初始几何缺陷,冷作用条件下角部强度的增强,以及对柱膜端的局部保护。参数研究探讨了截面大小变化和荷载水平的影响。试验结果与现行的设计规则进行了比较。分析了23个钢柱燃烧试验,6个短柱燃烧试验和6个梁燃烧试验的结果,最突出的是过于保守的试验结果,对弯曲现象中处理的不一致性,以及对变形极限的选择。提出修定的不锈钢在火中弯曲曲线一贯的应变,一个截面分类的新办法及对局部弯曲的处理,这些修改使得对于不锈钢梁、柱在火中的弯曲的处理更加一致和有效,与现行的Eurocode方法相比较,不锈钢抗弯曲能力提高36%,残柱的抗力提高38%,平面抗弯曲能力提高14%。
关键词:梁,屈曲,高温,火灾,不锈钢,结构
1.前言
结构中具有首要重要性的是在火灾爆发的突发情况下,保持结构的承载能力,防止在居民、消防人员工作前发生过早的倒塌。金属结构相对于木材或钢筋混凝土结构来说通常更容易受到火灾的影响,这是因为结构构件的相对快的温度变化,这主要是由于其高的表面积和体积之比,以及材料的高导热性,相对低的火灾发生率反映在减少局部安全因素的使用上。主体钢结构在火灾中日益受到重视,关于钢结构在高温下的行为和对于防火安全设计时的指导的背景信息可在[1,2]中找到,最近对于这个方面的理解取得了新的发展,特别是90年代中期完成的对全面的Cardington火灾试验的观察和分析。例如,结构连续性的重要意义已经被广泛接受。但对于钢结构在火灾中的应用注意力不够,主要是由于目前不锈钢在结构工程中的应用相对有限,然而不锈钢在结构及建筑方面的应用正在有所增长,一部分是由于这种材料有吸引力的外观,较高的耐腐蚀性能,维护方便,低的生命周期成本和耐火性,同时拥有改进了的更广泛的设计指导以及提高了的产品可用性。
在高温下,与结构碳钢相比,不锈钢拥有优越的强度和刚度保持能力,这归功于合金元素有利的影响,这种行为反映在EN1993-1-2(2005)[8]里,正如图1和图2显示的那样,图1显示的强度减小量是1.4301等级奥氏体不锈钢的,它是结构应用中使用的最广泛的钢种,然而图2显示的刚度减少由于是所有等级普遍符合的,强度减小因数可根据两种应变水平来定义: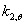 是2%全应变
是2%全应变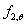 下的高温强度,由室温0.2%屈服强度
下的高温强度,由室温0.2%屈服强度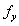
标准化,而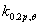 是高温0.2%屈服强度
是高温0.2%屈服强度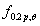 ,由室温0.2%屈服强度标准化。刚度减小因素
,由室温0.2%屈服强度标准化。刚度减小因素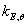 被定义为高温初始
被定义为高温初始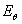 ,由室温下初始切线模量
,由室温下初始切线模量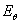 标准化,其他的热力学性能,包括那些影响温度变化的因数都在[9]中讨论,值得一提的是在指定的最底室温下,常见的奥氏体不锈钢的强度通常介于210
标准化,其他的热力学性能,包括那些影响温度变化的因数都在[9]中讨论,值得一提的是在指定的最底室温下,常见的奥氏体不锈钢的强度通常介于210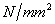 到240
到240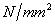 之间,而杨氏模量为200000
之间,而杨氏模量为200000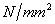 。
。
详见第五部分,除了高温下材料强度和刚度的下降,强度和刚度两者之间的关系也同样重要,因为这反映了对弯曲的敏感性。对于结构不锈钢设计,这个概念包括在构件弯曲中,尽管不是局部的平面弯曲。这就是此处提出的不一致性。
2.结构不锈钢构件燃烧试验回顾
关于不锈钢结构构件在火中的反应的一系列试验研究已经实行,本节总结了所有这些测试的结果,随后用来与现存的设计方法做比较,并用以修正设计准则。这些测试已有选择地复制在本文的第3节,构成了参数研究的基础。
对于共23个奥氏体不锈钢柱,6个残柱,6个不锈钢深梁的燃烧试验结果已公布,表格1-3提供了这些测试的摘要。名义截面尺寸,横截面分类,边界条件实用载荷和临界温度已列。表格1中标记“a”或“b”的已详细报告,并用来证实数值模型。如下部分所述。在表格1中描述的23个钢柱弯曲测试中,4个有固定的边界条件,其余的为pin-ended。所有测试都在空心截面上进行(19个矩形空心截面,3个圆形空心截面),除了一个I-截面外,它是一对槽钢背以焊接而成。表格2中的6个短柱试验中都是矩形空心截面,表格3中的6个梁试验包括1个矩形空心截面,3个I-截面和2个top-hat截面。所有测试梁都有一个具体的平板提供充分的横向约束。没有关于不受约束的不锈钢梁的防火测试。所有的测试都是非等温的,栽荷维持在一个固定水平,温度则是上升的直到破裂。
3.数值模型
3.1 概况
数值模型研究是为了更好的了解不锈钢部件在火中的屈曲反应及研究关键参数的影响。研究中应用了有限元软件ABAQUS。分析模拟了12个钢柱的屈曲火灾试验(如图1所示)
随后做的灵敏性研究是为了弄清局部和整体初始几何缺陷的影响以及冷作条件下角部材料的性能。参数研究用来评估局部横截面细度的变化,全体构件细度以及载荷水平不锈钢构件用壳单S4R来模拟,其中有4个角落节点,每个有6个自由度,适用于厚壳或薄壳,网格会聚研究是用来确定一个适当的网格密度以得到精确的结果,同时保持实际计算次数。横截面宽度上网格尺寸为2至10个单元的模型部有类似的结果板宽上有5个单元,网格长度方向上的尺寸采用最佳比例。
本文第2部分中讨论的火灾试验是非等温进行的,这反映在数值模拟中分为两个步骤来分析:第一步,载荷在室温下施加于柱上,第二步,温度依照测得的温度一时间关系逐渐增加,值得一提的是,RHS40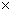 40
40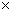 4试验并没有遵守ISO834-1标准,取而代之的是,采用了温度和时间的双线性关系,这个关系也包括在采用测定温度-时间数据的数值研究中。
4试验并没有遵守ISO834-1标准,取而代之的是,采用了温度和时间的双线性关系,这个关系也包括在采用测定温度-时间数据的数值研究中。
3.2 材料模拟
材料模拟是有限元模拟中的重要方面之一。不适当的材料行为定义将极大地阻碍模型复制观察到的结构反应的能力。在目前的研究中,材料模型是建立在符合测定的高温应力-应变数据的双线性关系基础上的,实测的Ala-Outinen和Oksanen的应力应变曲线是相当不稳定的,尤其在小应变下,有些区域承应变增加硬度也上升。因此为了得到平稳的应力-应变关系,Ramberg-Osgood模型的够精确地描述出测定的应力-应变数据图3显示了在200℃和600℃下用Ramberg-Osgood formulation测得的应力应变曲线。
ABAQUS要求材料应力-应变关系是根据真实应力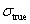 和塑性应变对数
和塑性应变对数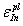 来定义的,而Eqs.(1)和(2)中,
来定义的,而Eqs.(1)和(2)中,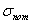 和
和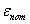 分别是工程应力和工和应变,E是杨氏模量所有模的材料热膨胀系数取自EN 1993-1-2[8]。
分别是工程应力和工和应变,E是杨氏模量所有模的材料热膨胀系数取自EN 1993-1-2[8]。
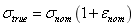 (1)
(1)
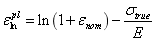 (2)
(2)
3.3 角部材料性能
不锈钢的机械性能对冷作水平很敏感,导致角部区域的0.2%屈服强度应高于平滑区域的。数值模拟中若未能加强这些区域强度,将会导致承载能力被低估或在现行研究中耐火性被低估。甚于取自冷作不锈钢角部区域的材料所做的拉伸试验,角部材料强度的预测值有所上升。有人提议,轧制成型和成型过程中材料的0.2%屈服强度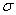 0.2c都可用(3)式计算。
0.2c都可用(3)式计算。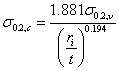 (3)
(3)
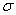 0.2v是材料加工前0.2%屈服强度,
0.2v是材料加工前0.2%屈服强度,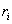 是角部内半径,
是角部内半径,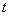 是材料厚度。(3)式已在现行研究中被用来预测press-backed截面的角部性能。
是材料厚度。(3)式已在现行研究中被用来预测press-backed截面的角部性能。
还有人提出角部材料的极限强度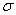 u,c可在它的0.2%屈服强度基础上估算,而
u,c可在它的0.2%屈服强度基础上估算,而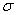 0.2c,
0.2c,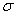 0.2v,
0.2v,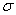 u,v都由
u,v都由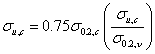 (4)式给出。(4)式此处用来估算角部材料的极限强度
(4)式给出。(4)式此处用来估算角部材料的极限强度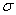 u,c。试验结果显示冷作下材料强度和硬度的退化大体上与退火材料相似。
u,c。试验结果显示冷作下材料强度和硬度的退化大体上与退火材料相似。
强度增强最多可保持到800℃,超过它后就消失了,因此,角部在高温下的应力应变性能是建立在设定室温下角部性能和测定的强度和硬度减小因子基础上的,除了由于冷作产生的角部强度增加外,延伸出弯曲角的区域的强度增加程度也是很重要的。室温下数值研究已显示,press-backed部分的角部强度增加现象一直延伸至角部外相当于材料厚度的距离内,而在轧制成型部分这个延伸距离为厚度2倍。目前的研究中,模型灵敏性研究建立在4个SCI柱试验基础上的,为了估算出不锈钢柱强度区域的范围对耐火能力的影响表格4显示了模型钢柱的平直材料的0.2%屈服强度的测量值和角部材料强度的计算值,总结了灵敏性研究的结果。
有限元模型有三种:(1)没有角部强度增强现象(FE),(2)角部强度增强现象仅发生在弯曲角部分,(3)角部强度增强现象延伸至弯曲角外相当于材料厚度大小的距离内(FE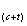 )模型包括了全局缺陷幅度L/1000,L是柱长。结果大体上是显示出随着强度区域的增大,对于测试行为的预测值有显著提高,对耐火能力的高估是由于测试样本的不佳表现,而不是模型缺陷。角度强度增强的重要性将取决于截面的几何形状,尤其是角部面积与总横截面积的比值。然而,表格4中的比较显示不考虑角部强度增强将会导致它的耐火能力降低大约5%~10%。
)模型包括了全局缺陷幅度L/1000,L是柱长。结果大体上是显示出随着强度区域的增大,对于测试行为的预测值有显著提高,对耐火能力的高估是由于测试样本的不佳表现,而不是模型缺陷。角度强度增强的重要性将取决于截面的几何形状,尤其是角部面积与总横截面积的比值。然而,表格4中的比较显示不考虑角部强度增强将会导致它的耐火能力降低大约5%~10%。
3.4 残余应力
残余应力对结构部件的影响是引起横截面某部分过早屈服,因此减少硬度对于冷作截面,残余应力主要是在塑性变形过程中产生的。然而,[20,24]研究得出结论,结果材料特性是建立券剪下来的横截面。这些弯曲残余应力的影响将先天存在,不需要在有限元模型中明确定义。
在一项由Gardner和Nethercot做的研究报告中,估算了不锈钢残柱模型对表层残余应力的敏感性。有限元模拟其它参数相同条件下,分别进行了有无残余应力的模拟试验。结果显示残余应力引起残柱硬度的下降,但是对它们的整体变化或最终承载能力无太大影响。[25]也得出相似的结论,在高变形高温下,残余应力影响可忽略不计,因此在现行研究中被忽略。
3.5几何缺陷
所有的结构构件包含几何缺陷,会对结构行为产生重要的影响。全局缺陷和局部缺陷都包括进现在的研究中,Gardner和Nethercot做了一系列室温下有着不同缺陷大小的不锈钢钢柱模型,缺陷幅度分别是L/1000,L/2000,L/15000,L是柱长。比较显示整体缺陷幅度为L/2000的有限元模拟结果和实测结果最为吻合。在现行的高温研究中,考虑了三种缺陷形式,L/2000 ,L/1000和L/500,被用于数值模型中结果如表格与所示。在整体缺陷敏感性研究中,仅仅在弯曲角部分强度增强,比较显示,对于室温下柱体弯曲整体缺陷为L/2000的,与高温下试验结果有较好的一致性。因此,全局缺陷为L/2000的继续用以剩下的研究中。
局部缺陷也包括在模型中,为了确保局部平面弯曲不受抑制。在接下来对不锈钢空心部分缺陷的分析中,重新校正了Dawson和Walker提出的模型,从而给出了
(5)式可预测局部缺陷幅度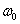 。
。 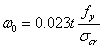 (5)
(5)
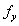 是材料0.2%屈服强度,
是材料0.2%屈服强度,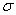 cr是弹性临界平面弯曲应力,
cr是弹性临界平面弯曲应力,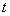 是材料厚度。
是材料厚度。
通过三种缺陷大小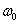 ,0.01
,0.01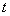 ,0.1
,0.1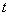 和(5)式贯穿于剩下的研究中。
和(5)式贯穿于剩下的研究中。
3.6柱体端部的保护
4个柱体,RHS150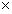 100
100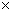 6,RHS150
6,RHS150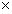 75
75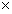 6,RHS100
6,RHS100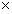 75
75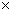 6和RHS200
6和RHS200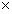 150
150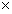 6,由一层从末端延伸至距每根柱末端200
6,由一层从末端延伸至距每根柱末端200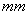 的矿物纤维保护,3
的矿物纤维保护,3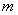 长暴露在外,如图所示。估算了这种局部保护对柱体耐火能力的影响。每一步是在热量仅施加于裸露部分情况下进行热传导分析,热量传递至保护端热传导分析结果收等温非线性分析来决定高温下柱体反应,势力学性能如EN 1991-1-2[2]和EN 1993-1-2[8]所言。
长暴露在外,如图所示。估算了这种局部保护对柱体耐火能力的影响。每一步是在热量仅施加于裸露部分情况下进行热传导分析,热量传递至保护端热传导分析结果收等温非线性分析来决定高温下柱体反应,势力学性能如EN 1991-1-2[2]和EN 1993-1-2[8]所言。
表6比较了有无端部保护的两种有限元模拟的结果,模型包括延伸至弯曲角外相当于材料厚度距离的强度增强区,整体缺陷幅度为L/2000,结果末端保护的作用是使耐火能力有微小上升。(大约平均4%)研究中采用开端保护的柱体有固定的边界条件;这样的柱体可以从末端保护中获取更多的好处。
3.7 参数研究
运用非线性有限元包ABAQUS对12个柱体进行了模拟。表7给出了试验和有限元模拟结果的比较。大体上,有限元模拟的结果和实测结果得到了较好的吻合。有限元模拟低估测试样品的耐火能力趋势,也许主要是由于恒温假设,此温度在测试样品表面上测得(即上限)。 背对背槽钢的有限元模拟优于测试,如前所述,这是由于测试样本的不准表现,而不是模型的不足。从有限元模拟与实测的结果比较中,可得有限元模型能够再现出不锈钢柱在火中的反应。
紧随着测试与有限元结果的吻合,又进行了一系列的参数研究,为了研究出不锈钢构件在高温下的弯曲反应。参数研究基于对RHS150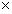 75
75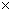 6截面的测试,采用了测定的材料性能。
6截面的测试,采用了测定的材料性能。
参数研究是为了探求横截面大小的变化,构件细度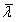 和载荷比,而载荷比是根据EN 1993-1-2[8]定的。
和载荷比,而载荷比是根据EN 1993-1-2[8]定的。
横截面变化量是考虑了一系列横截面厚度而得到的。表6显示了参数研究的结果考虑了4种横截面厚度,括号中给出了相应的横截面分类:8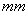 (一级),6
(一级),6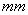 (二级)4
(二级)4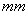 (三级)和2
(三级)和2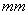 (四级)。负荷比也在0.2至0.8中变化。详见图6,结果显示了所有的1-3级截面行为相似,大体上遵循Eurocode3设计曲线。然而,对于4级截面,吻合度较差。原因有两方面。首先,负荷比是通过所施加载有的室温抗弯力的标准化而得对于第四等级截面,室温抗弯力的计算是基于局部截面弯曲的,这导致高负荷比。其次,EN 1993-1-2样本中第四等级采用的是与0.2%屈服应力一致的强度减小因子
(四级)。负荷比也在0.2至0.8中变化。详见图6,结果显示了所有的1-3级截面行为相似,大体上遵循Eurocode3设计曲线。然而,对于4级截面,吻合度较差。原因有两方面。首先,负荷比是通过所施加载有的室温抗弯力的标准化而得对于第四等级截面,室温抗弯力的计算是基于局部截面弯曲的,这导致高负荷比。其次,EN 1993-1-2样本中第四等级采用的是与0.2%屈服应力一致的强度减小因子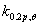 ,而1-3等级截面采用稍高的应变极限使用了
,而1-3等级截面采用稍高的应变极限使用了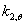 。本文第4和第5部分详述了这些测试结果的比较,及第四级截面结果吻合度的提高。
。本文第4和第5部分详述了这些测试结果的比较,及第四级截面结果吻合度的提高。
构件截面变化是通过考虑一系列柱长而得,表7显示了研究结果。正如期望的那样,一般趋势表明随负荷比上升临界温度减小,结果同样表明临界温度随负荷比的变化量与截面粗细有关。由于截面粗的柱体主要受强度衰减的控制,而截面细的柱体主要受材料硬度及其衰减的控制,而强度和硬度并不随温度认同一速率衰减,因此柱体的临界温度是取决于截面粗细的。
3.8 讨论
本部分描述了对火中的结构不锈钢部件数值研究。数值再现了12个柱体弯曲测试的结果并进行了一系列灵敏性和参数研究,是为了弄清关键的独立参数所产生的影响。主要的发现如下:
 不锈钢构件在火中的非线性现象可被精确地数值再现。
不锈钢构件在火中的非线性现象可被精确地数值再现。
 对几何缺陷和残余应力的敏感度较低。
对几何缺陷和残余应力的敏感度较低。
 角部强度增强可使临界温度提高约5%。
角部强度增强可使临界温度提高约5%。
 临界温度值依赖于截面粗细(在一给定的负荷比下)。
临界温度值依赖于截面粗细(在一给定的负荷比下)。
 第四级模型实行的远比Eurocode3预测的要好。
第四级模型实行的远比Eurocode3预测的要好。
下文中,对不锈钢耐火测试结果和现行的设计准则进行了比较,以试验结果为基础,再加上数值研究中的发现以及对结构部件弯曲行为的考虑。提出了对现行设计准则的修改。
4. 与现行设计准则的比较
本部分叙述了测试结果与现行设计准则的比较情况。在比较中,采用了测定的几何和材料性能,所有的局部因素等同为整体的。以便进行直接的比较,由Eurocode3设计准则计算出的耐火力与[12]中给出的稍有不同,这是由于新的有效的宽度公式及测定的强度值的使用,最终强度用来确定2%应变下的强度减小因子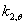 。
。
4.1压缩部件
4.1.1 Eurocode3.1,2部分
在EN1993-1-2[2005]中,在某一温度下一个压缩部件的设计弯曲应力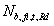 ,1-3级截面的可由(6)式确定,4级截面的由(7)式确定:
,1-3级截面的可由(6)式确定,4级截面的由(7)式确定:
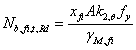 (6)
(6) 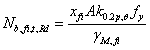 (7)
(7)
其中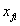 由下式求得:
由下式求得:
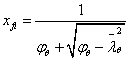 (8)
(8)
其中: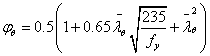 (9)
(9)
其中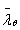 由下式求得:
由下式求得:
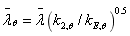 (10)
(10) 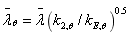 (11)
(11)
在正常的温度设计中,横截面应该分类,而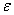 值则由(12)式给出。
值则由(12)式给出。
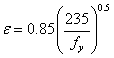 (12)
(12)
尽管这时作者来说有些不一致,Annex E of EN1993-1-2[2005]指出,4级截面室温下有效的截面性能应该确定,弯曲应力应该在室温截面性能的基础上随之确定。
(9)式中的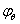 值取决于材料屈服强度,因此Eurocode3弯曲曲线不能直接与柱体弯曲测试比较。
值取决于材料屈服强度,因此Eurocode3弯曲曲线不能直接与柱体弯曲测试比较。
图8给出了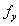 =300
=300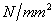 和500
和500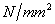 时Eurocode3曲线与可得的试验结果的比较。
时Eurocode3曲线与可得的试验结果的比较。
表8给出了临界温度下测试弯曲临界载荷与预测的弯曲应力的比较。表格9给出了残柱试验结果和预测的临界载荷的比较。
4.1.2结构不锈钢的Euro Inox/SCI设计手册
Euro Inox/SCI设计手册将室温横截面分类法运用于高温设计,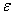 由(13)式确定。
由(13)式确定。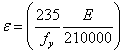 (13), 尽管Euro Inox/SCI设计手册中对
(13), 尽管Euro Inox/SCI设计手册中对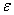 的定义不同,横截面的分类方法却没有改变,因此预定抗弯力相同。
的定义不同,横截面的分类方法却没有改变,因此预定抗弯力相同。
因此,柱体抗弯测试的结果与Euro Inox/SCI设计手册的图形比较与图8给出的EN 1993-1-2的相似。表8和9分别了测试结果与预测的柱体抗弯力及短柱抗力的数值比较,得到了与EN 1993-1-2相同的结果。
4.1.3 CTICM/CSM提案
CTICM/CSM提议了许多对EN 1993-1-2方法的改进措施,通过避免确定2%应变下的高温强度来简化计算,并提高了与试验结果的吻合度。首先,它提议高温下横截面分类法应该遵循Euro Inox/SCI设计手册中的方法。其次,它提议所有等级截面的强度减小因子应该以高温0.2%屈服强度为基础,最后它建议高温下采用prEN 1993-1-4(2004)[30]中的室温弯曲曲线,这利用(8)式,而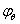 由
由
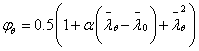 (14)式确定
(14)式确定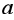 是缺陷因子,
是缺陷因子,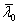 是极限细度,对于空心截面,
是极限细度,对于空心截面,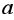 和
和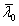 分别取0.49和0.2。
分别取0.49和0.2。
图9比较了CTICM/CSM弯曲曲线与测试结果比图显示了对于粗构件。测试结果通常被低估了,而对于细构件,测试结果通常被高估了,对粗构件测试结果的低估并不明显,由于设计抗弯力被0.2%屈服强度的使用所限,而测试数据显示可获得更大的应变。表9是短柱测试的结果,CTICM/CSM除以测试斥力的平均值是0.75,相应的变化系数为0.14。
第5部分详细讨论了测试结果与三种设计方法的比较。
4.2 梁
对1.2截面梁EN 1993-1-2(2005)中,对1.2级截面梁横截面的弯曲力矩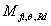 ,在给定均匀温度
,在给定均匀温度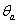 对可由式确定而3,4级截面梁的分别由(16)式和(17)式确定。对1,2截面,塑性性能由2%应变极限表征,对3级截面,弹性性能由2%应变极限表征,而4级截面性能利用了0.2%塑性应变极限。梁截面弯曲力矩
对可由式确定而3,4级截面梁的分别由(16)式和(17)式确定。对1,2截面,塑性性能由2%应变极限表征,对3级截面,弹性性能由2%应变极限表征,而4级截面性能利用了0.2%塑性应变极限。梁截面弯曲力矩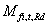 在非均匀温度下的大小由(18)式确定。
在非均匀温度下的大小由(18)式确定。
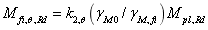 (15)
(15)
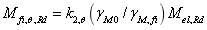 (16)
(16)
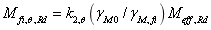 (17)
(17)
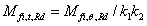 (18)
(18)
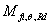 是设计时断面为均温
是设计时断面为均温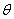 ,等同于
,等同于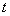 时刻的最高温度
时刻的最高温度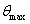 ,
,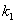 和
和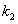 分别是非均匀温度下沿截面和沿梁长度上的修正系数。对于一未受保护的梁,三边裸露于火中,第四边支撑一块混凝土板,
分别是非均匀温度下沿截面和沿梁长度上的修正系数。对于一未受保护的梁,三边裸露于火中,第四边支撑一块混凝土板,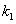 =0.7,
=0.7,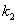 的所有情况下均取1.0。局部安全因数,
的所有情况下均取1.0。局部安全因数,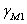 ,
,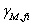 可被视作是一致的。此处不考虑不锈钢梁在火中的横向弯扭,由于试验的均为固定梁。
可被视作是一致的。此处不考虑不锈钢梁在火中的横向弯扭,由于试验的均为固定梁。
对于柱体,EN 1993-1-2提出截面应该在室温方法的基础上分类,但采用(12)给出的修正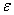 因数。Euro Inox/SCI设计手册在高温设计时采用室温截面分类方法,其它的遵循Eurocode方法。设计手册中的
因数。Euro Inox/SCI设计手册在高温设计时采用室温截面分类方法,其它的遵循Eurocode方法。设计手册中的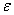 由(13)式确定,CTICM/CSM滑提出对梁的修改。
由(13)式确定,CTICM/CSM滑提出对梁的修改。
表10给出了每个梁测试中,设计弯曲力矩和测试中施加的弯矩的比较,不锈钢的设计弯曲力矩是根据EN 1993-1-2和Euro Inox/SCI设计手册确定的,在比较中,采用测定的几何和材料性能,所有的局部因数视作是一致的。比较显示,根据EN 1993-1-2方法和Euro Inox/SCI设计手册,预测的弯曲力矩除以测试值所得平均值均为0.74,变化系数为0.23。
5.设计准则修正
不锈钢柱、梁的所有测试结果都已和现行的设计准则作比较。表8-10给出的比较大体上揭示出现行设计方法的保守性和预测的不精确性,部分是由于弯曲处理的不一致性以及不适当的应变极限和构件弯曲曲线,此处做了修正。
除了材料强度和硬度在高温下衰减的相对独立性。强度和硬度的关系同样重要,由于界定了弯曲的敏感性。目前,这个已包括在EN 1993-1-2和Euro Inox/SCI设计手册中,采用了高温non-dimensional构件细度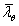 。
。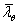 是由修正室温non-dimensiona细度
是由修正室温non-dimensiona细度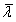 而得的。如(10)和(11)式。
而得的。如(10)和(11)式。
图10表明了不锈钢和碳钢的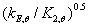 和
和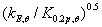 随温度的变化量,
随温度的变化量,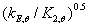 和
和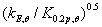 低于临界状态时导致了构件长细比的上升,象征了高温下比室温下有更大的弯曲倾向。若
低于临界状态时导致了构件长细比的上升,象征了高温下比室温下有更大的弯曲倾向。若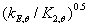 和
和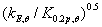 值高于临界状态,则相反。
值高于临界状态,则相反。
在室温下对局部弯曲的处理中,采用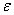 因数来补偿材料屈服强度
因数来补偿材料屈服强度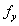 的变化。ENV 1993-1-2(2001)[31]修正了截面分类中使用的
的变化。ENV 1993-1-2(2001)[31]修正了截面分类中使用的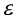 因数,反映出高温下强度和刚度并不是按同一速率衰减的。因此,高温下
因数,反映出高温下强度和刚度并不是按同一速率衰减的。因此,高温下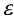 由
由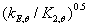 因数修正,由(19)式确定。
因数修正,由(19)式确定。
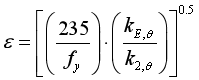 (19)
(19)
由图10可看出在大部分高温范围内,碳钢的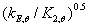 值比unity低,因此,比室温下更易弯曲,如果忽视这个特征则会导致不安全预测。为了简化计算,在EN 1993-1-2(2005)[8]中,对不锈钢和碳钢这个因数保持在一固定值0.85,从图10可清楚地得出,这个因数对于不锈钢是不合适的。
值比unity低,因此,比室温下更易弯曲,如果忽视这个特征则会导致不安全预测。为了简化计算,在EN 1993-1-2(2005)[8]中,对不锈钢和碳钢这个因数保持在一固定值0.85,从图10可清楚地得出,这个因数对于不锈钢是不合适的。
Euro Inox/SCI设计手册通过高温下运用室温分类法有效地采用了一个修正因素。这比Eurocode3处理方法更合适,但是仍然没有正确地反映出不锈钢在高温下强度和硬度的变化量。
有人提议高温下强度和刚度的真实变化量可用于截面分类,并可决定不锈钢的有效耐火性能。因此,由(20)式和(21)式确定的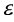 因数应在临界温度下确定,因此被用来重新将截面分类。(20)式适用于室温下的1,2级截面,并采用2%应变极限,而(21)式适用于室温下的3,4级截面,采用0.2%塑性应变极限。(21)式也用来确定有效截面性能,标记
因数应在临界温度下确定,因此被用来重新将截面分类。(20)式适用于室温下的1,2级截面,并采用2%应变极限,而(21)式适用于室温下的3,4级截面,采用0.2%塑性应变极限。(21)式也用来确定有效截面性能,标记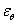 用来与室温设计时的
用来与室温设计时的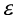 因数相区别。
因数相区别。
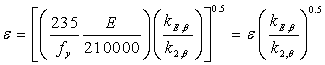 (20)
(20)
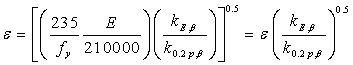 (21)
(21)
从图10中可看出不锈钢的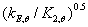 和
和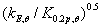 在高温下比unity高,在临界温度下,截面重新分类和重新确定有效截面性能的结果是有益的,室温下的4级截面可能在高温下完全有效。
在高温下比unity高,在临界温度下,截面重新分类和重新确定有效截面性能的结果是有益的,室温下的4级截面可能在高温下完全有效。
进一步提议说在确定截面和构件耐火力时,1,2级截面的强度减小因子应基于2%应变极限,3,4级截面的应2%塑性应变极限如现行设计准则所述。对3级截面采用2%应变下的强度是不合理的,由于可能在达到应变水平前发生局部弯曲。本文第4节中与现行设计方案中作比较的试验结果被重新评价。结果见表8-10,对于柱体,修正的弯曲曲线与试验结果较吻合,这是通过采用(8)式和(14)式的室温弯曲曲线而得,并选择了合适的缺陷参数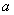 值和极限细度
值和极限细度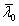 ,对结果的分析显示其中有一柱体在室温下为4级截面,在高温下变成了2级截面,它的耐火力被高估了。在进一步的测试结果中,室温下的4级截面不可能在高温下变为3级以上截面。
,对结果的分析显示其中有一柱体在室温下为4级截面,在高温下变成了2级截面,它的耐火力被高估了。在进一步的测试结果中,室温下的4级截面不可能在高温下变为3级以上截面。
对于柱体弯曲,计算值除以实测抗力的平均值为1.00,变化系数为0.15。
对短柱,计算值除以实测抗力的平均值是0.91,变化系数是0.15。
而对梁,计算值除以测试抗力的平均值为0.84,变化系数是0.19。
提出的不锈钢柱、梁的更为合理的耐火设计方法与Euroal方法相比,钢柱弯曲抗力提高了6%,残柱抗力提高了28%,平面弯曲抗力提高了14%。
6.结论
高温下,不锈钢有着比碳钢优越的强度和硬度保持力,这是由于合金元素的有益。这在EN 1993-1-2(2005)中得以反映,然而,除了高温下强度和硬度衰减的相对独立性,强度和硬度的关系同样重要,由于这决定了弯曲敏感性。
校对和分析了23个柱体,6个残柱,6个横向固定梁的耐火测试结果。测试被有选择性地数值再现了,研究了局部和整体初始几何缺陷,残余应力,角部强度增强性和构件末端的局部保护,从测试与数值研究的比较来看,可知有限元模拟能够再现不锈钢构件在火中的非线性大挠度反应。
提出了修正的不锈钢弯曲曲线,一致的应变极限和一个新的截面分类方法以及对局部弯曲的处理。这些修正导致了对不锈钢柱、梁在火中弯曲的更有效,更一致的处理柱体弯曲抗力提高了6%,短柱提高了28%,平面弯曲抗力比现行的Eurocode方法提高了14%。



