鲁棒迭代学习控制及其在注塑成型工艺中的应用

摘要

融合是迭代学习控制（ILC）在批处理过程中的设计和应用中的一个重要问题。 本文提出了一种稳健的迭代学习控制器的设计。以确保BIBO（有界输入 - 有界输出）稳定被导出为最优ILC，当跟踪任意有界输出参考时。一个实际的方案,加权矩阵的选择过程也提出了不确定的初始复位和干扰,确保系统批次的性能改进。最后,应用注塑控制演示e5ectiveness算法。2001 Elsevier Science Ltd.保留所有权利。

关键词：迭代学习控制; 批量处理; 注塑成型

1.简介

迭代学习控制（ILC）的动机是模仿人类学习过程。它最初的开发是为了操纵需要以高精度重复给定的任务的工业机器人。通过使用过程的重复性，即试验（或批）指标k从试验到试验，以及经过的时间指数在一步一步的审判中，ILC逐渐和两次迭代地提高了控制精度控制输入的尺寸。这二维学习结果优于常规饲料 - 背部控制技术，只有时间尺寸沿着时间轴进行输入动作。 学习控制设计的关键是提供一种算法，以确保为下一次试验生成控制输入，使得性能随着每次连续试验而提高。Uchiyama（1978）引入了迭代学习的产生方法，后来由Arimoto，Kawamura和Miyazaki（1984）进行了数学计算。此后，对迭代学习控制的发展和分析已经有了大量的研究。 最近，ILC被应用于许多重复工艺，如间歇式反应器，分批蒸馏和注射成型（Lee，Bang，Yi，Son，＆Yoon，1996; Havlicsek＆Alleyne，1999）。Bien和Xu（1998）的参考文献可以找到关于这个问题的综合文献调查。

传统的ILC方案用作开环前馈补偿器。然而，已经发现，不用于循环反馈的ILC通常对扰动敏感，系统收敛趋于缓慢（Bien＆Xu，1998）。最近，Amann，Owens和Rogers（1996）通过将Riccati反馈与基于优化原理的典型ILC前馈相结合，提出了一种新的ILC算法。该方案具有步进自动确定的优点，因此保证了指数收敛。模拟显示，Amann的最优学习算法非常有效，与传统的ILC方案进行比较; 这提高了对工业设置的更广泛应用的期望。在现实中，流程干扰中总是存在不确定性，而且，初始化过程很可能不是完全可重复的。这些实际问题对许多批次工艺是重要的，例如注射成型。 这些问题在阿曼的原始文章中没有得到解决。

本文旨在扩展Amann，Owens和Rogers（1996）的最优迭代学习控制算法，以应用于具有不确定初始复位的不稳定干扰的通用批处理。Su。确保ILC具有有界输入有界输出（BIBO）稳定性的必要条件。对成本函数的加权矩阵的选择进行分析。最后，给出了使用引入的最优迭代学习控制来控制注塑速度的模拟和实验应用，以证明所提出的算法的效果。

2.最佳学习控制背景

Amann最优学习算法的背景介绍如下。

2.1  问题制定

假设感兴趣的植物由具有干扰的以下采样时间线性系统描述

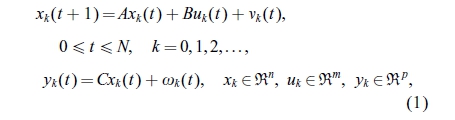
其中下标k表示对应于试验索引的操作的迭代次数，例如，yt（t）是在时间t的系统输出的值;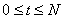 ; 在第k个操作。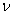k（t）和k（t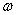）表示有界状态和外部干扰。 注意，方程式的精确状态初始化。（1）对于每次迭代都不是必需的。本文将讨论初态变化和外部干扰的鲁棒性。状态空间矩阵A，B，为了简单起见，假设C是不随时间而变的。没有任何技术学科，有可能将本文的所有结果扩展到时变系统。基于线性系统理论 （1）可以推断：

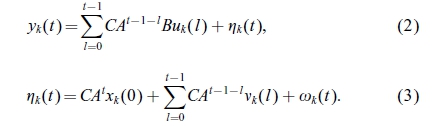
从上述可以看出，每次试验的初始动作和干扰出现在植物中，将Amann，Owens和Rogers（1996）的工作扩大到更普遍的情况。在每次试验中，涉及9个时间间隔。 （2）可以以矢量形式通过建立超向量YK作出; uk和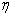k从yk（t）; uk（t）和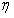k（t）如下：

其中

超向量都带有参数时间t的遗漏。在实施迭代学习控制期间，以前的试验的yk和uk需要记住当前试验的uk + 1（t）的计算。矩阵G，已知为托普利兹矩阵一个三角形下部块矩阵，可以从第9列来确定。在本文中，由阿曼，欧文斯和罗杰斯（1996）认定为“规律性条件”

假设ker GT = 0。如果植物，方程 （1）具有相对度1，即CB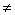0，那么G在SISO情况下是可逆的。否则，如果CB = 0，则可以按照Amann，Owen和Rogers（1996）和Silverman（1969）的作品中的详细描述进行正规化程序。这种规律性条件确保GTG（或GGT）具有至少一个正特征值。基于这个假设，与Amann，Owen和Rogers（1996）的收敛证明将在第3节中给出。

定义2.1 （Amann，Owen，＆Rogers，1996）。迭代学习控制算法是因果关系，在第（k + 1）次试验/实验时刻t对系统的控制输入的值仅从在时间间隔[0;（k + 1）次试验中可获得的数据计算） t]和以前的试验。

2.2。 优化迭代学习控制器

考虑以下由系数矩阵A组成的标称系统; B和C等式 （1）：

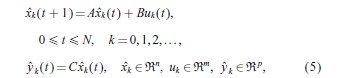
其中带有上标“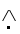”的变量表示标称系统输出，它们由零初始化。它们在没有任何干扰和初始误差的情况下代表方程（1）的系统输出。对于第（k + 1）个试验中给出的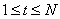的参考轨迹（或期望的系统输出）r（t），通过最小化相对于uk +1（t）的以下二次性能指标来获得标称最佳迭代学习控制律：

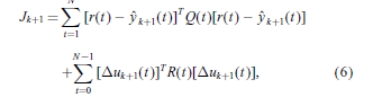
其中Puk + 1（t）= uk + 1（t）-uk（t），加权矩阵Q（t）和R（t）对于所有t是任意对称正定。索引函数 （6）可以以矩阵形式被重写

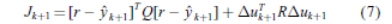
其中 Q=diag{Q(1), Q(2), …,Q(N)}; R=diag{R(0);

R(1), … , R(N − 1)},

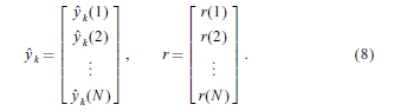
通过将公式（7）的偏导数相对于uk + 1，得到标称最优控制输入

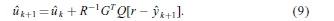
然而，可以观察到，对 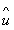k + 1（t）的计算，等式（9）的算法不是偶然的，因为通过该控制定律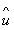，k + 1（t）将取决于 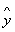k + 1（t’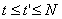）。在Amann，Owens和Rogers（1996）之后，下面可以给出等价形式的（9）

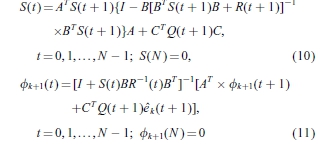
其中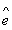k（t + 1）= r（t + 1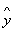）-k（t + 1）。 因此，得出新的公式

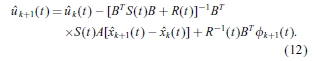
这表明，如果标称状态XK和调整输出y K含量由标称系统引入的因果标称控制输入可以被迭代地获得，式（5）。这种迭代学习控制算法在应用于等式（4）的情况下也是最佳的，其中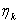 = 0，即无干扰情况。本文旨在开发一种存在不确定的初始和干扰的ILC算法。这可以通过用公式（10） - （12）中的标称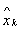和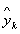与系统的xk和yk的等式（1）的测量，计算uk来实现。因此，因果迭代学习控制算法可以归纳为

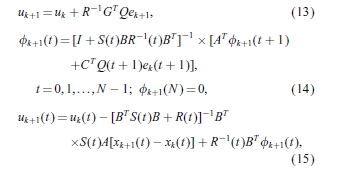
其中S（t）由式（10）获得。可以看出，由方程（10）和（13） - （15）组成的控制算法是因果关系。在公式（15），uk+ 1（t）由通过将当前试验的反馈作用改善最后试验输入UK（T）而获得（等式（15）的右侧的第二项））和前馈动作（等式（15）的第3项），其代表先前试验的信息。

在 Amann, Owen，和Rogers（1996）的工作中，还缺乏关于加权矩阵Q和R为系统收敛的选择的准则。这种实际考虑在ILC到批量处理的设计和应用中是重要的。上述方法的收敛和鲁棒性分析在初始化和扰动的不确定性的基础上进行，并以喷射速度控制为基础。

3稳定和收敛分析

对于所提出的算法，将研究如下所示的鲁棒有界输入边界输出稳定性。

定义3.1。据称，迭代学习控制系统是鲁棒的BIBO（有界输入有界输出），迭代学习控制系统被称为鲁棒BIBO（有界输入有界输出）

上述设计考虑了系统的扰动和沿试验轴的初始化不确定性。讨论了稳健的BIBO稳定性以及迭代学习控制算法的收敛性和鲁棒性。

定理3.1（稳健BIBO稳定性）。方程（10）和（13） - （15）到植物（1）的迭代学习控制算法的应用是稳健的BIBO稳定，如果， 只有当 I + GR-1GTQ和I + R-1GTQG具有其单元外盘全部特征值， 那么

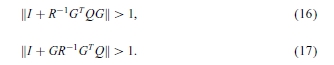
证明。 将等式（13）乘以G并根据方程（4）和ek = r-yk得到

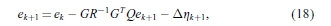
其中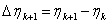。 然后沿着试验指数k的ek的迭代关系如下

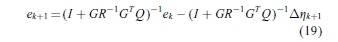
再次将ek + 1 = r-yk + 1替换为式（13）并使用式（4），则可以得出

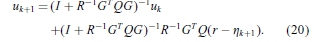
结果如下：应用标准离散时间系统理论。

定理3.2（收敛）。将等式（10）和（13） - （15）的迭代学习控制算法应用于方程（1），其中选择R和Q以满足方程（16）和（17）。如果所有试验都是重复的，因为所有的xk（0），外部干扰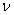k（t）和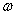k（t）与试验指数k相同; 那么以下收敛结果将成立：

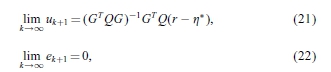
其中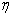*是一些常数向量。

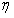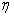证明。如果所有试验都重复，则从公式（3）可以看出，对于所有试验指数k，存在一个常数向量*，使得k =*。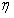

迭代地使用方程（20）和（19），得到

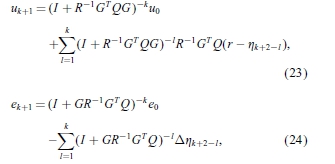
分别。 因此，在定理3.1的稳健BIBO稳定条件下，得到

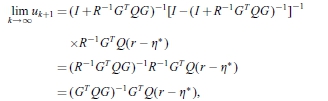
这完成公式（21）。

由于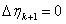，由公式（24），容易得出式（22）的极限。

4.加权矩阵的选择

上述稳定性推导是基于初始误差和扰动有界的假设。为了实现合理的瞬态性能，必须仔细选择加权矩阵Q和R。令R =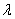I，Q = 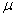I其中？ 并且是正设计常数，并且让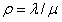。注意，最优ILC的性能受到Q和R的比值而不是其实值的影响，如方程（16）和（17）所示。

一个必要的条件，必须满足由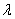和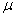是保证鲁棒有界输入有界输出稳定性。如果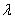和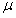均为正，则公式（16）和（17）是直接的，而GTG或GGT具有至少一个正特征值。以下是确定常数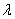和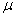，使得所得到的控制系统不仅可以拒绝不确定的干扰，而且可以快速收敛来跟踪期望的参考。它来源于方程（13） - （15）

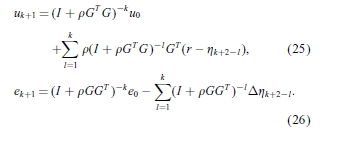
因此，对于固定GGT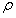，值（相当于大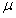）的大值有助于减少第一次试验e0的误差，即可以通过试验实现快速收敛。然而，从式（14）和（15）可以得到

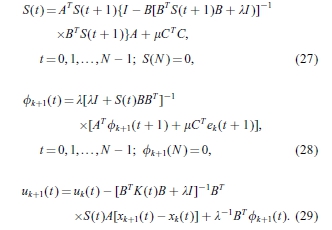
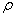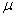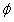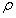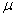可以看出，大的（或大）导致在uk + 1（t）到k + 1（t）之间的更强的前馈动作，使得控制系统对输出参考的变化较不敏感。强劲的前馈行动往往会因不确定性和外部干扰而导致随机误差的积累，从而导致控制投入的强劲增长。另一方面，从等式（3），（19）和（20）可以看出，当A在单位盘外部具有特征值时，初始化不确定性和外部干扰可能导致慢收敛或甚至振荡控制。因此，建议采用不同的加权方案来考虑这些实际考虑因素。 令k = k/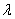k是当k→∞时随着周期数k的增加而接近零的序列，即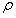k →0（或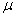k→0）。 那么方程式 （10）和（28）成为

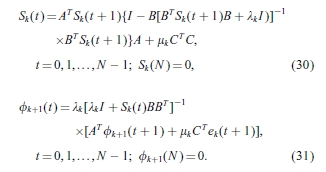
当k→∞时，Sk（t）→0和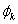（t）→0很明显，这表明通过定理3.1和式（15）可以确保uk（t）和ek（t）的快速收敛。在以下部分中，通过实验验证了选择加权矩阵Q和R的建议方案。

5.注射速度控制的仿真与实验应用

5.1  注塑工艺

注塑成型是重要的聚合物加工技术。它将聚合物颗粒转变成各种形状和类型的产品，从简单的杯子到精密镜头和光盘。作为循环过程，注射成型包括三个阶段：填充（注射），包装保持和冷却。在填充过程中，注射螺杆向前移动并将聚合物熔体推入模腔。一旦模具完全被覆盖，该过程就切换到填料保持阶段，在此期间，在一定压力下将额外的聚合物加入到模具中以补偿与材料冷却和固化相关的收缩。 包装保持阶段继续，直到模具腔的狭窄入口的门冻结，将模具中的材料与注射单元中的材料隔离。 在冷却阶段，模具内部的聚合物继续冷却，同时通过螺旋旋转将材料熔化并输送到桶的前部。 然后重复该过程。 如图。 图1显示了具有仪器的典型往复式螺杆注射成型机的简化图。

许多研究人员已经表明，对每个阶段的一些关键变量的精确控制对于模制件的质量是至关重要的。 注射速度是注射阶段的关键变量。 注射速度的动力学被发现是非线性和时变的，它受到材料性能，注射模具和操作条件的变化等许多因素的影响（Tsoi＆Gao，1999; Yang＆Gao，2000 ）。

Havlicsek和Alleyne通过建立一个仅限于机械液压系统的数学模型，忽略了材料，模具和其他操作条件的不合格，应用了ILC来控制电液注塑机的柱塞位置和腔压力。 。 注射速度既不测量也不直接控制在其工作中。 喷射速度动力学的数学模型是相当复杂的，因为它不仅受到机械液压系统的影响，还包括所使用的材料和模具几何特性。 重要的是要注意，材料和模具的选择取决于待模制的产品，注塑成型中使用的聚合物表现出强烈的非线性Qow和热行为。在本文中，基于方程（13） - （15）的学习控制器被设计和实现以直接控制喷射速度。 首先进行了仿真，研究了理想情况，没有干扰和初始化误差的线速度模型。 然后对非线性过程进行在线实验控制，改进以提高所提出的控制器的瞬态性能。

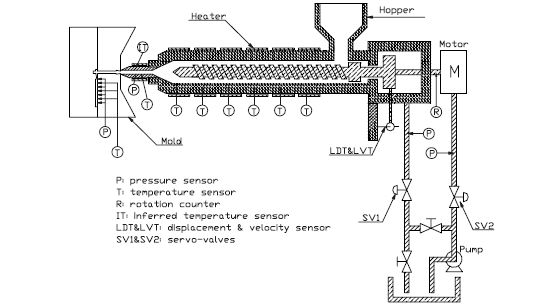
图1.注塑机和仪器图。

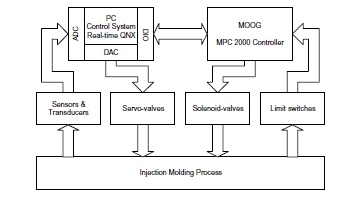
图2.整个成型过程控制系统的简化图。

5.2 实验装置

本机使用的机器是陈顺松螺旋注塑机型号JM88MKIII。 该机的最大夹紧吨位为88吨，最大重量为128克。

整个控制系统的简化框图如图2所示，注射成型机的仪器可以在图1中看到。速度控制系统由速度传感器，伺服阀，MOOG MPC 2000控制器 ，以及具有扩展I / O系统的个人计算机（PC）。如图1所示，已经安装了类型为RH-N-0200M的Temposonics系列III型位移=速度传感器，用于测量喷射位移和速度。快速响应线性MOOG伺服阀（SV1）（Thayer＆Davis，1980 ），J661-141型，配有液压系统以控制喷射速度，如图1所示。 MPC 2000控制器适用于控制机器序列和机筒温度。在Pentium 133 MHz PC机上安装了两个数据采集卡：国家仪器AT MIO 16X卡提供数模转换（DAC）和模数转换（ADC），以及AT DIO 32F数字I / O卡进行数字输入输出的PC和MPC 2000一套实时的节目已经在内部使用C语言开发的，在QNX实时多任务操作系统下之间（DIO）通信（版本 4.2），执行注塑过程的数据采集，控制和运行同步。

按照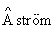和Wittenmark（1995）的指导原则，速度控制器的采样速率确定为5 ms。

用于所有实验的具有图3所示几何形状的MOOG杯模具。 本工作中使用的材料是高密度聚乙烯（HDPE）（SABIC，Ladene）和聚丙烯（PP）（Pro-fax，HMC Polymers）。

5.3  模拟

在实验前进行仿真，以理想条件测试控制算法，无干扰和初始化误差。使用开环测试结果确定了模拟模型：引入过程输入（图1中SV1的伺服阀打开）的阶跃变化来激发该过程，并记录相应的注入速度响应，然后 分析 在将MATLAB系统识别工具箱转换为状态空间模型之前，使用MATLAB系统识别工具箱识别自回归（ARX）模型，如下所示：

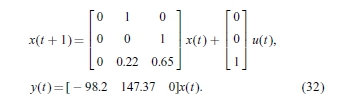
在以下的模拟和实验中，仅使用状态变量x1（注射速度）的测量。

最优学习控制算法应用于系统（32），简单加权因子Q = R = 1。 控制系统按照图4（a）中实线所示的步进变化设定点。 第9周期的控制输入随机设置为0.04。 所得到的输出响应如图1所示。 图4（a），相应的控制输入如图4（b）所示。如预期的那样，第一个周期的系统输出远远不到设定点。 系统输出响应在第二个周期内迅速收敛。 第6循环和第10循环的系统输出显示了完美的设定点。 该模拟清楚地表明，最佳ILC可以非常好地控制过程，而无干扰和初始化错误。 在模拟中注意到，控制器在设定点阶跃变化之前提前几步改变控制输入，导致完美的跟踪无延迟。 这是ILC的固有优势。

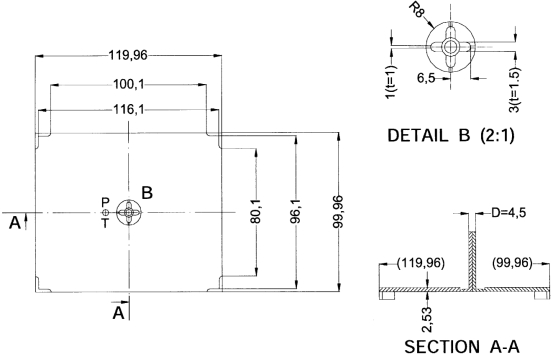
图3. MOOG模具的几何图。

通过这样优秀的模拟结果，最优ILC被实验应用于实际注射成型过程，这是一个具有干扰和初始化误差的非线性过程，具有上述选择的简单加权矩阵Q和R.

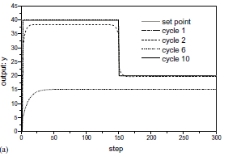
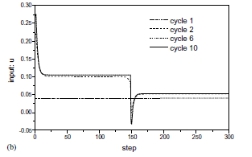
图4.使用最优学习控制的模拟结果，Q = R = 1。

（a）输出y，（b）相应的输入u。

5.4 实验结果与讨论

最佳迭代学习控制应用于实验使用材料HDPE的注射速度控制。作为模拟情况，加权矩阵Q和R都被选择为1。 喷射速度被控制以跟随阶跃变化。如图5（b）中的短划线所示，初始输入信号，即第9周期的控制输入被任意设定为10％。控制结果绘制在图5中，其中图5（a）示出了喷射速度响应（输出），图5（b）示出了相应的伺服阀开口（输入）。 可以看出，随着循环数k的增加，控制响应变得振荡，与早期获得的模拟结果相矛盾。实验控制性能差的原因与初始化不确定性和干扰的积累与选择的强前馈动作有关。在最优ILC设计中，线性时间不变模型用于近似注入速度的动力学，这是非线性和时变过程，不可避免地存在显着的模型不匹配。由于电液系统的性质，初始喷射速度响应不能精确重复，导致喷射速度控制的初始化误差的不确定性。此外，在来自不同来源的成型过程中存在干扰，例如材料的变化和/或操作条件。随着干扰和模型不匹配的存在，大的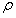导致强大的前馈动作和弱反馈动作。结果，减少了所提出的学习控制器的错误拒绝能力。

实施第4节提出的方法。 因此，控制器用变化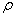进行修改，以确保系统收敛并提高最优ILC的鲁棒性。对于第一个周期，控制输入设置为与最后一个实验相同的10％的常数值。 然后用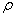= 1：0计算公式（27） - （29）中的增益矩阵S（t）和前馈项，以确保快速的控制响应收敛。对于以下周期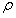，被设置为随着周期数k的增加而指数地减小，在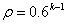的关系中。使用材料HDPE作为最后一个实验，并且速度被控制以遵循与先前情况相同的阶跃变化曲线。所得到的速度响应在图6（a）中给出，其中相应的阀开口如图6（b）所示。 可以观察到，如图6（a）的虚线所示，第二循环的速度响应迅速收敛。 第六个循环的控制已经通过虚线划分而已。 实线显示了第十个周期的结果，尽管液压系统的Qow和电荷引起的初始注入阶段的延迟，速度跟踪设定点轨迹。 显然，在实施拟议修改后，控制振荡已被消除。 控制响应快速收敛，控制系统随着循环次数的增加而稳定。

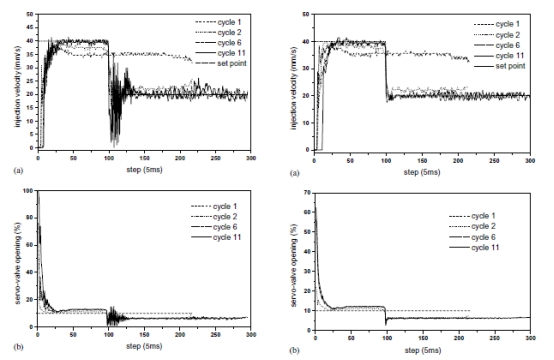
图5.使用恒定加权矩阵（HDPE）         图6.使用改变加权矩阵（HDPE）的

的最佳学习控制的实验结果。               最优学习控制的实验结果。

（a）喷射速度，（b）相应的阀门开度。   （a）喷射速度，（b）相应的阀门开度。

非线性和时变特性表明注射速度动力学随着工作点而变化，并且它们高度依赖于在模制过程中使用的材料。使用如图7（a）中的黑色实线所示的具有弧形设定点轮廓的不同材料：PP进一步测试修改的最佳ILC。 第一个循环的控制输入随机设置为7％。 结果如图7所示。速度响应迅速收敛; 第6和第11周期的响应彼此重叠，表明在不同的成型条件下修改的最佳ILC的良好性能。

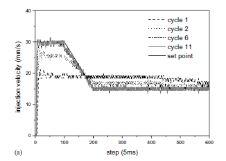
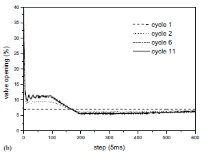
图7.使用改变加权矩阵（PP）的最优学习控制的实验结果。

（a）喷射速度，（b）相应的阀门开度。

6。结论

本文针对不确定的初始化和扰动过程，已经考虑了基于最小化二次性能标准的最优迭代学习控制算法的鲁棒性和收敛性问题。已经建立了一个非常有必要的条件，以确保迭代的鲁棒BIBO稳定性 跟踪任意有界期望输出时学习控制系统。 通过修改二次成本函数的加权矩阵，通过注塑成型过程的应用，已经提高了性能。 该算法的成功应用使得有希望的是，通过适当地调整二次索引的加权矩阵，可以将最优迭代学习控制应用于其他工业批量工厂，特别是具有不确定的初始化和干扰的过程。

香港科技大学化学工程系，香港B研究信息与控制中心，大连理工大学。