美国飞机工业协会科技2014-1529

美国飞机工业协会科技

1月13至17年，马里兰州国家港口

第五十五届美国飞机工业协会/美国机械工程师协会/美国土木工程师协会/美国直升飞机协会/ 高级科学计算机的结构，结构动力学，材料会议

概率损伤容限分析的序列重要性抽样

基思戟*和勒鲁瓦M.菲茨沃特†

波音飞机公司，芝加哥，伊利诺斯，60605

概率损伤容限分析由一个不确定的方法来评估一个维修策略的损伤容限的结构部件受退化，如疲劳裂纹。在这种方法中，进行了一个维护策略的分析，以确定是否保持指定的安全级别，作为测量由单一飞行的概率的故障，并预测未来的维修。描述了一种通过飞行服务生命飞行所得的采样方法，并对模型进行了修正，可以很容易地估计出故障的单次飞行概率。通过实例表明，该方法可以匹配的直接采样蒙特卡洛模拟的结果，这些结果相比，一个流行的软件包。此外，这种方法的灵活性，证明通过求解一个扩展版本的问题，是更现实的和不能解决使用目前可用的软件。

命名

CDF

DS

=  累积分布函数

=   直接采样

FH

=   飞行小时

IS

=  重要性抽样

MC

=  蒙特卡洛

PDTA

POD

PF

=   概率损伤容限分析

=   检测概率

=   粒子滤波

PROF

SFPOF

=   骨折概率（戴顿大学研究院软件）

=   单一飞行故障概率

Ⅰ  简介

概率破坏公差分析(PDTA)涉及维护策略的评估航空航天结构受疲劳裂纹而将各种量表示为随机变量,而不是传统的确定性方法破坏公差分析。在第二部分评审PDTA问题。在以前work1本文的作者提出了一个直接抽样(DS)蒙特卡罗(MC)方法单一飞行失效概率的估计(SFPOF)组件受疲劳裂纹可能会或可能不会包括未来安排检验。结果表明,一个受欢迎的PDTA工具称为Fracture2概率,或PROF,倾向于高估SFPOF例如文档的问题。虽然DS MC程序是有效的,但它是低效的,因为它利用直接输入随机变量的抽样估计的概率出现罕见的事件。MC常规的结果,而耗费时间,可用于验证其他方法由于DS MC背后的逻辑是很容易防守。DS MC常规第三章总结了。

序贯重要性采样3 PDTA问题提出方法。传统的重要性抽样(是)需要增加抽样的样本空间的一部分将有助于更快的收敛的MC估计。序贯重要性采样的扩展是一个持续的进程或时间序列。这种方法是一种粒子滤波(PF)——注意PF缩写是引用中使用这种方法,详细讨论了在第四节。V节几个PDTA问题描述和使用讨论解决方法。PDTA PF方法是非常灵活的,可以解决更复杂的版本的PDTA问题;这是在第六部分通过描述和解决一个扩展示例问题,允许更多的现实主义关于后裂纹修复的行为。最后,发现第七节和结论进行了总结。

II  PDTA问题说明

本文的分析仅限于特定的表征PDTA问题;专门PROF所描述的软件的问题(尽管一个扩展是在第六节)。这个问题范围定义如下:

l 0秒时存在缺陷,这是一个随机变量的大小

l 断裂韧性是一个随机变量

l 裂纹扩展是一个确定性的函数运行的飞行小时

l 归一化应力强度是一个确定性的裂纹长度的函数

l 最大作用应力/飞行是独立于flight-to-flight和遵循概率分布

l 裂纹大小、断裂韧性和最大作用应力/飞行是相互独立

这种分析的目标是为每个航班估计SFPOF寿命和裂纹检测的概率估计(PCD)为每个安排检查。SFPOF使用以下定义:

对于单个组件,单航班(SFPOF)的故障概率,对指定的未来飞行,结构失效的概率会发生在指定的飞行,考虑到结构幸存了下来,飞行和允许恢复或执行预防性维护之前飞行。SFPOF提出如下方程澄清解释。每个飞行是一个离散事件的组件要么生存要么它会失败。假设是飞行的失败,代表补充飞行(生存),飞行的兴趣。事件之前,所有航班生存和感兴趣的飞行失败

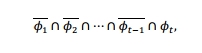
这是书面的概率

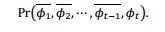
这不是SFPOF,相反,SFPOF感兴趣的飞行失败的概率是给定前一航班的生存。指出生存或失败的后续航班不是独立的,得到如下:

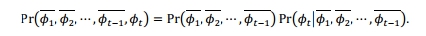
在上面的方程SFPOF是第二个因素。以下方程利用DS MC常规:

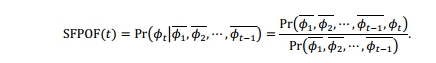
PROFv3.1使用故障率计算SFPOF方法。根据PROF手册《故障率函数…被定义为生命的条件概率密度时,考虑到结构历经时间t》。这是一个连续时间的解释,而不是一个序列的表示的航班为一系列离散的事件。PROF的做法是不被认为是这项工作从理论的角度来看,相反,只是PROF的结果比直接抽样方法。这是一个连续时间的解释,而不是一个序列的表示的航班为一系列离散的事件。PROF的做法是不被认为是这项工作从理论的角度来看,相反,只是PROF的结果比直接抽样方法。

最明确、直观的方法来计算生命周期flight-by-flight SFPOF是模拟,只有移动到下一个航班上使用寿命如果当前飞行。当故障发生时,停止试验,因此所有故障发生后生存——即之前的航班。,对于飞行t这是事件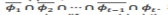SFPOF可以使用上面的公式计算的任何飞行寿命提供有足够数量的试验。这种方法是描述在下一节中,其中一些额外的细节关于概率破坏公差分析。

III  直接采样(DS)蒙特卡罗(MC)方法

估计的SFPOF对应于上述定义可以通过反复模拟结构特征的生命周期和观察第一次失败。每个生命周期由一个MC审判。在每个试验中生成必要的变量是直接从各自的概率分布和整个生命周期模拟flight-by-flight直到失败是观察。例如,如下几个试验将继续进行。

l 试验1:飞行1幸存,飞行2幸存…飞行6544幸存,飞行6544失败

l 试验2:飞行1幸存,飞行2幸存…飞行5212幸存,飞行5213失败

l 试验3:飞行1幸存,飞行2幸存…飞行7104幸存,飞行7105失败

SFPOF可以估计任何选定航班给予足够的MC常规的试验。假设有试验,是飞行感兴趣的n,是失败的第一次飞行t试验,r1是一个指标函数i和I,等于1时,声明是真的,否则0。SFPOF是首次失败飞行试验的比例除以生存飞行t的比例,或

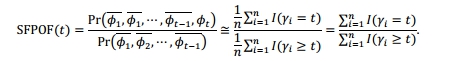
三个随机变量是参与解决PDTA问题使用这种方法:初始裂纹长度a0,断裂韧性kc,每个航班的最大作用应力, σmax、a0和kc是每个常数未知但不改变flight-to-flight在审判。一个独立于从flight-to-flight flight-to-flight和其值的变化。因此在每次试验中单个值的a0,kc的单个值,一个值的σmax飞行必须生成的使用寿命。

此外,可能会有安排检查在使用寿命(假设检验时间提前设置)。在每个试验中裂纹长度是已知的,包括检查的时候。检测概率(POD)曲线是利用——指定检验方法的能力——确定的概率发现裂纹。在给定的检验,如果裂纹尺寸a,发现裂纹和修复的概率圆荚体(a)。来确定裂纹试验中发现,生成Bernoilli随机变量(即有偏见的硬币翻转)。如果发生维修然后生成一个新的裂纹大小a0,这次从修复的初始裂纹尺寸分布、MC试验仍在继续。如果没有找到另一方面裂缝,裂缝的长度a试验仍在继续。流程图为单个试验的DS MC常规。

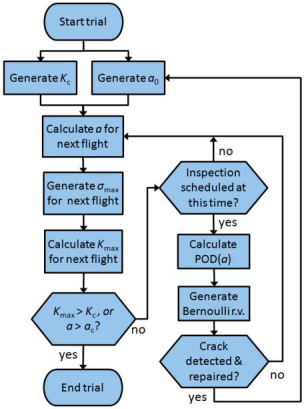
III-1 -直接抽样蒙特卡罗程序

上面描述的DS MC常规相当缓慢的收敛,因为特定的未来战斗的失败是一种罕见的事件。如果没有检查的重要性抽样修改上面的可以使用,这样收敛迅速发生。在下一节中讨论,讨论仍在部分V。

IV 序贯重要性采样方法(即粒子滤波)

在IS中,样本空间的部分最感兴趣的是取样更频繁。在MC方法获得无偏估计,计算每个样本的重要性权重值。不寻常的采样点越多,降低体重。与MC DS估计获得通过算术平均每个样本的估计。是,利用加权平均代替。之前的讨论。这不是一个完整的治疗和纯粹是为了指出相关的方面。让x1,x2 ....xn ，n独立同分布(先验知识)从一个分布密度f(x)。那么x的期望是:

在许多情况下可以更高效的如果有增加模拟抽样在某些特定地区。这是通过利用抽样分布g(x),而不是实际分布f(x),抽样分布的选择,这样的支持是相同的(f(x)和g(x)可以产生相同的值),g(x)是重的密度比f(x)在该地区的利益。假设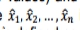i.i.d.样本的大小n从密度分布g(x)。被定义为的权重函数

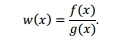
在这种情况下,(公正)X期望是:

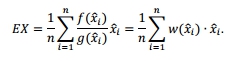
注意,一个国家可能是由多个随机变量表示。在PDTA问题状态是由断裂韧性kc和裂纹长度a。实际和采样联合分布fa,kc(x,y)和ga,kc(x,y)。这种并发症并不困难,因为a 和kc是独立的(更多内容见下文)。

IS的扩展可能是用于一个演进的过程。在序贯重要性采样方法——或PF方法获得的初始状态可能通过DS或。在这种方法中每个样本被称为一个粒子,因此每个粒子是一个向量的参数定义粒子。每个粒子的参数之一是重量。每个粒子的重量可以随时间变化的证据是观察和在这种方法中权重的总和必须通过规范化管理,他们总是和一个。

更正式,模型的状态是由x0,x1,……xt,t是当前飞行和每个x是一组向量值粒子,每个指定的模型参数值。一般参数组成状态是不明显的。这个过程必须一阶马尔可夫过程,这样下一个状态只依赖当前状态。这可以写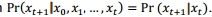除了可能存在可观测量y0,y1,....yt,与xs有关。观察y是条件独立假设x是已知的当前状态。结果;也就是说,yt只取决于xt。在任何时间t的一组n粒子加权表示当前状态的近似分布考虑到以前的观测, 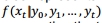。每个粒子的权重wi代表每个粒子代表真正的底层的相对可能性状态,和。

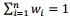PDTA这个实现的问题,单个粒子为裂纹长度由价值a,kc断裂韧度值和一个重要性重量w。也就是说,粒子Xi向量值: 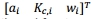。国家的进化从flight-to-flight一阶马尔可夫由于裂纹长度和断裂韧性在下次飞行只取决于这些值为当前飞行。SFPOF失败的概率是生存的利益,因此在每个航班的调整权重来反映失败之前并没有发生。为此,在每个飞行模型条件生存之前的航班,包括一个可观测量yt飞行t的代表生存。这空调是一个贝叶斯规则的应用。模型通过使用寿命flight-by-flight,利用贝叶斯规则更新粒子权重反映了证据表明前飞行t - 1幸存下来,即yt-1=TRUE. 这些粒子有一个相对较高的失效概率在前面飞行不太可能代表真相,因为没有发生故障。注意,失败并不显式地发生在PF常规;相反,每个航班的失效概率计算,随后有人断言失败不会发生(调整重要性权重结果)。表明,这种生存条件收益率SFPOF结果可比性的DS MC常规也明确模拟故障(利用降低样本大小来反映之前发生一些故障)。

有几个发行版之一必须能够样本为了利用这种方法。首先,必须能够生成初始状态x0,通常提出的一些问题因为方便分布的家庭可以选择每个随机变量来表示。接下来,过渡分布,需要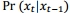,它定义了如何演变从一个飞往下一个状态。PF过渡通常是随机分布,但它可能是确定的。最后,一个必须能够计算可能性分布、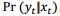,可观测变量的可能结果的概率(s)在时间给定状态的时间t。

在PROF-style PDTA分析,从flight-to-flight过渡是决定性的,因为确定性假设裂纹增长,因为kc是未知常数从flight-to-flight认为是不变的。最后,每个航班的可观测变量的生存,因此yt∣xt是一个布尔值随机变量,必须能够计算单个航班的生存概率给定的当前状态。这是在下面讨论。

粒子的集合是一个近似n的联合分布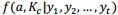对于任何飞行t。因此这组可以用来估计任何数量的兴趣是a0的函数或kc,如SFPOF或纤毛运动。方法本质上是由计算每个粒子的估计如果a0的值和kc粒子是真理,和随后采取加权平均(根据重要性权重w)获得MC的估计。金刚石是低于SFPOF的计算和详细的单粒子,后来一个例子显示了粒子滤波PDTA运行n = 3粒子组成。

记得,对于一个给定的飞行感兴趣的变量是裂纹长度、a,断裂韧性,kc,每飞行最大作用应力, σmax,归一化应力强度,k/σ (这是一个确定性的函数裂纹长度)。注意假设裂纹扩展的程度在一个航班可以忽略不计。飞行中a,kc是已知的(如计算给定粒子)的情况下,失败的概率,飞行很容易获得,如下所示。注意,在这种分析粒子失败有两种方法:

l K>Kc

Ø 应力强度超过断裂韧性

Ø 首选的失效模式

Ø 最大应力强度的值是飞行的兴趣,所以经常写成kc

l a>ac

Ø 裂纹长度超过临界裂纹长度,ac

Ø 不可取的失效模式,因为这通常表示确定性损伤公差分析提供输入是不完整的

Ø 这包括失效模式的必要性,因为输入破坏公差分析表必须有一个终点,除了没有k/σ提供数据