钢筋混凝土板的拉伸硬化过程分析

R. Ian Gilbert

摘 要：混凝土的抗拉能力在计算钢筋混凝土梁或板的强度时通常被忽视,尽管具体的拉应力继续进行，由于拉钢筋到混凝土之间裂缝的转换力量。这一种混凝土的拉力被称为混凝土的张力硬化。在开裂后它会影响钢筋混凝土的刚度，因此它的挠度和裂缝宽度必须根据屈服强度负载。对轻混凝土，例如楼板，全部裂缝的弯曲刚度比没有裂缝部分的要小很多，张力加劲有助于刚度。在本文中，ACI方法必须考虑到紧张加劲，欧洲和英国的方法是严格评估和预测与实验结果进行比较。最后，建议依据钢筋混凝土楼板的建模张力加劲设计控制偏转。

关键词：开裂，蠕变挠度，混凝土，钢筋，适用性，收缩，混凝土砖。

1.引言

由于拉钢筋到混凝土之间裂缝的转换力量，拉伸能力在计算时通常忽略钢筋混凝土梁或板的强度,尽管具体的拉应力将持续。这一种混凝土的拉力被称为张力硬化,它会影响各部分的刚度，因此必须考虑其挠度和裂缝宽度。

随着高强度钢筋的运用，增强混凝土板通常使用相对少量的拉钢筋，经常接近相关建筑法规允许的最低允许值。对于这样的构件，弯曲完全开裂的一个截面刚度比未开裂的截面小许多倍，张力加劲大大促进了开裂后构件的刚度。在设计中，挠度和裂缝的控制通常是在屈服水平调整考虑的，并在开裂后刚度的建模精确是必需的。

挠度计算中最常用的方法包括确定破解构件平均有效的转动惯量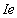（）。几种不同的经验公式可用于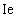，包括著名的方程开发Branson（1965）和ACI 318（ACI 2005）。其他的张力硬化模式包括在Eurocode 2（CEN1992)和（British Standard BS 8110 1985），最近，Bischoff（2005）表明，布兰森的方程对含有少量的钢筋混凝土构件钢筋平均刚度评估过高，他提出了一个对于的替代方程，这基本上是与Eurocode 2方案兼容。

在本文中，包括张力加劲在内的各种方法在混凝土结构设计，包括在Eurocode 2，ACI 318，BS8110模式，批判性进行评估经验预测与实测挠度进行了比较。最后，模拟张力加劲的建议结构设计均被包括在内。

2.开裂后弯曲响应

考虑一个简支负载的变形响应，钢筋混凝土板如图1所示。在负载小于开裂负载的情况下，，该构件未开裂和表现均匀的弹性，以及挠度斜率是成正比的未开裂的转动惯量的换算界面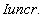，。该构件的第一裂缝在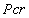当极端纤维在混凝土拉应力的最大部分到达混凝土弯拉强度破裂或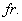时。

有一个刚度突变，并立即出现裂纹。在包含了破碎的部分，抗弯刚度显着下降，但大部分仍然未开裂的梁，随着负载的增加，出现更多的裂缝形式和整个构件的平均抗弯构件减少。

如果在梁的混凝土开裂区域内施加拉力而没有压力，负载变形关系将遵循虚线ACD，如图1。如果平均极端纤维拉伸应力在混凝土开裂后留在fr，将遵循虚线AE。事实上，实际的反应是介于这两个极端自建，如图1所示为实线AB型。实际反应之间的区别和零张力反应的张力是加强效应。

随着越来越多的裂缝发展和实际响应趋向于零紧张反应，一般的拉应力混凝土减少，至少要等到裂缝模式充分开发和裂缝的数量趋于稳定。对于含有少量的拉结钢筋砖（通常= As/bd0.003），紧张硬化可能超过50％的钢筋混凝土的刚度破坏屈服加载而且仍然要达到和超过的钢产量和负荷接近极限地步。依据在长期挠度的计算下，可能是由于综合作用的拉伸蠕变、蠕变断裂,收缩开裂，在持续负载下张力加劲效应随着时间而减少。

3.加劲的张力模型

梁的弯曲或板在使用载重挠度可以瞬间从弹性论计算通过混凝土弹性模量Ec和有效的惯性矩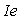。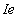的价值对于构件是计算使用Eq.[1]计算公式为一个在跨中简支构件和加权平均计算价值在正，负弯矩区的一个连续的跨度。

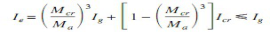                            （1）

为破碎的换算截面的惯性矩；

为总截面的质心轴的惯性矩，但更正确的应该是换算截面的未开裂的惯性矩；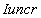

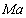为在构件的最大弯矩阶段的计算挠度；

为开裂力矩（=）；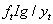

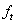为混凝土断裂模数；

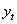为从质心的距离轴的毛截面的纤维在极端的张力。

ACI方法的修改包括在澳大利亚标准AS3600-2001(AS2001)解释的收缩引起的张力可能会显著的降低混凝土的开裂构件这个事实。开裂的构件由公式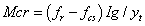决定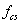，是纤维在最大收缩引起的拉在未开裂截面应力在极端的情况发生开裂（Gilbert 2003）。

Eurocode 2（1994）

这种方法涉及到在特定的曲率计算交叉部分，然后结合取得的挠度。开裂后曲率K的计算为 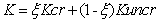                                             (2)

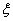为分配系数占目前水平和打击的程度，并给出

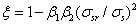                                   （3）

为变形钢筋=1.0，光圆钢筋=0.5；

为单一的，短期负荷为1.0，重复或持续荷载为0.5；

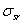在应力加载造成的受拉钢筋首先开裂，计算混凝土张力；

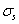是考虑钢筋的加载应力；

为忽略应力混凝土的曲率部分；

曲率的未开裂换算截面。

在纯弯曲的板，如果抗压混凝土和钢筋都是线性和弹性，  等于 ，结合公式1和2能得          （4）

对于一个包含变形钢筋受弯构件在短期的加载，公式3和公式4可以重新安排，以提供下列替代表达式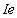短期挠度[最近提出Bischoff(200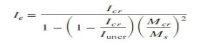5)]

                            (5)

这种做法，目前在英国已经取代了Eurocode 2的方法，还涉及到在特定的截面曲率的计算，然后结合获得的挠度。开裂后的曲率K计算假设（1）、平面为平截面；（2）、压缩的钢筋混凝土被认为是线弹性；（3）、凝固的混凝土应力分布是三角形的，在中性轴和一个值为零值在1.0 MPa的瞬间强度钢质心，减少至0.55MPa。

4.与实验数据的比较

为了测试ACI 318，欧洲规范的适用性和BS 8110轻型钢筋混凝土构件的方法，测量的力矩与11简支的挠度反应相对，单钢筋单向拉伸板含钢量计算结果在范围进行比较，该板块（指定S1至S3，S8的，到SS2的SS4型，和Z1到Z4）都是柱状，矩形截面，850mm，并在一个有效深度载有纵向拉伸单层钢筋d(Es=200000MPa和屈服应力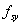=500MPa)。每个板块的详细情况见表1，包括有关的几何和材料特性。

在每个板跨中挠度的预测结果与实测时，在跨中力矩等于1.1，1.2和1.3Mcr列出在表2。与瞬时变形响应的测量力矩的两跨中的板。（SS2 and Z3）进行比较和计算结果获得图2，使用三个代码方式同时显示的结果，如果没有出现开裂，如果张力加劲被忽略。

5.讨论结果

很明显，这些轻型钢筋板，张力加劲非常显著，提供一个大比例的开裂后刚度。从表2，跨中挠度的比例得到了加劲，对测量张力跨中挠度忽视（在Mcr和1.3Mcr范围）是在1.38-3.69范围，取平均值2.12。也就是说，平均而言，张力加劲超过50％的一个轻型钢筋板在屈服荷载的瞬间开裂。

对于每一个板，在ACI 318的方法低估了瞬间挠度后开裂，特别是对于轻型钢筋板。此外，在这一时刻ACI 318突然不成模型，在起初开裂处，突然改变力矩偏转结果的方向，也没有预测的正确形状矩挠度曲线。

在短期挠度的低估使用ACI 318模式是经化验报告在这里在表示实践中相当大的比。不同于Eurocode 2和BS 8110，ACI 318模型不承认或为在开裂的力矩，这将不可避免地减少在实践中出现的由于张力引起的混凝土干燥收缩或热变形。对于许多板，因早期干燥或温度变化在数周内将发生铸件的开裂，以及经常暴露之前，其板全方位服务的负荷。

通过限制混凝土拉伸应力水平的拉伸筋只有1.0 MPa，BS 8110的方法对测试板的上下挠度和立即高于开裂力矩的高估。由于约束的早期收缩和热变形，这并非不合理和占损失的刚度发生在实践中。不过，BS 8110提供了一个相对较差模型刚度，并错误地认为，平均拉力混凝土裂缝进行了实际调高M增大和中性轴的上升。因此，BS 8110开裂后力矩偏转斜率图甚至超过了所有板测量斜坡。这种方法使用比Eurocode 2或ACI两种方式更繁琐。

在所有情况下，Eurocode 2挠度计算[EPS.(3)-(5)]是在更接近与实测挠度在整个负载范围内协议。可以看出在图2，荷载—挠度曲线的形状并使用Eurocode 2是一个比这更好的代表性实际曲线结果，使用EP.(1)。考虑到具体的变异材料性能影响的板，该协议Eurocode 2在运行特征和对开裂的随机性之间的预测和试验结果在如此广泛的受拉钢筋比率是相当显著的。在图2（）0.80和1.39之间的值平均值为1.07，Eurocode 2的方法提供了ACI 318或BS 8110更好地估计短期行为。

6.结论

虽然张力加劲只对重钢筋梁挠度的影响相对较小，这是非常重要的对于Iuncr / ICR的比例很高的轻型钢筋构件，例如作为最实用的钢筋混凝土楼板。加劲张力的模型纳入ACI(2005)，Eurocode 2(CEN1993)，和BS 8110(1985) 已提交并且轻型钢筋混凝土楼板的适用性已进行评估。计算模型的三个代码瞬时挠度进行了比较与来自11个实验室测试测量挠度在含有不同数量的钢筋板。在Eurocode 2方案EP.(5)已被证明是更准确地模拟了瞬时负载变形的加固构件轻型钢筋构件的波形和ACI 318（EP.(1)比更为可靠的方法。

出自：JOURNAL OF STRUCTURAL ENGINEERING © ASCE / JUNE 2007

参考文献

[1]American Concrete Institute （ACI）.（2005）. “Building code requirements for structural concrete.” ACI 318-05, ACI Committee 318, Detroit.

[2]Bischoff, P. H. (2005). “Reevaluation of deflection prediction for concrete beams reinforced with steel and fiber-reinforce polymer bars.” J.Struct. Eng., 131(5), 752–767.

[3]Branson, D. E. (1965). “Instantaneous and time-dependent deflections ofsimple and continuous reinforced concrete beams.” HPR Rep. No. 7,1, Alabama Highway Dept., Bureau of Public Roads, Ala.

[4]British Standards Institution (BS).（1985）. “Structural use of concrete, Part 2, code of practice for special circumstances.” BS8100: Part2:1985, British Standard, London, England.

[5]European Committee for Standardization（CEN）. （1992）. “Eurocode 2:Design of concrete structures Part 1-1: General rules for buildings.”DD ENV 1992-1-1, European Prestandard, Brussels, Belgium.

[6]Gilbert, R. I.（2003）. “Deflection by simplified calculation in AS3600-2001—On the determination of fcs.” Australian J. Structural Engineering,5（1）, 61–71.

[7]Standards Australia（AS）. （2001）. “Australian standard for concrete structures.”AS 3600-2001, Sydney, Australia.JOURNAL